8.3 Приклади розв'язання задач

Приклад 8.1. На навантаженні присутні падаюча та відбита хвилі

,

_пад = 0,349 рад, _від = 0,393 рад. Розрахувати коефіцієнт відбиття навантаження, зсув фази відбитої складової відносно падаючої і коефіцієнт стоячої хвилі. Записати комплексний коефіцієнт відбиття на відстані від навантаження l /  = 1,6.

 Використовуємо прості формули (8.1), (8.2), (8.8): ,

_н = 0,393 – 0,349 = 0,044 рад = 2,5, КСХ = , _ = 0,044 – 4·π·1,6 =

= – 20,062 = 8 – 20,062 = 5,071 рад, . 

Приклад 8.2. Продовження прикладів 6.3, 8.1. Знайти значення падаючої, відбитої та прохідної потужності.

 В прикладі 6.3 знайдено падаючу потужність Р_пад = 1474,3 мкВт, а в прикладі 8.1  коефіцієнт відбиття . Відбита потужність Р_від = = =м0,111²1474,3 = 18,2 мкВт. Відповідно до (8.3) прохідна потужність

Р_прох = 1474,3 - 18,2 = 1456,1 мкВт = 1,46 мВт. 

Приклад 8.3. В лінії передачі коефіцієнт відбиття = 0,58. Знайти екстремальні значення нормованих стоячих хвиль і КСХ.

В максимумі стоячої хвилі нормоване значення дорівнює E_max = 1 + = =л1,58, в мінімумі  E_min = 1 - = 0,42. За формулою (8.7) або (8.8) коефіцієнт стоячої хвилі КСХ = 3,76. 

Приклад 8.4. Розрахувати нормовані значення опору навантаження і вхідного опору на відстані l = 0,611 в лінії передачі з хвильовим опором 50 Ом при: а) Z_н = 9 + i90 Ом; б) Z_н = 0; в) Z_н = .

 Нормовані значення опору навантаження розрахуємо за формулою (8.10):

а) , разів.

На відстані l від навантаження повний вхідний опір (8.19) знаходимо за допомогою, наприклад, програми MathCAD

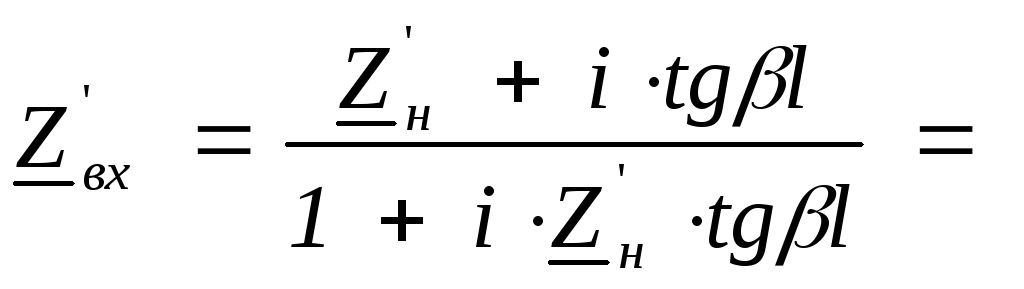1,09 – i4,867;

б) в режимі короткого замикання вхідний опір, як видно з (8.24), носить чисто реактивний характер, тому . В заданому перерізі вхідний опір носить індуктивний характер;

в) в режимі холостого ходу вхідний опір, як видно з (8.25), носить чисто реактивний характер, тому . В заданому перерізі вхідний опір носить ємнісний характер. 

Приклад 8.5. На рис. 8.4,а зображена еквівалентна схема вхідного кола транзистора НВЧ, який використовують в генераторах із зовнішнім збудженням. Значення елементів еквівалентної схеми R₁ = 5,5 Ом, L₁ = 6,5 нГн. Вважаючи вхід транзистора навантаженням несиметричної стрічкової лінії з хвильовим опором, заданим в прикладі 7.5, визначити на частоті 0,98 ГГц : а) відстань від навантаження, на якій вхідний опір буде чисто активним; б) відстань від навантаження, на якій активна складова вхідного опору дорівнює хвильовому опору.

 Спочатку знаходимо вхідний опір навантаження (табл. 8.1)

,

або в нормованому вигляді , рази. Далі використовуємо формулу (8.19). Оскільки l = 2l /  = 2l^', то вхідний опір

;

а) необхідно забезпечити =0. Розв'язок знаходимо за допомогою, наприклад,

п рограми MathCAD. Розв'язання трансцендентного рівняння =0

дає l^' = 0,422. Раніше (див. приклад 7.5) знайдено розміри несиметричної стрічкової лінії w/h = 0,5065 для  = 7,4. За формулою (7.21) розраховуємо ефективну діелектричну проникність _еф = 4,903.

Довжина хвилі в необмеженому просторі  = 30,61 см, а довжина хвилі в лінії передачі без дисперсії (табл. 6.1) = 13,83 см.

Відповідно l = l^' = 0,42213,83 = 5,83 см;

б ) має бути . Розв'язання трансцендентного рівняння

дає l^' = 0,134. Відповідно l = l^' = 1,86 см.

Якщо потрібно знайти відстань від навантаження, на якій активна складова вхідної провідності дорівнює хвильовій провідності, розв'язується рівняння .

Приклад 8.6. До основної лінії передачі без дисперсії, яка має хвильовий опір Z_Х1 = 50 Ом, послідовно підключений відрізок лінії з хвильовим опором Z_Х2 завдовжки l₂ = ₂/4, навантажений на активний опір R_н2 = 8 Ом. Заповнення повітряне. Знайти значення Z_Х2, при якому на частоті f₀ = 5 ГГц в основній лінії буде режим біжучої хвилі. Розрахувати залежність коефіцієнта відбиття від частоти.

 Умова рівності нулю коефіцієнта відбиття випливає з (8.20), (8.21) і набуває вигляду, тобто дорівнює нулю тоді, коли повний вхідний опір чвертьхвильового відрізка є чисто активним і рівним хвильовому опору основної лінії передачі. За формулою (8.23) вхідний опір .

З рівняння знаходимо .

Частотну залежність коефіцієнта відбиття розрахуємо за допомогою формули (8.20) з підстановкою загальної формули (8.17)

, де l₂ = ₂/4 = 15 мм.

Н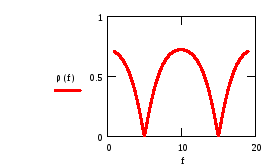 а рис. 8.3 зображені відповідні графіки, побудовані в широкій і у вузькій смугах

Рисунок 8.3  Залежність коефіцієнта відбиття від частоти

в широкій і вузькій смугах частот 

частот. Видно, що із зростанням частоти коефіцієнт відбиття періодично змінюється, досягає нульових значень на частотах, на яких довжина чвертьхвильового трансформатора набуває значення l₂ = k₂/4, де k = 1, 3, 5, …  непарне число. У вузькій смузі частот характеристику іноді називають V-подібною через відповідний вигляд.