
Матричные уравнения
A-1|AX=В→ EX=A-1B→ X=A-1B
A – матрица коэффициентов, X – столбец неизвестных.
11.
Системы n уравнений
X=A-1B= =
=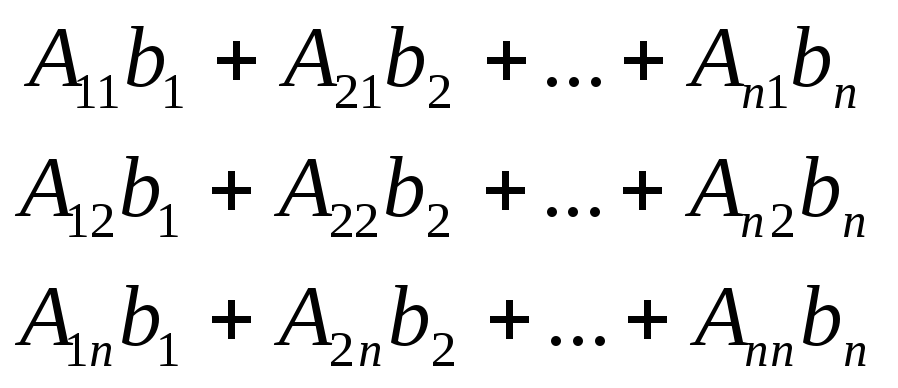
12.
Формула Крамера.
![]() ,
Δi-определитель
полученный из матрицы А если в ней
столбец заменить на столбец свободных
членов. Вывод
,
Δi-определитель
полученный из матрицы А если в ней
столбец заменить на столбец свободных
членов. Вывод
Теорема Крамера.
Система из n линейных уравнений м n неизвестными, определитель которой отличен от 0, имеет единственное решение, которое может быть найдено по формуле Крамера.
13.
Минор матрицы
Ранг матрицы
-
Если в матрице А выделить k строк и k столбцов, то определитель составленный из элементов, стоящих на пересечении этих строк и столбцов называется минором k-го порядка матрицы А. Ранг матрицы – наивысший порядок минора отличный от 0
-
Элементы S1, S2…Sn называются линейно зависимыми, если существует набор чисел n1, n2…nn такой что n1S1+n2S2+…+nnSn=0 и хотя бы одно из чисел ni≠0. Если это выполняется при всех т=0, то элементы называются не линейно зависимыми. Ранг матрицы – количество линейно независимых строк или столбцов этой матрицы.
14.
Теорема Кронехера-Копелли
Система из m линейных уравнений с n неизвестными совместна тогда и только тогда, когда ранг матрицы А равен рангу расширенной матрицы, причем:
-
если rA=rÂ=n – 1 решение.
-
если rA=rÂ<n - ∞ решений.
-
если rA≠rÂ≤n - нет решений.
16.
Совместная система – система, имеющая хотя бы 1 решение.
Решение системы – набор чисел такой, что при подстановке в систему каждое уравнение превращает в равенство.
Общее решение – решение из которого можно получить все частные решения
1. Все неизвестные выражаются через 1 параметр (кол-во неизвестных = n-rA)
2. Все базисные неизвестные выражаются через свободные члены.
Свободное неизвестное – неизвестное в ответе, остальные – базисные
Алгоритм Гаусса
-
Найти ai1≠0 и поставить на первое место
-
S1→S1:a11
-
Si→Si-ai1S1, где i=2,3...m
-
Ищем aj2≠0(j≠1) и т.д. если aj2=0 при любом j=2…m, то ищем aj3≠0 (j≠1).
18.
Операции над векторами и их свойства
-
Сложение
А)![]()
Б)
![]()
В)
![]()
Г)
![]()
Противоположные вектора – вектора модули которых равны, но направление противоположное.
19.
-
Умножение вектора на число
![]() ,
если а)
,
если а)
![]()
Свойства
1.
![]()
2.
![]()
3.
![]()
![]()
4.
![]()
Орт вектора – единичный вектор сонаправленный с данным вектором.
20.
О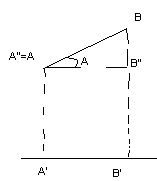 сь
– прямая с заданным направлением.
сь
– прямая с заданным направлением.
Проекция точки – основание перпендикуляра, опущенного из точки на ось.
ПрeAB=|AB| или -|AB|
Свойства проекции.
1. ПреAB=|AB|cosA
Доказательство: 1. A-острый Из треуг. ABB’’: |AB’’| =|AB|cosA
2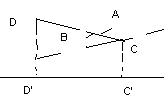 .
A-тупой B=180-A
|CC’|=|DC|cosB=|DC|cos(Pi-A)=-|DC|cosA =>
.
A-тупой B=180-A
|CC’|=|DC|cosB=|DC|cos(Pi-A)=-|DC|cosA =>
=>|D’C’|=-|DC|cosA
2. ПреAB+ПреВС=Пре(АВ+ВС)
Д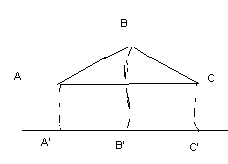 оказательство:
оказательство:
1.А1-угол между AB и e A2 – угол между ВС и е острые
ПреАВ=|А’В’| ПреВС=|В’С’ | Пре(АВ+ВС)=|В’С’|+|А’В’| =|A’C’|
2.А1- острый A2 – тупой
ПреАВ=|А’В’| ПреВС=-|В’С’ | Пре(АВ+ВС)=|В’С’|-|А’В’| =|A’C’|
3.k*Прea=Преka
Доказательство:
1. K>0 => ka||a => угол не меняется
Преа=|a|cosA Преka=|ka|cosA=|k|Преа
2. K<0 => угол между ka и e =Pi-A
Прeka=|ka|cos(Pi-A)=|k||a|(-cosA)=-|k||a|cosA=kПрea
21.
ab=|a||b|cosA
Свойства
1. Преа=|a|cosA=ab/|b|
Праb=|b|cosA =>ab/|a|
=>ab=|b|Прba=|a|Праb
2. a(b+c)=ab+ac
Доказательство: ab=|a|Прab ac=|a|Прас
Пра(b+c)=Праb +Прас =>|a|Pra(b+c)=|a|Prab+|a|Praс => a(b+c)=ab+ac
3. (na)b=a(nb)=n(ab)
Доказательство: a(nb)=|a|Prabn=|a|nPrab=n(ab)
4. Два ненулевых вектора а≠0, b≠0 перпендикулярны когда ab=0 и наоборот.
Доказательство: 1. если a┴b, то угол A=90o => cosA=0 , то ab=0
5. Связь между длиной вектора и скалярным произведением.
Aa=|a||a|=|a|2=>
|a|=![]()
22.
c=axb, если
-
|c|=|a||b|sinA
-
c┴a c┴и
-
a b с образуют первую тройку векторов
Свойства
-
геометрический смысл S=axb
-
axb=-bxa
-
ax(b+c)=axb+cxa
-
Умножение вектора на число (na)xb=ax(nb)=n(axb)
23.
Смешанное произведение векторов
C(axb)=a(bxc)=abc
V=abc
24.
Признак коллинеарности векторов
a\\b то существует k≠0? Что b=ka
Доказательство:
-
Если b=ka =>b||a, по определению умножения вектора на число.
-
Пусть b||a , возьмем k=|b|/|a|
Если а||b то k=|k|
Если a||b то k=-|k|
Тогда с=ka будет с=b, т.е. b=ka, c=ka
-
|c|=|k||a|
-
c||a
-
c||a, если k>0
-
c||a, tckb k<0
Теорема.
Если 2 вектора коллинеарные то они линейно зависимы.
Доказательство:
По признаку коолинеарности: a=kb a-kb=0
-
a≠0, b≠0 тогда a и b ЛЗ l1=1, l2=-k
-
а=0, тогда l1=1, l2=0 – ЛЗ
Два ненулевых вектора а≠0, b≠0 перпендикулярны когда ab=0 и наоборот.
Доказательство: 1. если a┴b, то угол A=90o => cosA=0 , то ab=0
3 вектора компланарны если лежат в одной плоскости т.е. их смешанное произведение равно 0.
25.
Векторы a1 a2…an называются ЛЗ если существуют n1 n2…nn, где хотя бы одно ni≠0, что n1a1+n2a2+…+annn=0, если это условие выполняется при всех n=0 то векторы ЛНЗ
Базисом в некотором пространстве называется набор из n ЛНЗ векторов a1 a2…an, такой что любой вектор b из этого пространства можно представить как линейную комбинацию базисных векторов т.к. существуют числа n1 n2…nn b=n1a1 +n2a2+…+nnan
26.
Теорема.
Если 2 вектора коллинеарные то они линейно зависимы.
Доказательство:
По признаку коолинеарности: a=kb a-kb=0
-
a≠0, b≠0 тогда a и b ЛЗ l1=1, l2=-k
-
а=0, тогда l1=1, l2=0 – ЛЗ
В соответствии с этой теоремой получаем что если вектора неколлинеарны то они ЛНЗ.
28.
Декартовая система координат в пространстве
i j k – базис ДС
1. |i|=|j|=|k|=1
2. i┴J┴k
3. i j k –правая тройка тогда k=ixj
32.
axb= ixj=k ixk=-j jxi=-k jxk=I kxj=-I kxi=j
ixj=k ixk=-j jxi=-k jxk=I kxj=-I kxi=j
38.
Уравнение плоскости через точку
A(x-x0)+B(y-y0)+C(z-z0)=0
Общее уравнение
Ax+By+Cz+D=0
39.
Пересечения с осями
Ox- x=-D/A
Oy- y=-D/B
Oz- z=-D/C
ABC-наклон D-сдвиг
-
D=0 Проходит через н.к.
-
A=0 Не пересекает ох
-
А=0, Д=0 Плоскость проходит через ox
-
A=0, B=0 плоскость параллельна плоскости Oxy
40.
Уравнение плоскости в отрезках
![]()
![]()
42.
Расстояние от точки до плоскости
![]()
43.
Взаимное расположение плоскостей
1. α2||α1
если N1||N2
![]()
2. α2┴α1 Если N1N2=0 A1A2+B1B2+C1C2=0
3. Угол между плоскостями – угол между N1 и N2
46.
Каноническое уравнение прямой Параметрические уравнения прямой
![]()
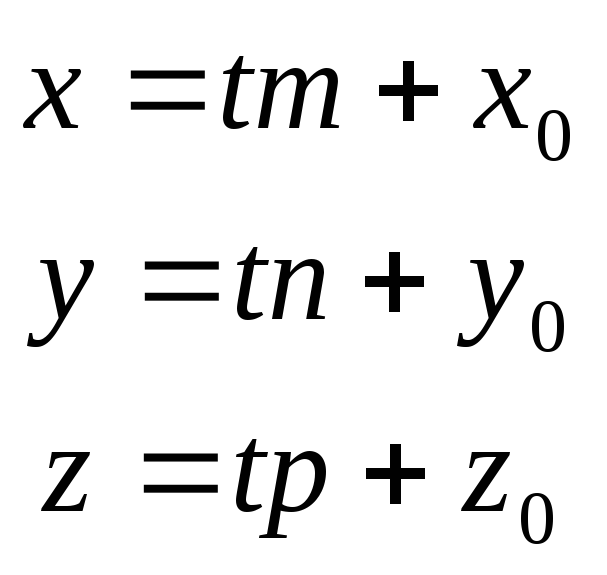
47.
Прямая на пересечении 2 плоскостей.
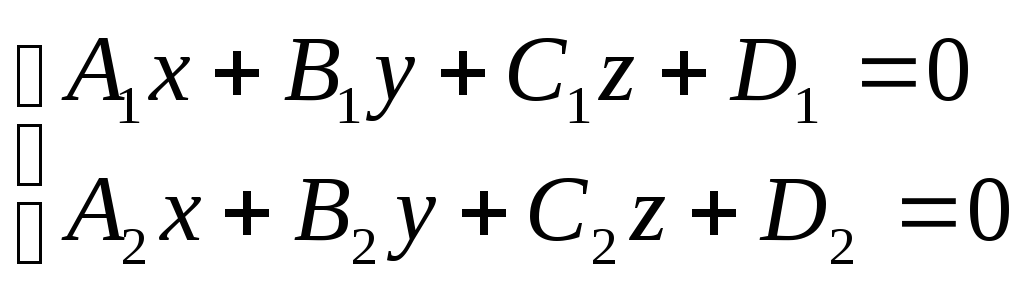 D1 не равно D2
D1 не равно D2
48.
![]()
49.
1. l1||l2
если S1||S2
=>
![]()
2. . l1┴l2 если S1┴S2 =>S1S2=0 =>m1m2+n1n2+p1p2
Угол между прямыми
cosA=![]()
Направляющие косинусы прямой – косинусы направляющего вектора.
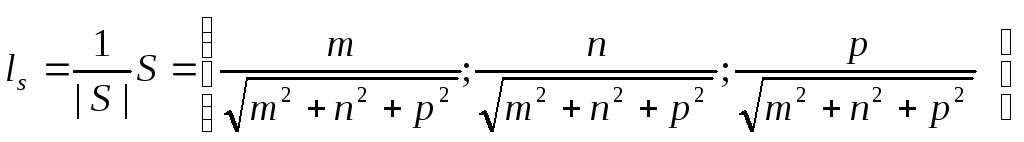
50.
Р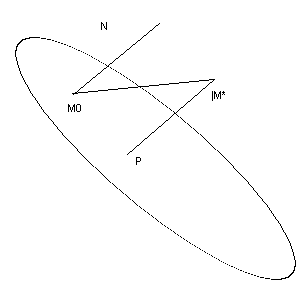 асстояние
от точки до прямой.
асстояние
от точки до прямой.
P – проекция M*
M*P||N
D=|M*P|=|PrNM0M|=|N*M0M|/|N|=
=![]() =
=
=![]()
51.
Угол между прямой и плоскостью
![]()
Расположение прямой и плоскости.
-
l||α => SN=>NS=0 Am+Bn+Cp=0
-
l┴α => S||N =>
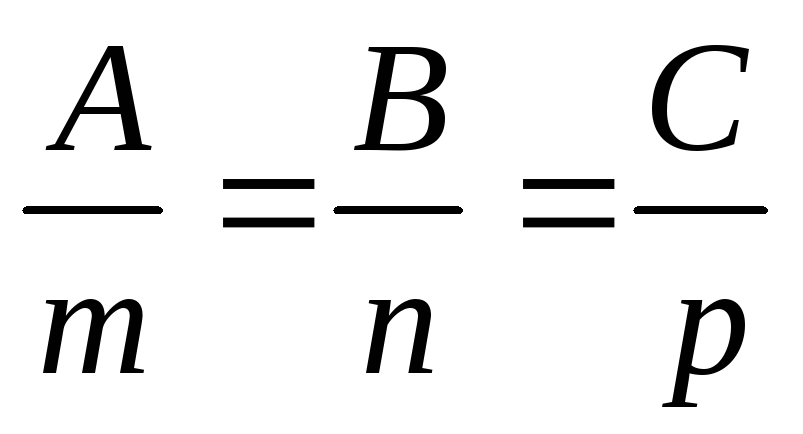
52.
П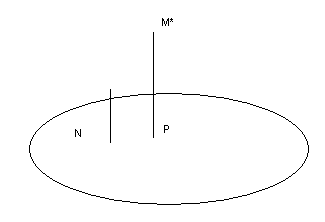 роекция
точки на плоскость
роекция
точки на плоскость
α: Ax+By+Cz+D=0
l: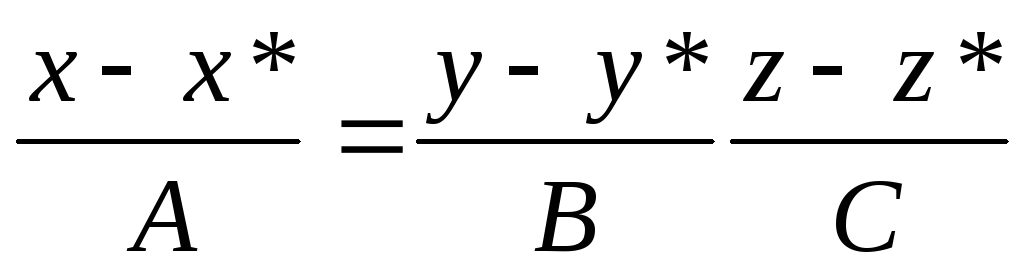
x=x*+At
y=y*+Bt
z=z*+Ct
подставляем в α: и получаем
![]()
П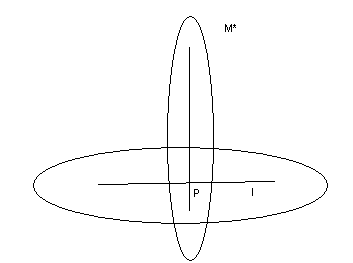 роекция
точки на прямую
роекция
точки на прямую
l: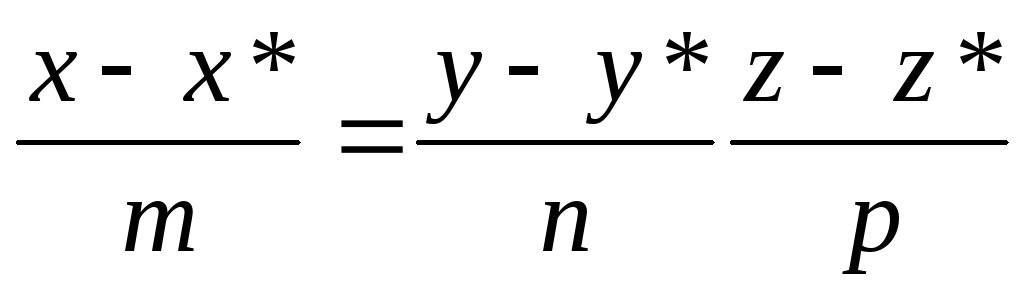
l ┴α: m(x-x*)+n(y-y*)+p(z-z*)=0
x=x*+At
y=y*+Bt
z=z*+Ct
![]()
53.
Проекция прямой на плоскость.
