2.2.3 Алгоритмы циклической структуры

Определение. Алгоритмом циклической структуры называется алгоритм, в котором предусмотрено выполнение одной и той же последовательности действий.

Определение. Алгоритм, содержащий цикл, называется циклическим.

Циклический алгоритм позволяет существенно сократить объем программы.

Циклом называется многократное выполнение последовательности операторов с различными входными данными на каждом шаге цикла.

Циклы подразделяют:

• циклы с известным числом повторений (параметрические циклы или циклы со счетчиком);

• циклы с неизвестным числом повторений (итерационные циклы).

Определение. Параметрическим называется цикл, число повторений тела цикла подсчитывается с помощью специальной переменной (параметра цикла), для которой известны начальное и конечное значения, шаг ее изменения.

Определение. Итерационным называется цикл, число повторений которого заранее неизвестно, но может быть определено в ходе его работы.

Правила организации цикла

1. Подготовка цикла. Перед началом цикла параметру цикла присваивается начальное значение;

2. Тело цикла. Действия, повторяемые в цикле для различных значений параметра цикла.

3. Модификация. Внутри тела цикла параметр цикла увеличивается на шаг изменения параметра цикла перед каждым новым его повторением.

4. Управление циклом. Осуществляется: проверка условия продолжения или окончания цикла, переход на начало тела цикла, если выполняется условие продолжения цикла или выход из цикла по его окончании.

Определение. Параметром цикла называется переменная, значение которой изменяется на некоторую величину на каждом шаге цикла. Шаг изменения параметра может быть величиной постоянной или переменной.

Цикл с параметром

• цикл по возрастающим значениям параметра;

• цикл по убывающим значениям параметра.

1) Алгоритмическая конструкция по возрастающим значениям параметра

где I – параметр цикла;

N1, N2 - его начальное и конечное

S

значение;

S – простой или составной

оператор (тело цикла).

Примечание. N1 изменяется с шагом +1

2) Алгоритмическая конструкция по убывающим значениям параметра:

обозначения прежние

S

Примечание. N2 изменяется с шагом -1.

Пример 1.

Вычислить сумму: S=1² + 2² + 3² + … + n² = , где n – заданное число.

N S = 0 S = S + i2

Алгоритм решения задачи 1. Начало 2. Ввести N 3. S = 0 (обнуление ячейки суммы) 4. Организуем цикл по I, присваиваем I нач.знач. и кон.значение 5. Вычислить i2 и прибавить к текущему значению S (обозначение S = S + i2) 6. Увеличить i на 1 (обозначение i = i +1) 7. Сравнить i с n, если I < N, то вернуться к п.5, иначе перейти к п.8 8. Вывести S. 9. Конец. Основная повторяющаяся операция: S = S + i2 выполняется при различных значениях i. Величина i называется параметром цикла. Параметр цикла изменяется от нач.значения i=1 до конечного i=n с шагом 1.

Цикл с предусловием

Действие цикла

1. Вначале вычисляется значение выражения B.

2. Если B = true, то выполняется оператор S, и снова происходит возврат на вычисление B.

Так повторяется до тех пор, пока B не будет false, что является выходом из цикла. Если первоначальное значение B есть false, то цикл не выполнится ни разу.

Пример 2. Условие прежнее (Вычислить сумму: S=1² + 2² + 3² + … + n² = , где n – заданное число)

S = 0 i = 1 S = S + i2 I = I + 1 i = i+1

Алгоритм решения задачи 1. Начало 2. Ввести n 3. S = 0 (обнуление ячейки суммы) 4. Положить i =1 (нач.значение) 5. Открываем цикл по I 6. Сравниваем I с N. Если I>N, переход к п.10, иначе 7. S = S + i2 8. i = i +1 9. Переход к п.6 10. Вывести S. 11. Конец.

Цикл с постусловием

Действие цикла

1. Выполняются операторы S.

2. Вычисляется значение выражения В. Если В = false, то снова выполняются операторы S и т.д. Повторение продолжается до тех пор, пока В не примет значение true, которое является завершением цикла. Если с самого начала В = true, то операторы S выполняются одни раз.

3. Выход из цикла осуществляется при истинности (!) некоторого логического выражения.

Пример 3. Условие прежнее (Вычислить сумму: S=1² + 2² + 3² + … + n² = , где n – заданное число)

N S = 0 i = 1 S = S + I2 I = I +1

Алгоритм решения задачи 1. Начало 2. Ввести n 3. S = 0 (обнуление ячейки суммы) 4. Положить i =1 (нач.значение пар.цикла) 5. Организуем цикл по I 6. Вычислить S = S + i2 7. i = i +1 8. Сравнить i с n, если I >N, то вернуться к п.6, иначе перейти к шагу 9. 9. Вывести S. 10. Конец.

Вложенные циклы (сложные)

Вложенными циклами называют такие схемы циклов, когда внутри одного цикла присутствуют от одного и более циклов.

Цикл, содержащий в себе другой цикл, называют внешним.

Цикл, содержащийся в теле другого цикла, называют внутренним.

Внутренний и внешний циклы могут быть любыми из трех рассмотренных видов: циклами с параметрами, циклами с предусловием, циклами с постусловием.

При использовании вложенных циклов нужно соблюдать следующие правила:

• внутренний цикл должен целиком содержаться в теле внешнего;

• если при организации вложенных циклов используются операторы for, то параметры циклов должны быть различными;

• из внутреннего цикла можно в любом месте выйти во внешний цикл; из внешнего цикла можно войти во внутренний только через его заголовок.

• параметр внутреннего цикла изменяется быстрее, чем внешнего цикла.

Сложные циклы условно разбивают на уровни вложенности.

Алгоритмическая конструкция вложенности циклов с параметром

ТЦ 1

ТЦ 2

Внешний цикл 1 имеет уровень 0, внутренний цикл 2 – уровень 1. Цикл 2 является внутренним по отношению к циклу 1.

Возможная глубина вложенности циклов (количество уровней) ограничивается объемом имеющейся памяти ЭВМ.

Параметры циклов разных уровней изменяются не одновременно. Вначале все свои значения изменит параметр цикла наивысшего уровня вложенности (Цикл 2). Затем изменяется на один шаг значение параметра внешнего цикла следующего уровня (Цикл 1) и снова полностью выполняется внутренний цикл и т.д. до тех пор, пока параметры циклов всех уровней не примут все требуемые значения.

Пример.

Таблица Пифагора.

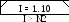
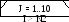
Строки Столбцы