2. Математические модели сигналов.

3. Основные виды зависимостей между переменными.

Для математического описания технологического процесса необходимо вначале установить характер зависимости между переменными величинами. Различают три вида зависимостей между переменными [ ].

1

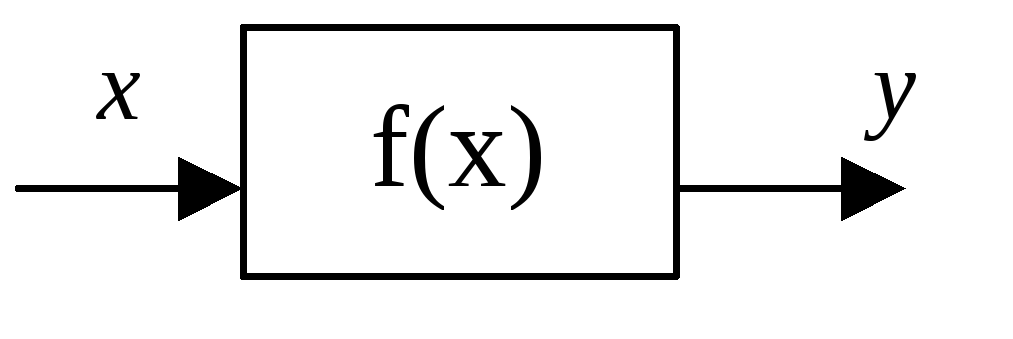
)Функциональная зависимость, например , не содержащая элементов случайностей. В это случае каждому значениюx соответствует определенное значение y. Примером такой зависимости может служить зависимость силы тока от напряждения при постоянном сопротивлении электрической цепи.

2) Зависимость случайной величины  от неслучайной переменной x.

Т

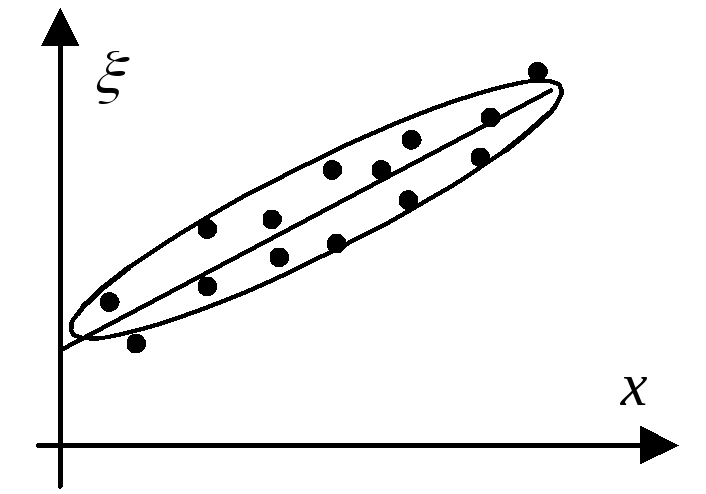
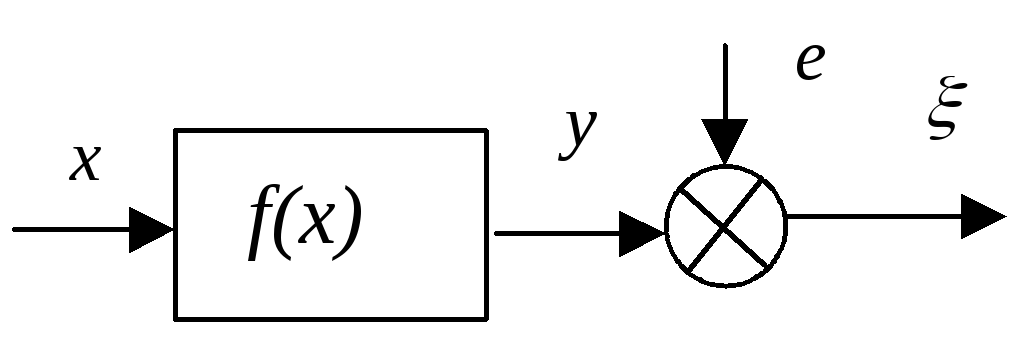акая зависимость имеет место, если выходная переменная измеряется с ошибками или зависит еще от целого ряда фактороввеличина ошибки с параметрами

На графике зависимость имеет вид корреляционного поля. В практике представляет интерес Зависимость условного математического ожидания зависимой переменной от значения аргумента

где - значения выходной переменной при одном и том же значении

- количество параллелных значений выходной переменной при

Данная задача решается методом регрессивного анализа.

3

)Зависимость случайной величины от случайной.В данном случае входные и выходные величины являются случайными по своей сути, т.к. зависят от дополнительных неконтролируемых факторов.

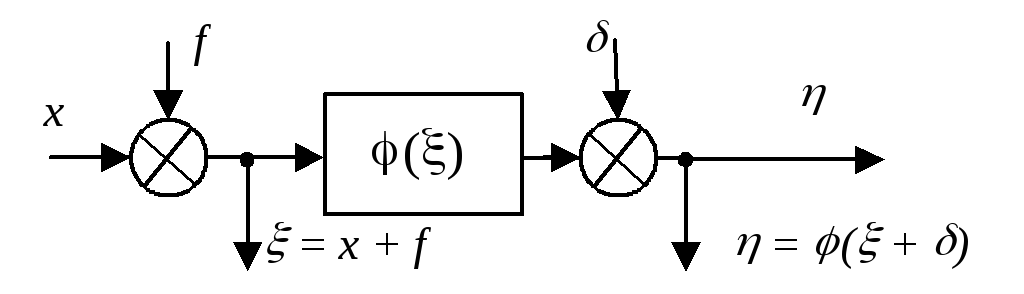
Выходная величина

,

Входная величина , т.е. величинымежду собой некоррелированы.Математическое описание объекта в данном случае представляет собой зависимость условного математического ожидания (среднего) выходной переменной как функции отx, при условии, что входная случайная величина  имеет среднее значение, равное x

Зависимости такого типа изучается методами корреляционного анализа. При этом к вопросам определения вектора коэффициентов методом регрессионного анализа добавляются вопросы исследования тесноты связи.

4. Регрессионный анализ

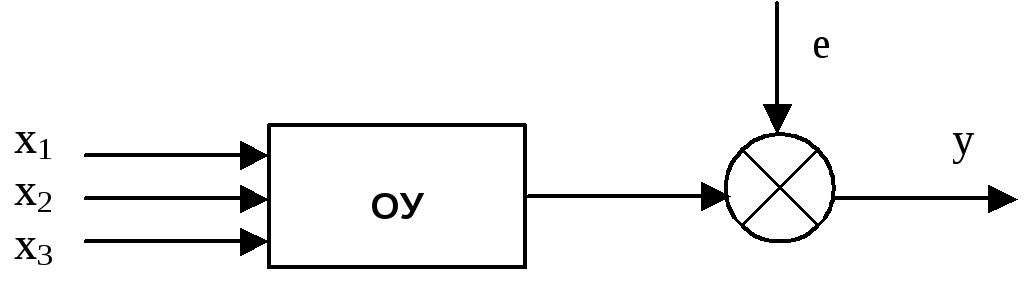
Постановка задачи. Идентифицируется линейный по параметрам объект. Объект описывается линейной математической моделью Выходная величина измеряется с ошибкой. Структурная схема объекта приведена на рисунке. Математическая модель ищется в виде регрессионного уравнения

Регрессионный анализ включает две основные составляющие:

• МНК для оценки вектора коэффициентов;

• дисперсионный анализ для оценки адекватности модели.

Оценки коэффициентов регрессионного уравления получены при выполнении некоторых допущений, которые рассматриваются как предпосылки регрессионного анализа:

• количество экспериментальных данных 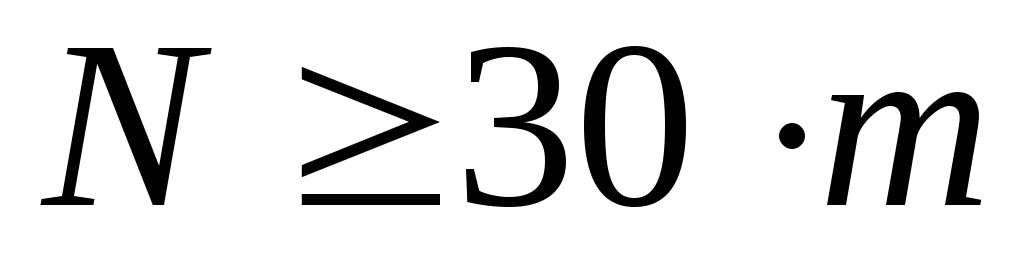; здесьm-количество коэффициентов идентифицируемой модели

• распределение выходной величины yнормальное;

• в процессе эксперимента дисперсия y не изменяется (y стационарно по дисперсии);

• переменная хизмеряется с пренебрежимо малыми ошибками (т.е. детерминирована);

• входные переменные х₁,х₂,х₃стохастически независимы между собой, т. е. коэффициент корреляции между ними равен нулю;

• последующие друг за другом отборы выходной величины не коррелируют между собой

Для выполнения последнего допущения дискретность проведения экспериментов во времени t берется таким, чтобы последовательно взятые y1, y2, y3 были статистически независимы. Для этогоt выбирается больше времени затухания автокорреляционной функции затухания y.

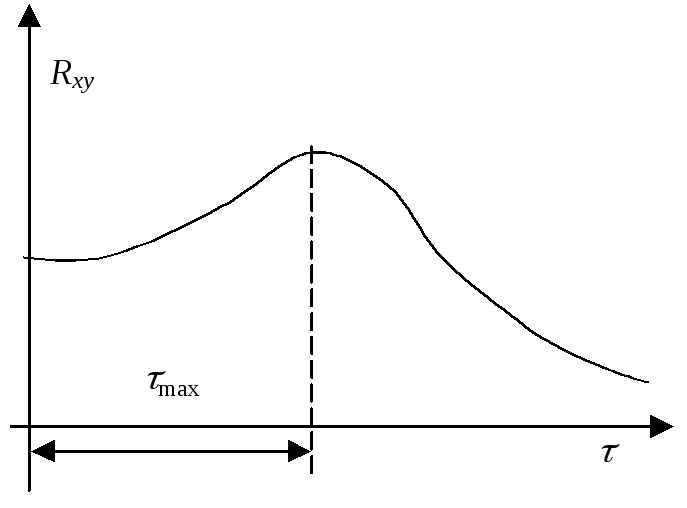
Учет динамики в регрессионном анализе производится в виде транспортного запаздывания между отборамиxиy, которое определяется как время сдвига max взаимнокорреляционной функции относительно оси ординат.

В практике часто пользуются регрессионным анализом и при невыполнении этих допущений, но в этом случае неободимо проверять результаты по дополнительным экспериментам.

Получение оценок МНК для одномерного объекта.

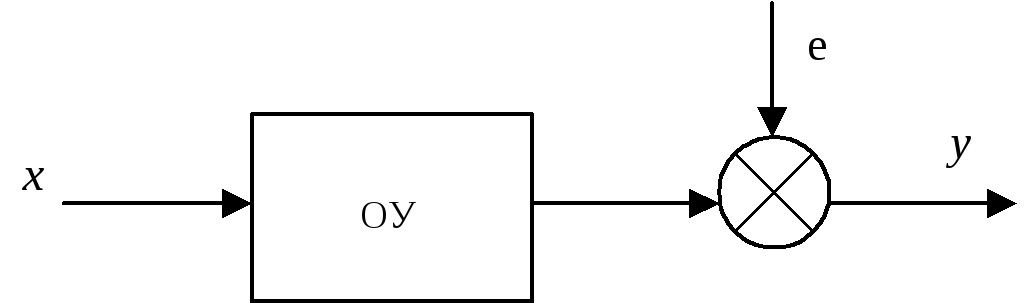
Имеем одномерный объект. Регрессионное уравнение ищется в виде

В процессе эксперимента проводится набор дискретных значенийх_i,y_i. Данные заносятся в таблицу, стороится корреляционное поле зависимости выходной переменной от входной.

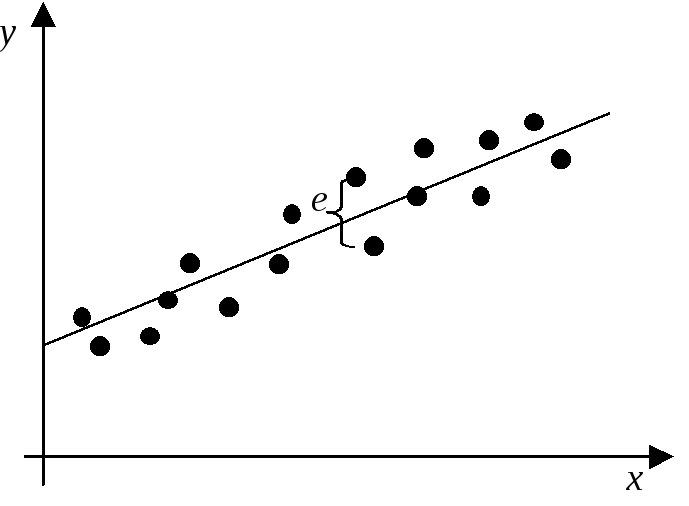
Если бы все точки были на одной прямой, то мы имели бы функциональную зависимость . В результате влияния неконтролируемых входов, что представлено действием помехи, имеем разброс точек вокруг прямой.

Для каждой точки имеется невязк

Формально можно , используя каждую пару точек, получить уравнения прямой, но это множество прямых имеет свои ошибки и каждая прямая не использует всю имеющуюся информацию. Для построения единственной прямой, имеющей минимальную ошибку, используется метод наименьших квадратов (МНК), суть которого нахождение коэффициентов регрессионного уравнения при обеспечении минимальной суммы квадратов отклонений расчетных значенмий выходной переменной от экспериментальных

Использование критерия позволит получить количество уравнений равное количеству коэффициентов. Выведем уравнение для определения коэффициентов одномерной модели:

Введем в выражения критерия МНК выражение модели

Неизвестные b₀,b₁, удовлетворяющие критерию, найдем их из условия равенства нулю производных критерия по коэффициентам модели

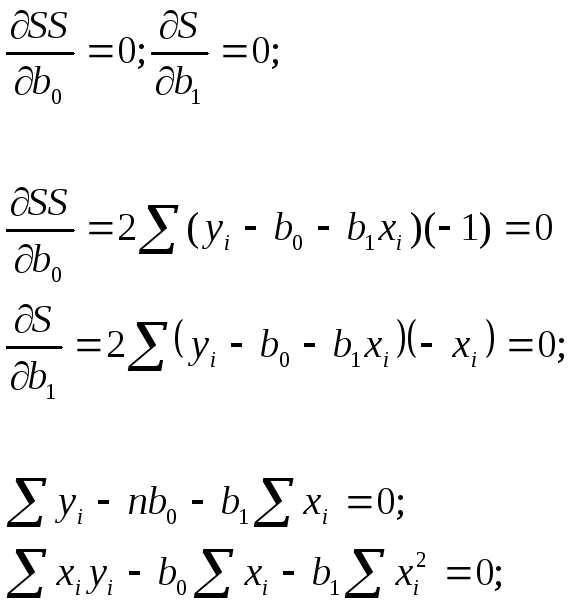
Полученную систему двух уравнений решим относительно оценок коэффициентов

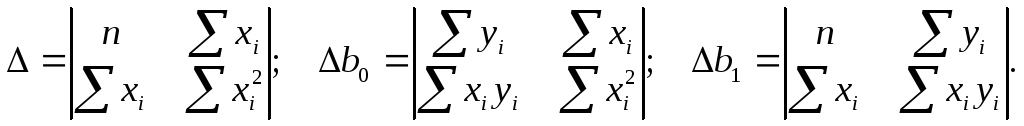
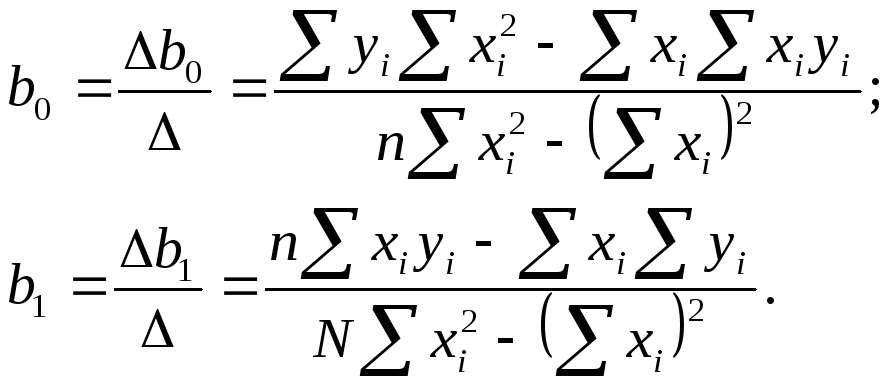
Алгоритм расчета коэффициентов представим в виде таблицы:

n/n	х	y	x2	y2	yx	x + y	(x + y)2
1	x1	y1
2	x2	y2
i	xi	yi

В таблице приведены дополнительные столбцы x + y, (x + y)². Эти данные нужны для проверки расчетов при ручном их выполнении.

Первая проверка:

Это выражение действительно для каждой строки, для суммарной строки.

Вторая проверка: для оценок коэффициентов и средних.

После проведения всех расчетов, подтверждается правильность данного выражения.

Аналогично производится вывод выражений для коэффициентов уравнения второго порядка и т.д.

Проведем анализ коэффициентов МНК

Рассмотрим выражение для оценки

Здесь в числителе сумма парных произведений xy, в знаменателе сумма квадратовx² в отклонениях от средних. Имеет аналогию с уравнением с динамическим звеном.

Проведем анализ выражения

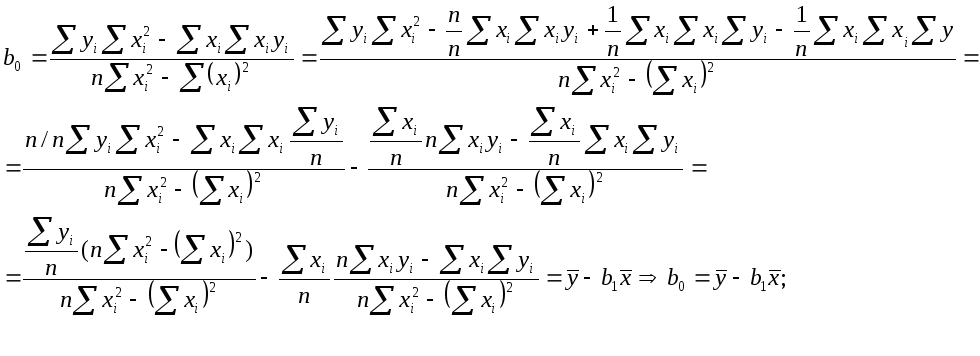
Рассмотрим два варианта записи уравнений регрессии