Уравнение винера-хопфа

Это уравнение свертки, в котором входной сигнал является , а выходной -.

,

где ,=0

Таким образом,

- влияние шума.

Корреляционный метод позволяет исключить или пропустить через фильтр влияние некоторых шумов.

Вывод уравнения винера-хопфа

Запишем уравнение через промежуток свертки:

Домножим уравнение на , получим:

Возьмем интеграл по , получим:

- характеристика звена

вынесем из-под знака внутреннего интеграла, получим:

Применение t-критерия

Чтобы оценить доверительный интервал, используют t-критерий, при заданном уровне значений и количестве экспериментов υ, где υ используют для того чтобы узнать на какой кривой необходимо работать.

В качестве могут быть случайные величины, например, коэффициенты корреляции и коэффициенты регрессии.

Например, имеется случайная величина. Оценка случайной величины может отличаться от истинной характеристики и от оценки, например, коэффициента регрессии при истинном нулевом значении, при этом сама величина может быть ненулевой.

Например, истинное значение отличается от оценки не более чем на величину , если наша оценка больше чем, то считается, что значение.

Оценка значимости величины

Величину можно найти, исходя из следующих критериев:

№	Наименование проверки	Тип критерия
1	Проверка значимости и построение доверительных интервалов для оценок ,	t-критерий (распределение Стьюдента)
2	Оценка дисперсий случайных величин ,,	- распределение
3	Оценка отношений дисперсий при анализе адекватности модели	F-критерий

t-критерий,- распределение,F-критерий – значения табличные и находятся по справочникам. Эти функции распределены, аппроксимированы математически и значения критериев получаются при использовании соответствующих команд.

Функции распределения зависят от количества экспериментов, и для учета этого фактора вводится понятие – число степеней свободы.С точки зрения математики, это избыточность информации над количеством уравнений связи, а, с точки зрения объекта управления, это количество независимых выходных переменных.

- Распределение

Проведем эксперимент. Рассмотрим множество реализаций случайного процесса и для каждого случайного процесса произведем выборку значений.

1	2	3
…	…	…

Введем нормализованные, то есть стандартные переменные:

Найдем квадраты этих переменных:

Рассчитаем сумму:

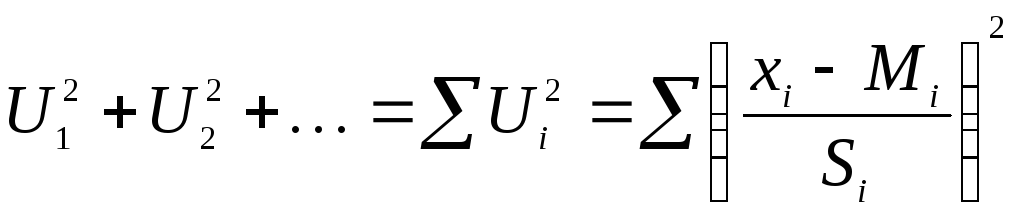
Полученную случайную величину, обозначим:

Это случайная величина, которая имеет все характеристики случайных величин, в том числе функцию распределения.

- распределение интересно тем, что такая величина получается при анализе дисперсии, а дисперсия это характеристика разброса случайных величин.

Если мы имеем дело с системой измерений, то эта характеристика будет являться точностью измерения. Если это система регулирования, то характеристика будет являться точностью регулирования.

Функция распределения зависит только от числа степеней свободы, то есть функция распределения является функцией от числа степеней свободы.