
- •Природа образования случайных процессов
- •Характеристики случайных процессов
- •Математическое ожидание
- •Функция распределения
- •Нормальный закон распределения
- •Закон больших чисел
- •Влияние параметров на вероятность
- •Характеристики скорости изменения случайных процессов во времени
- •Корреляционная функция
- •Белый шум, цветные сигналы
- •Спектральная плотность
- •Постановка задачи построения математической модели (идентификация)
- •Критерий теории мнк (метод наименьших квадратов)
- •Задачи нелинейного программирования
- •Основные виды зависимостей между переменными
- •Регрессионный анализ. Постановка задачи
- •Регрессионный анализ
- •Предпосылки регрессионного анализа
- •Вывод уравнений коэффициентов методом наименьших квадратов для дополнительного объекта
- •Метод наименьших квадратов в матричном виде
- •Построение нелинейной модели путем линеаризации
- •Методика получения нелинейного уравнения аппроксимируя экспериментальные данные
- •Метод нелинейного программирования
- •Уравнение винера-хопфа
- •Вывод уравнения винера-хопфа
- •Применение t-критерия
- •Оценка значимости величины
- •- Распределение
- •Количественные характеристики - распределения
- •Односторонний критерий
- •Показатели адекватности математической модели. Коэффициент множественной корреляции
- •F-критерий адекватности математической модели
- •Блок-схема построения математической модели
Метод наименьших квадратов в матричном виде
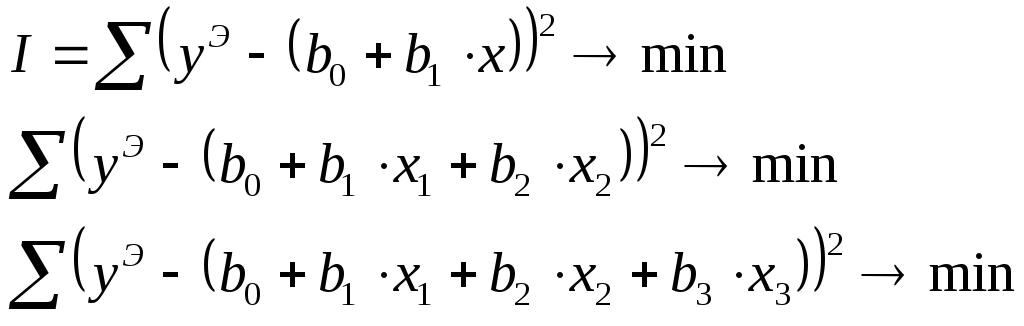
Были получены коэффициенты:
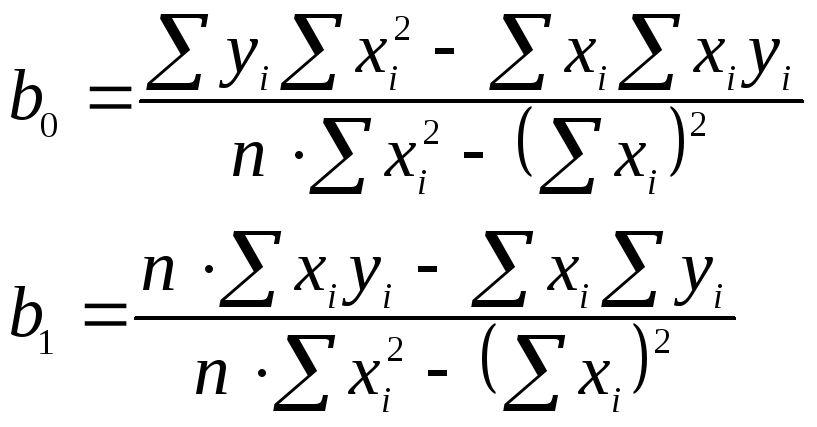
![]()
Для уравнения 1-го порядка экспериментальные данные будут иметь вид:
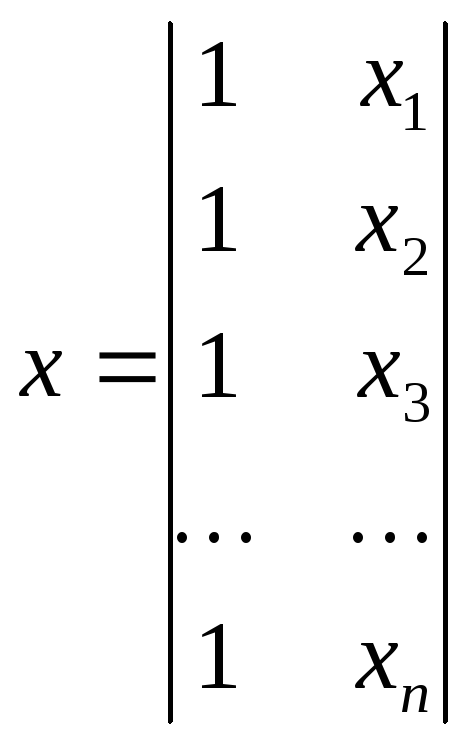
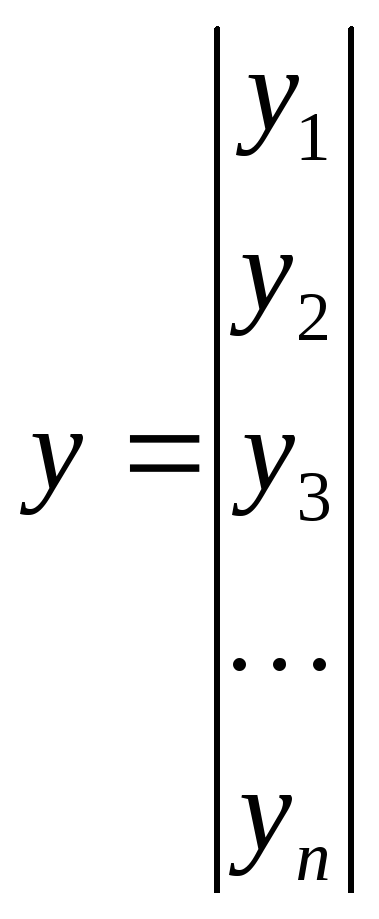
![]()
![]()
Найдем автокорреляционную матрицу
вектора
![]() :
:
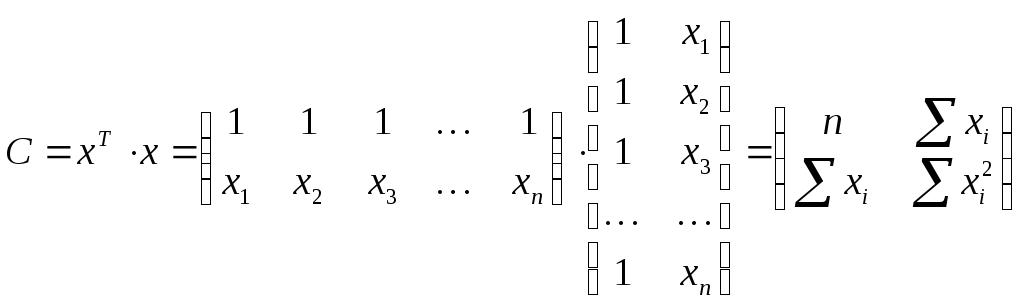
Умножим матрицу С на матрицу коэффициентовВ,то есть
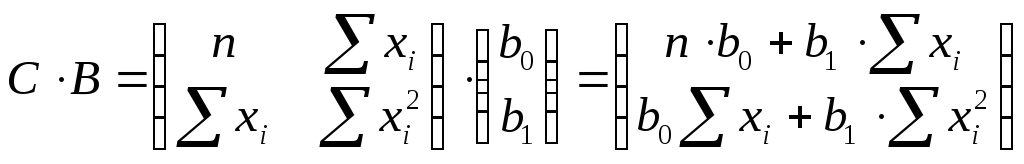
Находим взаимокорреляционную матрицу:
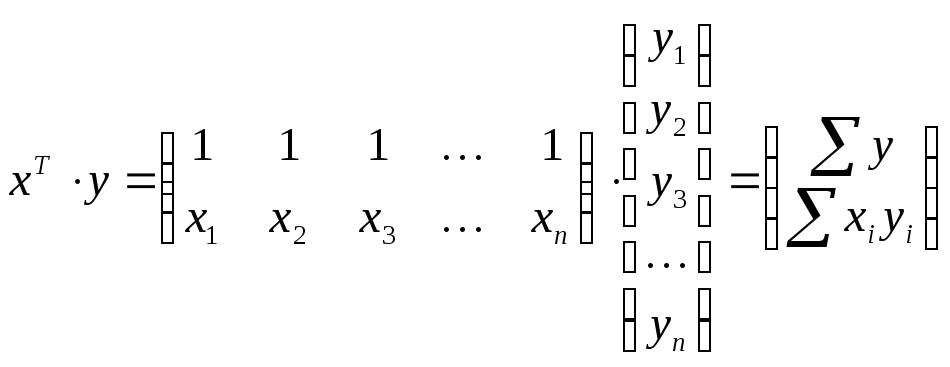
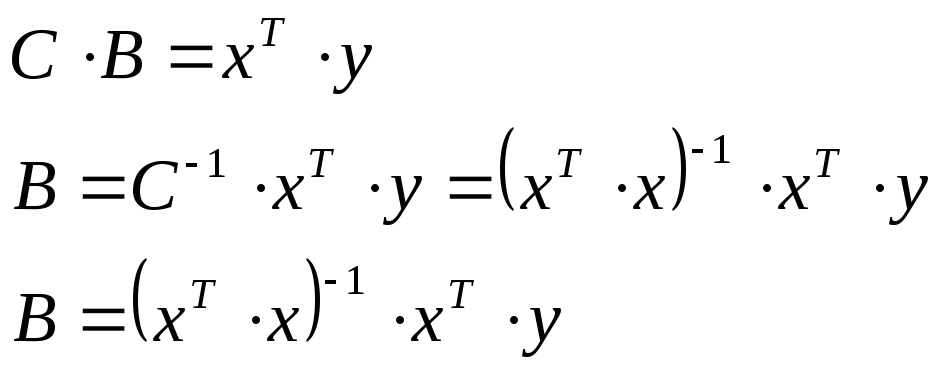
Построение нелинейной модели путем линеаризации
Нелинейное уравнение находится двумя способами:
Метод линеаризации
Использование метода нелинейного программирования
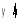
![]()
![]() -
экспериментальные значения
-
экспериментальные значения
Проведем логарифмирование обеих частей уравнения (1):
![]()
где
![]() ,
,![]() ,
,![]() ,
,![]()
Тогда уравнение (1) примет вид:
![]()
Получим линейно-регрессионное уравнение,
коэффициенты которого
![]() и
и![]() можно определить, но вместо экспериментальных
данных нужно использовать
можно определить, но вместо экспериментальных
данных нужно использовать![]() и
и![]() .
.
Находим
![]() и
и![]() .
.
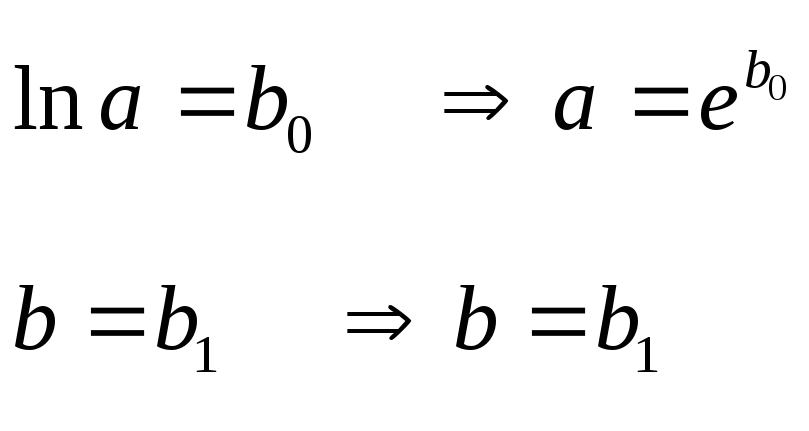
Получив оценки коэффициентов
![]() и
и![]() ,
находим коэффициенты регрессионного
уравнения.
,
находим коэффициенты регрессионного
уравнения.
Методика получения нелинейного уравнения аппроксимируя экспериментальные данные
Получить экспериментальные данные векторов
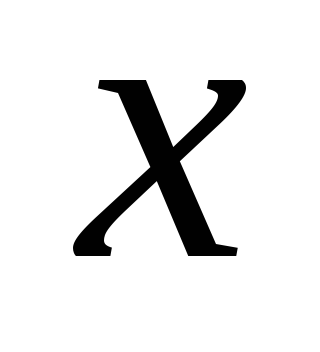 и
и .
.Построить график
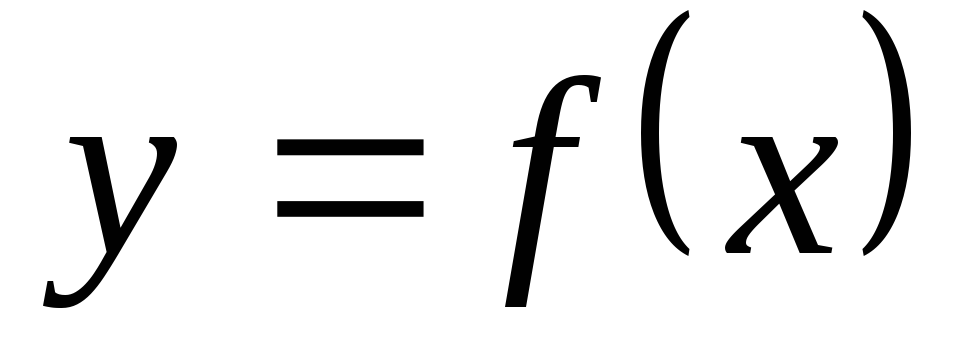 .
.Провести анализ графика и подобрать вид уравнения, воспользовавшись справочным материалом.
Подобрать закон преобразования переменных
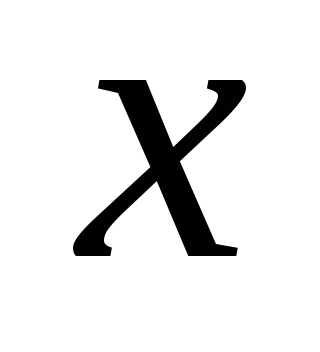 и
и в
в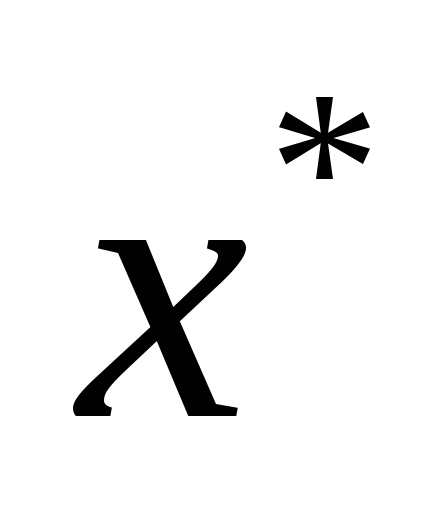 и
и ,
чтобы получить искомое уравнение.
,
чтобы получить искомое уравнение.Пересчитать значения
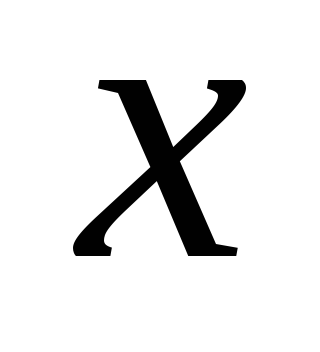 и
и в
в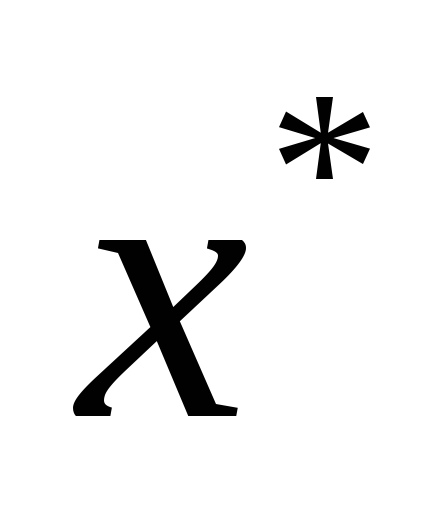 и
и .
.Найти коэффициенты
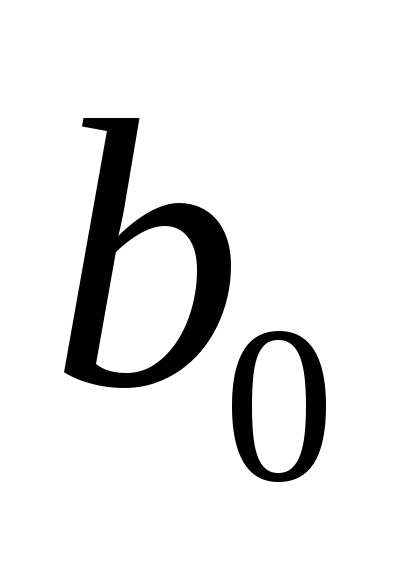 и
и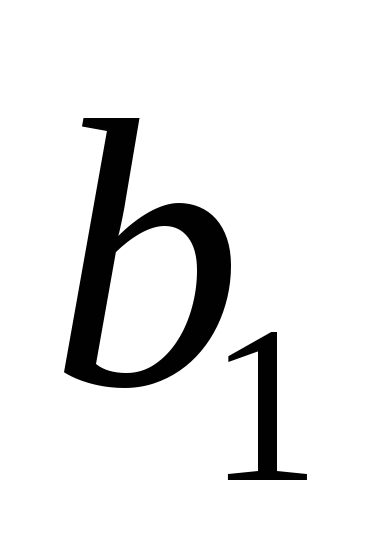 в уравнении
в уравнении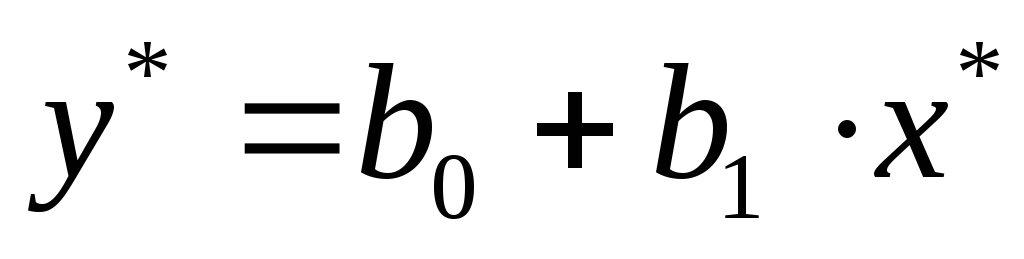
Построить график
![]() .
Найти зависимость, что эта функция
является прямой линией и рассчитать
значения
.
Найти зависимость, что эта функция
является прямой линией и рассчитать
значения![]() ,
правильно описывающие пересчитанные
значения экспериментальных данных.
,
правильно описывающие пересчитанные
значения экспериментальных данных.
По коэффициентам
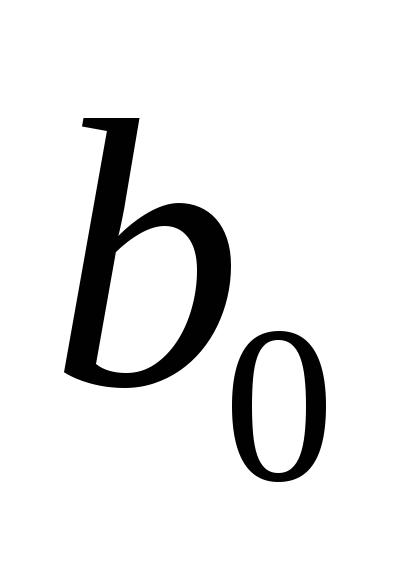 и
и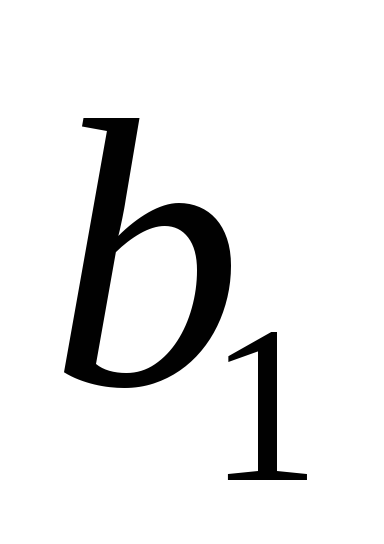 ,
найти коэффициенты
,
найти коэффициенты и
и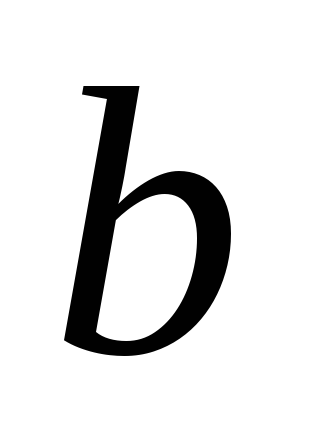 исходного нелинейного уравнения.
Рассчитать значение
исходного нелинейного уравнения.
Рассчитать значение ,
построить график на исходном графике.
Расчетные значения должны лежать по
середине корреляционного поля.
,
построить график на исходном графике.
Расчетные значения должны лежать по
середине корреляционного поля.Найти количественную оценку точности аппроксимации:
а) Остаточную дисперсию
![]()
б) Абсолютную ошибку аппроксимации
![]()
ПРИМЕЧАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ № 4
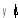
![]()
![]()
![]() ,
где
,
где![]()
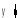
![]()
![]()
![]() ,
где
,
где![]()
|
№ |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения коэффициентов
![]() и
и![]() используетсяExcel. Выделим
на графике
используетсяExcel. Выделим
на графике![]() ,
выбираем экспериментальные точки,
нажимаем правую кнопку мыши, выбираем
линию тренда, линейная зависимость,
выдать уравнение, выдать
,
выбираем экспериментальные точки,
нажимаем правую кнопку мыши, выбираем
линию тренда, линейная зависимость,
выдать уравнение, выдать![]() .
.
Выдает уравнение
![]() ,
график зависимости
,
график зависимости![]() от
от![]() .
.
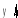
![]() ,
,
где
![]() ,
,![]() ,
,![]()
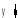
![]()
![]() ,
,
где
![]() ,
,![]() ,
,![]() ,
,![]()
Метод нелинейного программирования
Применяется при наличии статических характеристик колебаний (шум) на экспериментальной переходной характеристике. Рассмотрим метод с использованием разностных уравнений. Данный метод позволяет построить модель и для ступенчатого входного сигнала, а также для любого изменения входного сигнала.
Рассмотрим апериодическое звено 1-го порядка
![]()
![]()
Решение данного уравнения при ступенчатом
входном сигнале
![]() определяется суммой следующих выражений.
определяется суммой следующих выражений.
![]()
![]() (1)
(1)
![]() -
свободное отношение
-
свободное отношение
![]() -
вынужденное отношение
-
вынужденное отношение
В уравнении (1) учтены начальные значения
![]() и влияние входной переменной
и влияние входной переменной![]() .
.
Используя данное решение для нахождения
выходного сигнала при любом его законе
изменения. Постоянное значение
![]() также входит в данное множество решений.
также входит в данное множество решений.
Произведем дискретизацию во времени входного сигнала, то есть будем брать момент
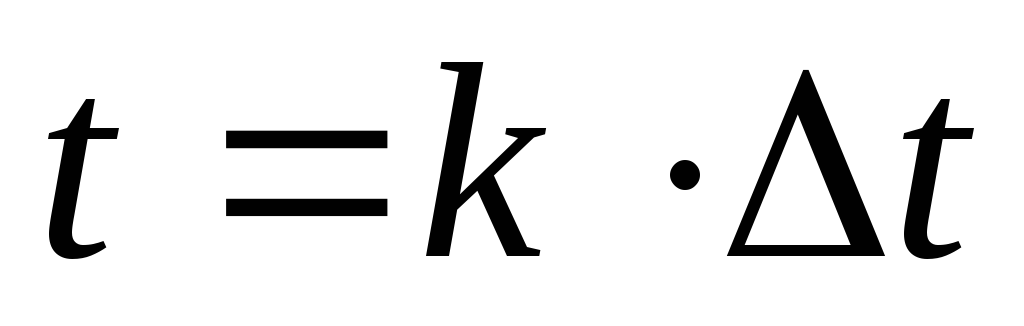 ,
где
,
где -
период дискретизации.
-
период дискретизации.
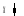
![]()
![]()
Для нахождения
![]() необходимо знать следующее:
необходимо знать следующее:
Дифференциальное уравнение
Параметрическое дифференциальное уравнение
Начальные условия:
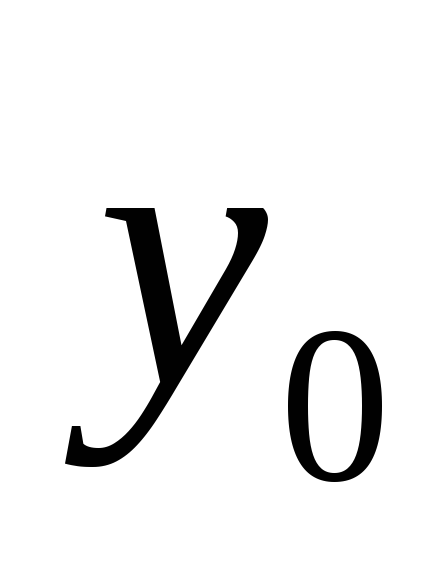
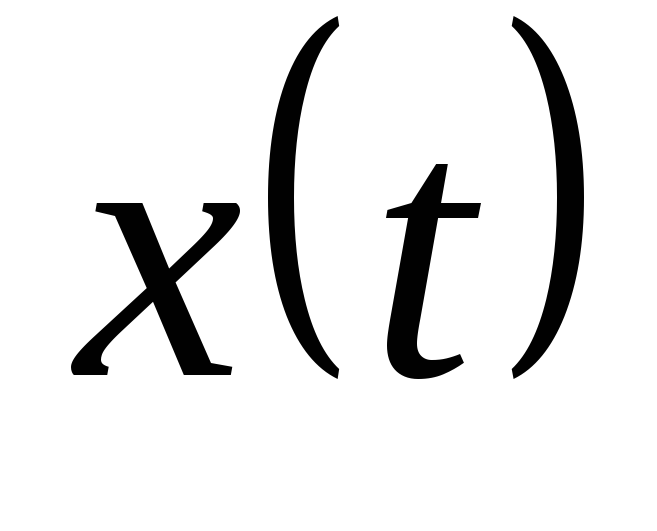
Рассмотрим решение входного сигнала ступеньки на 1-ом периоде дискретизации.
Запишем начальные условия.
![]()
![]()
![]()
![]()
![]()
…
![]()
![]()
![]()
![]()
![]() - разложение уравнения для апериодического
звена 1-го порядка
- разложение уравнения для апериодического
звена 1-го порядка
Данное уравнение позволяет изменить выходной сигнала для любого закона изменения входного сигнала.
Звено 2-го порядка, то есть апериодическое звено.
Найдем корни этого звена.
![]()
![]()
![]()

Реально-интегрирующее звено.
![]()

![]()
![]()
![]()
Запишем 3 системы разных уравнений, которые позволяют описать 3 наиболее распространенные модели объектов управления.
Рассмотрим задачу построения модели по экспериментальным переходным характеристикам:
Проведем планирование эксперимента.
Проверим характеристики сигналов при ступенчатом изменении входных сигналов и получим графики переходных процессов.
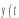
![]()
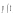
![]()
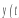
![]()
По виду кривых мы можем выбрать вид уравнений, то есть структуру математической модели. Иногда четкого разделения сделать нельзя, поэтому строится несколько моделей и показывается адекватность этих моделей. На основе адекватности моделей выбирают более точную. На данном этапе мы провели структурную идентификацию и выбрали вид уравнения. Следующим этапом параметрической идентификации, то есть получения параметров и коэффициентов модели, для нахождения параметров применим метод нелинейного программирования.
Применение численного метода оптимизации.
Постановка задачи
Возьмем 1-ое звено с передаточной функцией:
![]()
Запишем
![]()
![]() ,
,![]()
![]() (1)
(1)
![]() (2) при
(2) при![]() (3)
(3)
Ограничение типа неравенства формирует
решение из возможных физически допустимых
решений. Задачей является нахождение
таких значений
![]() и
и![]() ,
чтобы при выполнении уравнений (2) и (3)
критерий имел минимальное возмущающее
значение. Такие задачи решаются численными
методами оптимизации.
,
чтобы при выполнении уравнений (2) и (3)
критерий имел минимальное возмущающее
значение. Такие задачи решаются численными
методами оптимизации.
