Регрессионный анализ. Постановка задачи

Проведем построение математической модели линейного по параметрам объекта. Объект описывается уравнениями:

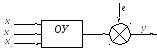
y = β₀ + β₁x₁ + β₂x₂ + … +β_nx_n.

Математическая модель находится как:

ŷ= b₀ + b₁x₁ + b₂x₂ + … + b_nx_n

x₁, x₂…x_n – вектор конкретных параметров.

B = b₀, b₁, … b_n– вектор параметров модели.

Регрессионный анализ

Регрессионный анализ включает в себя:

1. Метод наименьших квадратов, используемый для оценки параметра вектора коэффициентов.

2. Дисперсионный анализ используется для оценки адекватности модели и для оценки значимости коэффициентов.

Предпосылки регрессионного анализа

1. Количество экспериментальных данных должно иметь 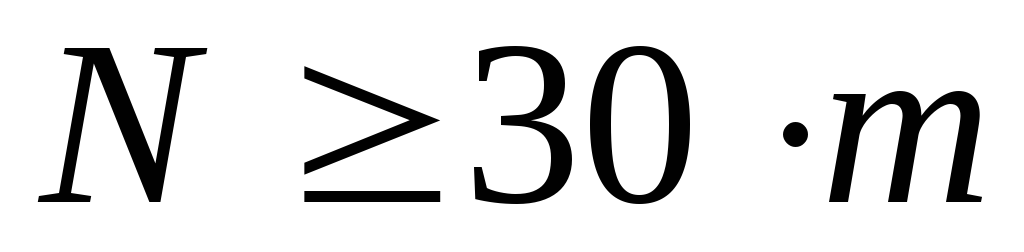, гдеN– количество экспериментов,m– количество входных факторов.

2. Выходная переменная имеет нормальный закон распределения.

3. Выходная переменная стационарна по дисперсии, то есть дисперсия выходного параметра в процессе эксперимента не изменяется.

4. Входные переменные являются детерминированными, то есть измеряются с малыми ошибками.

5. Входные переменные х₁, х₂, … х_nстохастически не связаны между собой, то есть коэффициент парной корреляции равен нулю.

6. Следующие друг за другом значения выходной переменной также не коррелированны, то есть период дискретизации больше времени затухания корреляционной функции.

Примечание.В практике часто не выполняются некоторые предпосылки регрессионного анализа. При использовании этого метода необходимо учитывать, что полученная модель может не точно описывать процесс и необходимо проверить модель, произведя дополнительные эксперименты.

Вывод уравнений коэффициентов методом наименьших квадратов для дополнительного объекта

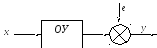
Для данного объекта выполняются предпосылки регрессионного анализа.

Допустим, имеется таблица экспериментов N≥30.

N	xi	yi
1	x1	y1
2	x2	y2
3	x3	y3

Выходная переменная yимеет нормальный закон распределения:

Y = N(a, S, R);

S² = const.

Ошибка в измерении входной переменной равна нулю, тогда корреляционная функция будет иметь вид

R_{xi yi} (τ) → 0

Построим график зависимостиуотх– корреляционное поле

х

х₁

х₂

Определим зависимость у(х) по двум экспериментальным точкам, которые с математической точки зрения, количество точек являющиеся достаточным для определения двух коэффициентовb₀,b₁. Задачей является использовать все экспериментальные данные и найти единственную зависимость, которая считается наилучшей.

Выберем такую линию, которая является средней линией корреляционного поля. Математически она может быть выражена как линия, которая имеет минимальную сумму квадратических отклонений от всех экспериментальных точек.

Данное выражение является критерием уравнения модели:

Это выражение позволяет найти уравнения для определения коэффициентов b₀,b₁ при условии, чтоSS → min.

Условием экстремума функции является равенство нулю производной данной функции по исследуемому параметру, то есть по параметрам b₀, b₁.

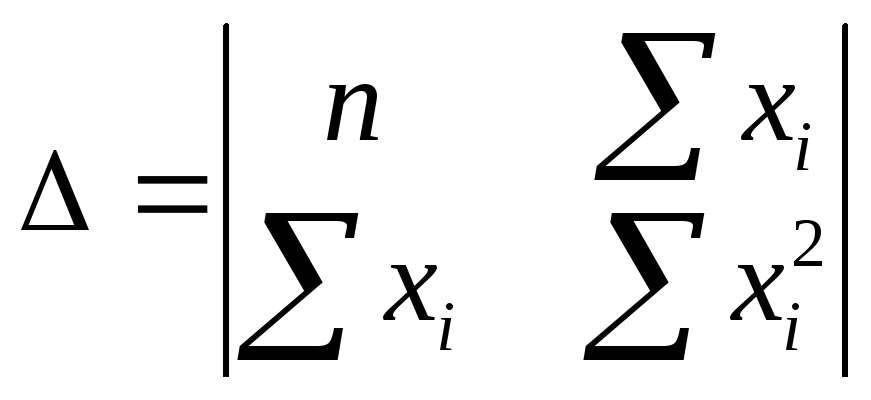
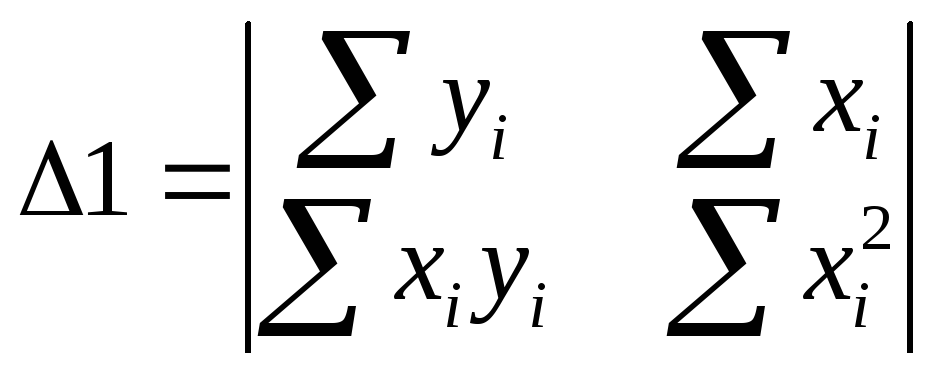
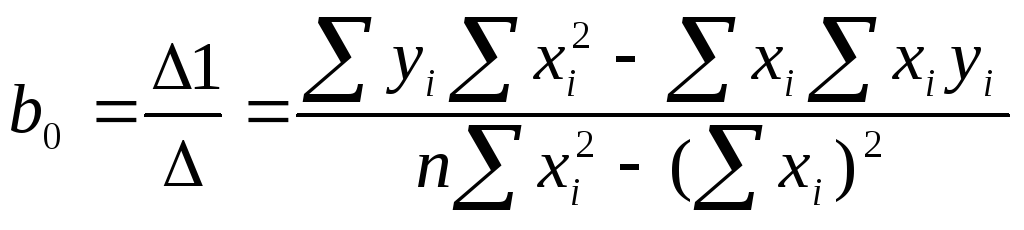
ПРИМЕЧАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ № 3

Построение линейной одномерной модели.

№
1
2

Если ошибка будет обнаружена в коэффициенте , то линия тренда пройдет либо выше, либо ниже корреляционного поля.

Несовпадение графиков расчетной линии с корреляционным полем означает наличие ошибки в расчете, таким образом, необходимо провести проверку в расчете.

Оценка ошибки расчетного значения :

Ошибка - нормальная распределенная случайная величина с нулевым средним значением и дисперсией. Ошибка модели на каждом шаге определяется разностью количественной оценки, которая является дисперсией в данном случае остаточной

- число степеней свободы, уменьшается отдля расчета среднего отдопо мере использования экспериментальных данных, в данном случае, где- количество коэффициентов уравнения без учета.

Примечание. Диапазон колебаний случайной величины характеризуется связанными между собой двумя величинами:

1. Дисперсия, которая легко рассчитывается по экспериментальным данным;

2. Коридор ошибки на временном графике. Зависит от доверительной вероятности, для

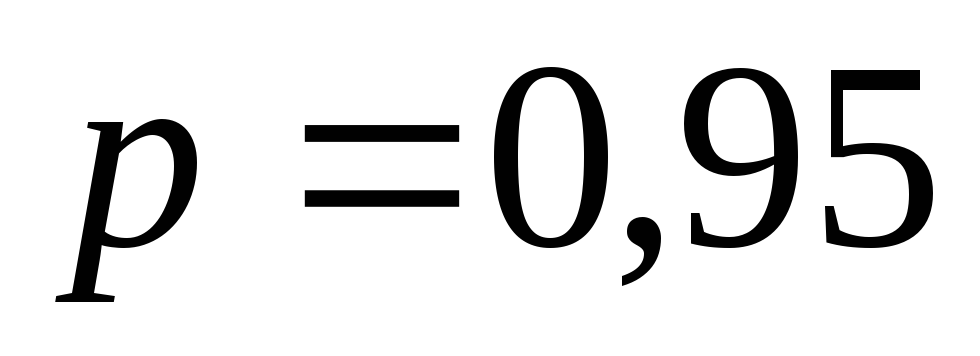
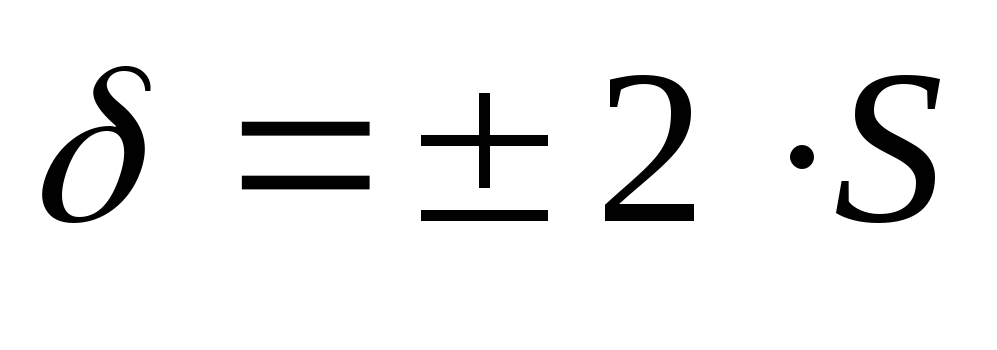
- абсолютная остаточная ошибка.