Функция распределения

Пусть случайная величина принимает значения в диапазоне от 50 до 100. Разобьем диапазон на коридоры и подсчитаем количество точек в каждом диапазоне.

Нормальный закон распределения

n_i(x)– частота вi-том диапазоне

где - относительная частотность

– функция распределения, которая является теоретической величиной . Она показывает вероятность принятия случайной величиной конкретного значенияx_i, а для непрерывной случайной величины вероятность нахождения случайной величины в коридоре, определяемом какx + Δx.Полученный экспериментальный график называетсягистограммой.

Гистограмма– это экспериментальная оценка функции распределения. В практике имеет место большое количество функций распределения. Мы будем рассматривать нормальный закон распределения, закон распределения Стьюдента.

Закон больших чисел

Если случайная величина зависит от большого количества других случайных величин с любым законом распределения, и вклад которых примерно одинаков, то есть, нет доминирующего влияния одного или нескольких факторов, то случайная величина имеет нормальный закон распределения.

Влияние параметров на вероятность

Введем параметры надежности оценок, а именно, доверительный интервал и доверительную вероятность.

а – среднее

Рассмотрим детерминированную величину y=f(x),значениеуможет быть точно спрогнозировано, то есть, определено для любого значениях, то есть для каждого значенияхимеется точное значениеу. Предположим, чтоу=5, вероятность того, чтоу=5равна единице, но можно характеризовать у двумя числами, то естьу=5 с вероятностьюр=1.

Случайную величину нельзя спрогнозировать точно, но можно указать диапазон, в котором случайная величина может находиться. Причем, чем шире указанный диапазон, тем больше вероятность попадания случайной величины в данный диапазон.

Случайная величина характеризуется двумя параметрами:

1. Заданный коридор – это доверительный интервал

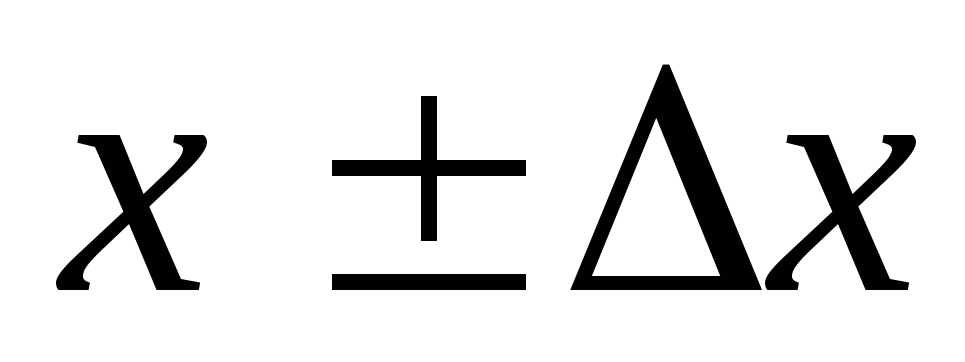
2. Вероятность попадания в данный интервал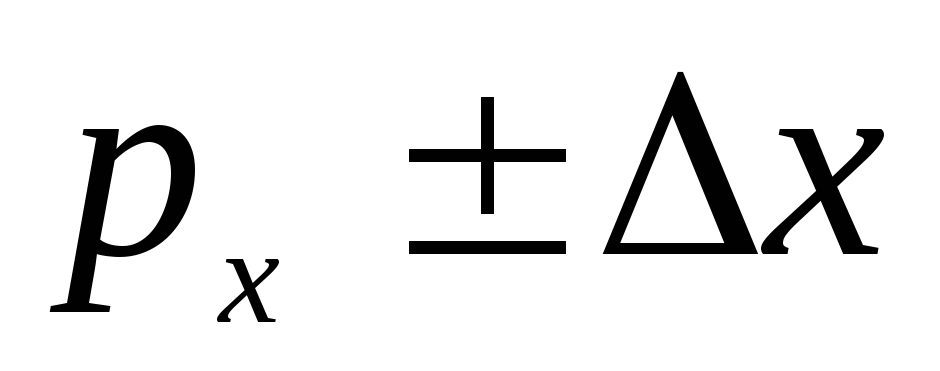- доверительная вероятность.

a± 1σ→ 68%

a± 2σ→ 95%

a± 3σ→ 99.7%

С доверительной вероятностью р = 2 хпринимает значения:

Запишем доверительный интервал для данной случайной величины. Для решения необходима доверительная вероятность, запишем решение для трех случаев: Если

μ = 1 а = 0,68 р₁= 0,68 μ = ±2

μ = 2 а = 0,95 р₂= 0,95 μ = ±4

μ = 3 а = 0,997 р₁= 0,997 μ = ±6

В практике для решения этих задач используют доверительную вероятность р = 0,95; в медицинер = 0,997. Если не оговаривается доверительная вероятность, то считается, что случайная величина находится в коридорепри этом 0,3% данных могут вылетать из коридора.

Характеристики скорости изменения случайных процессов во времени

Любой случайной процесс можно разбить на гармоники.

Представим процесс в виде суммы четырех гармоник:

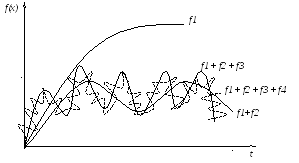
Данные сигналы имеют различные спектральные составляющие.