1. Случайные сигналы

Случайные сигналы в системах управления изменяются во времени. Поэтому для их описания используется теория случайных процессов. Случайные процессы, вследствие действия неконтролируемых возмущений, нельзя задать явной математической функцией и спрогнозировать конкретное значение случайной величины. Но изучив закономерности данного случайногопроцесса и влияющих на него величин, можно прогнозировать уровень случайных величин, коридор их изменения и управлять этими хапрактеристиками.

К ратко рассмотрим основные характеристики случайных процессов. На рисунке приведены графики 2-х случаных процессов, отличающихся как средними значениями, вокруг которых происходят колебания случайных процессов , так и диапазонами их колебаний .

Среднее определяется по выражению и является оценкой математического ожидания, которое является характеристикой уровня случайного процесса.

Диапазон изменения случайной величины характеризуется оценкой дисперсии случайной величины. Оценка дисперсии определяется по выражению

Здесь и выше - объем выборки для определения среднего и дисперсии

- число степеней свободы выборки, обеспечивающее получение несмещенных оценок характеристик.

Теоретические значения параметров некоторых случайных процессов можно определить теоретически. Но в практике чаще используют их оценки, которые определяют по экспериментальных данным. Оценки, естественно, отличаются от теоретических значений матожидания, дисперсии и других характеристик случаных величин и в каждой выборке имеют свое значение, т.е. сами являются случайными величинами. Истинные значения матожидания, дисперсия и другие характеристики являются параметрами всей генеральной совокупности. В принципе, их можно получить как оценки, если в качестве выборки использовать всю генеральную совокупность случаного процесса, но это практически невозможно.

Данные случайные процессы еще могут различаться законом распределения значений внутри коридора изменения. В одних процессах значения больше «толпятся» около среднего значения у других больше значений ближе к одному или двум краям коридора и др. Зависимоть вероятности принятия определенных значений случайной величины (или коридора значений для непрерывной случайной величины) от этих значений называется функцией распределения.

При моделировании систем управления часто используемые случайные процессы со следующими функциями распределения.

1. Равномерное распределение. Графики дифференциальной и интегральной плотностей вероятности равномерной случайной величины приведены на рисунке . Плотность распределения вероятности в диапзоне возможных значений переменной есть величина постоянная .

Учитывая, что вероятность нахождения случайной величины в коридоре равна 1 определим значение вероятности с

Тогда дифференциальная функция имеет вид

Получим количественных характеристики равномерного распределения

Математическое ожидание: ;

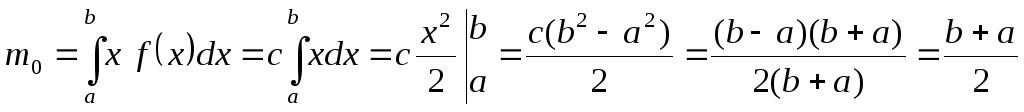На основании свойств дисперсия может быть определена по выражению .

Определим матожидание квадрата переменной

Тогда

Случайные величины с равномерным распределением используются при генерации случайных величин с заданными характеристиками.

2. Нормальное распределение (распределение Гаусса). График нормального закона распределения приведен на рисунке . Дифференциалный закон распределения описывается выражением

Место положения центра кривой определяется математическим ожиданием a, а ширина распределения - дисперсией случайной величины .

Нормальное распределение имеет наиболее широкое распространение, т.к. обычно случайные величины определяются влиянием большого количества факторов, а в центральной предельной теореме Ляпунова показано, что если случайная величина является суммой большого числа взаимно независимых случайных величин (с любым законом распределения), влияние каждой из которых на сумму мало, то данная величина имеет нормальное распределение.

Для практического применения важно связать дисперсию нормальной случайной величины с коридором ее изменения во времени. При этом назначают короидор (квантиль) и надежность (вероятность) нахождения случайной величины в данном коридоре, допуская, что какае-то количество значений имеет право выходить за заданный коридор. Для нормальной случайной величины в коридоре находится 68% значений, соответственно, в коридорах и находятся 95% и 99.6% значений случайной величины (см рисунок ).

Отметим, что приведенные значения строго справедливы для нормального распределения, но при больших объемах выборки они справедливы и для некоторых других законов распределения.

На рисунке прведены графики трех случайных процессов x₁(t), x₂(t), x₃(t) не отличающихся своими средними значениями, дисперсиями и законами распределения. Но они отличаются скоростью изменения случайных величин во времени или, говорят, они имеют различные спектральные составляющие. Эти свойства случайных проессов надо учитывать при анализе систем управления, тк сигналы с различными частотами отрабатываются элементами ситемы поразному (согласно частотным характеристикам).

Для учета этих свойств введем две взаимосвязанные характеристики.

Корреляционная функция

Спектральная плотность

Корреляционная функция – это зависимость коэффициента корреляции r_xx, определенного для различных сдвигов  от . Оценка корреляционной функции для различных сдвигов определяется выражениями:

1. =0;

2. =1;

3. =2;

Теперь построим графики R_xx() – это и есть корреляционная функция, в данном случае автокорреляционная, т.к. анализируется связь x(t) с x(t+τ).

Основные свойства корреляционной функции.

1. R₀ – есть дисперсия сигнала (ненормированной корреляционной функции)

2. Время затухания корреляционной функции тем больше, чем, более плавно изменяется x, t₃>t₂>t₁, что и требовалось выявить в графиках.

Спектральная плотность – прямое преобразование Фурье от корреляционной функции .

Рассмотрим физический смысл спектральной плотности. Рассмотрим случайный сигнал на рисунке : его можно представить в виде суммы 4-х компонент

- среднее значение

- низкочастотный

- среднечастотный

- высокочастотный

Дисперсия х равна сумме дисперсий компонент , , .

Построим график зависимости дисперсии х от частоты. Мы получили распределения дисперсии х по частотам. Это и есть спектральная плотность. Площадь под кривой S() есть дисперсия . Дисперсия по определению - среднее значение квадрата отклонения случайной величины от среднего значения. Рассмотрим мощность, выделяющуюся в электрической цепи на сопротивлении с R = 1Ом

Видим, что мощность электрического тока пропорциональна не величине, а квадрату электрической величины - тока или напряжения. Следовательно, дисперсия характеризует мощность переменной составляющей случайного процесса. Тогда физический смысл спектральной плотности – это разложение мощности сигнала по частям. Спектральная плотность S() показывает, какие гармоники или частотные составляющие есть в сигнале и какая относительная мощность этих гармоник.

С другой стороны спектральная плотность - разложение дисперсии определяет разложение ошибки системы по частотам и характеризует отработку системой возмущений на различных частотах.

Пример использования спектральной плотности при анализе системы.

Пусть задана математическая модель динамической системы, например, в виде передаточной функции и модель входного сигнала в виде спектральной плотности . Необходимо определить дисперсию сигнала на выходе динамической системы.

Алгоритм расчета следующий.