лекции / Идентификация объектов управления - УП - Семёнов-Артамонов-Брюхачев - 2003 - 215

Тогда дискретный аналог модели исполнительного механизма будет выглядеть x1(k +1) = e−h x1(k) + (1−e−h )u(k)

x2 (k +1) = (1−e−h )x1(k) + x2 (k) + (h −1+ e−h )u(k) .

Этот пример в MATLAB для h=0,1 запишется так

A=[-1 0;1 0]; B=[1;0]; C=[0 1]; D=0;

sn=ss(A,B,C,D) % Модель непрерывной системы

h=.1; % Период дискретизации sd=c2d(sn,h) % Модель дискретной системы

Полученные непрерывная и дискретная модель будут выглядеть:

Непрерывная модель

u1

y1 0 Continuous-time model.

Дискретная модель a =

u1

y1 0 Sampling time: 0.1 Discrete-time model.

2.5. Математические модели на базе матричных операторов.

При исследовании нестационарных и нелинейных систем использование линейных моделей, рассмотренных в п. 2.1- 2.4 становится громоздким и неэффективным, поэтому возникла идея создания методов использующих аппарат матричных операторов и спектральную форму описания процессов [4, 5, 49, 60]. Аппарат матричных операторов базируется на использовании теории ортогональных функций использующей в качестве базиса не только тригонометрические, но и другие виды ортогональных функций образующих новые базисы. В качестве таких функций используют полиномы Лежандра, Чебышева, Лагерра, функции Уолша и др.

Метод матричных операторов и спектральные методы предполагают разложение сигналов и временных динамических характеристик системы по ортогональным базисам.

Пусть Φ[ϕ1(t),ϕ2 (t),...ϕn (t)]T одностолбцовая матрица элементов

ортонормированного базиса порождающее в общем случае некоторое банахово пространство функций. Тогда произвольный сигнал системы x(t) заданный на

называют матричным оператором или спектральной характеристикой системы относительно ортонормируемого базиса Ф×Ф.

Вводя, по аналогии с типовыми динамическими звеньями линейных систем, типовые матричные операторы интегрирования, дифференцирования и умножения можно формировать из этих операторов матричные структурные схемы системы в выбранном базисе.

Причем для таких структурных справедливы те же правила преобразования, что и для линейных систем.

Матричный оператор последовательного соединения элементов равен произведению матричных операторов отдельных элементов

Сx Сy

Следует обратить внимание на то, что матричные операторы перемножаются от выхода ко входу.

Матричный оператор параллельного соединения элементов равен сумме матричных операторов отдельных элементов

произведением матричного оператора прямой цепи на матричный оператор

в базисе функций Уолша для входного сигнала x(t) = t заданного на интервале

времени [0, 1]. Поскольку функции Уолша принимают значения +1 и –1, то их

дискретным аналогом будут являться строки матрицы Адамара Φ(ti ) = H ,

элементы которой определяют значение функций на множестве

равноудаленных точек.

Построив матрицу Адамара, коэффициенты разложения функции x(t) можно вычислить по формуле

y=H*Cy % Вычисление интеграла от входного сигнала stairs(t,y) % Построение приближения выходного сигнала

hold on

plot(t,x.^2/2),grid % Построение выходного сигнала

hold off

Результаты расчетов

Матрица Адамара

H =

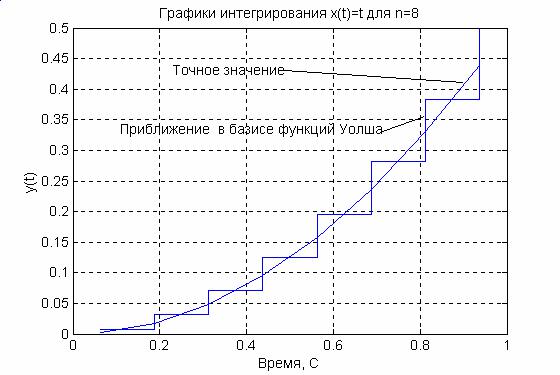
Значения выходного сигнала

y=[0,0078 0,0313 0,0703 0,1250 0,1953 0,2813 0,3828 0,5000]

Рис.2.13.

2.6. Математические модели нелинейных систем

на базе функциональных рядов Вольтерра – Винера

Данные модели являются дальнейшим развитием метода матричных

операторов и применяются для исследования нелинейных систем. В отличии от линейных для нелинейных систем нарушается принцип суперпозиции и

постоянство масштаба переменных. Вследствие этого становится неприменимым математический аппарат теории линейных систем, а в

нелинейных системах возникают многие явления, не имеющие места в линейном случае и связанные, например, с появлением комбинационных гармоник и расширением спектра выходного сигнала, возникновении автоколебаний и нелинейного резонанса.