лекции / УП_ИДС Игнатьевичь

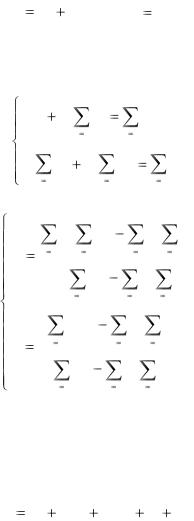
Функция регрессии определяется в виде соответствующего математического уравнения того или иного типа.

С помощью функции регрессии можно установить значение зависимой величины внутри интервала, заданные значения независимой переменной или же оценить в течении процесса внезапного интервала.

Внедрение в практику ЭВМ и разработка стандартных программ по регрессионному анализу существенно ускоряет и облегчает обработку больших массивов статических данных и дает возможность построения многократных моделей.

Под этой зависимостью понимают одностороннюю стохастическую связь.

наименьших квадратов по уравнению:

Помимо простой линейной регрессии может использоваться множественно линейная регрессия вида:

Расчет коэффициентов множественной регрессии осуществляются по регрессии, изложенной в специальной литературе.

Лекция № 14.

Нелинейная регрессия.

Под нелинейной регрессией понимают более сложную одностороннюю стохастическую зависимость, представимую в виде полиноминальной модели вида:

Могут применяться также степенные, показательные, логарифмические, тригонометрические, а также полиномы Чебышева и т. д.

Обычно подбор конкретной функции осуществляется на базе той науки в рамках которой изучается данный процесс.

Принято различать два класса уравнений нелинейной регрессии:

Первый класс – охватывает регрессии нелинейные относительно входного параметра х, но линейные относительно коэффициентов bi . Для таких регрессий

применим метод наименьших квадратов.

Второй класс – охватывает регрессии, которые являются нелинейными также относительно коэффициентов bi , что требует для применения итерационных

методов.

Достаточно часто в различных технических исследованиях исследуется параболическая регрессия к-го порядка.

Для случая к=2 такая регрессия имеет вид:

В этом случае для нахождения коэффициентов составляется система трех уравнений:

Необходимо иметь в виду, что после вычисления коэффициента bi всегда

должна осуществляться проверка их значимости по соответствующей методике и незначимые коэффициенты обнуляются.

Использование временных рядов в задачах идентификации.

При исследовании динамики процессов в технике, а также в экономике, биологии и в других науках, важную роль играют вопросы изучения характерных признаков последовательности возникающих значений.

По результатам наблюдений строятся хронологические (временные) ряды получаемых значений.

Для таких рядов разработаны специальные методы статистической обработки, которые называются авторегрессионными, поскольку значения членов временного ряда взаимосвязаны.

Идентификация моделей таких временных рядов производится итерационными методами, причем модели этих рядов бывают трех видов:

1.Авторерессионные модели

2.Модели авторегрессии со скользящим значением.

3.Авторегрессионые с проинтегрированным средним значением.

На основании соответствующих методик по указанным моделям может получена с достаточно высокой степенью точности прогнозирования развитие процесса.

Характерной особенностью авторегрессионных моделей временных рядов является то, что чем выше порядок модели, тем больше число членов временного ряда необходимо учитывать при прогнозировании и тем более сложной является их математическая зависимость.

Методы идентификации моделей временных рядов в последнее время интенсивно развивается, находит широкое применение в связи с интенсивным использованием ЭВМ.

Интерполяция с помощью сплайн – функции.

Данная интерполяция наиболее эффективна для построения гладких кривых, проходящих через заданные точки, полученные например, экспериментально.

Если имеется некоторое число n – точек, то при сплайне интерполяции через каждые две соседние точки проводят поленом третей степени.

Понятно, что по этим двум точкам нельзя однозначно определить коэффициенты этого полинома, поскольку две точки определяют только полином

Для выполнения этих условий значение первой и второй производных для соседних полиномов в их общей точке (xi , yi ) , т.е. должны выполняться:

Pi ' 1 (xi ) Pi ' (xi )

Pi '' 1 (xi ) Pi '' (xi )

Таким образом, для внутренних полиномов сформулировано четыре условия, которые достаточны для их построения.

Обе концевые точки исходного массива имеют только по одной соседней, поэтому для построения концевых полиномов требуются дополнительные условия.

Если принять, что точки, лежащие в не рассматриваемом интервале, можно аппроксимировать, то последнее условие можно записать в виде:

P1'' (x1 ) 0

Pn'' 1 (xn ) 0

На основании решения полученной системы, выполненной по определенной методике, можно полностью определить сплайн полиномы Pi .

А тогда для любого значения x можно рассчитать интерполяционное значение

x .

В настоящее время для реализации сплайн интерполяции существуют стандартные программы для ЭВМ.

Данный метод очень удобен с точки зрения представления гладких зависимостей, при условии, что наш изначально известно, что процесс является непрерывным и не имеет точек разрыва.

Регрессионная зависимость на основе сплайн используется для сглаживания экспериментальных данных и их более наглядного представления, причем степень сглаживания может задаваться самим исследователем.

При такой интерполяции сплайн функции проходят через все экспериментальные точки, причем эти точки совпадают с точками перегиба сплайн функции.

Если уменьшить число точек перегиба, то сплайн функция не будет точно проходить через экспериментальные точки.

Поэтому дополнительные условия для построения такой сплайн функции заключается в том, чтобы сумма квадратов отклонений заданных точек от аппроксимирующих функций была минимальна, т.е. точки должны располагаться на одинаковом расстоянии от соответствующих кривых.

Чем меньше число точек перегиба, тем более гладкой получится кривая, тем дальше будет проходить в стороне от заданных точек.

Идентификация моделей процессов методом планирования экспериментов

(Изучено нами самостоятельно).

Техническая диагностика систем.

Важной и актуальной проблемой является проблема обеспечения качества и надежности функционирования сложных технических систем.

Распознавание технического состояния объекта на важных этапах его жизненного цикла представляет собой задачу технического диагностирования.

Техническая диагностика представляет собой науку о методах и средствах распределения состояния технического объекта, включая вопросы организации, контроля, состояния и поиска неисправности, а также принципы построения систем технической диагностики и способа оценки диагностической информации.

Вместе с тем, техническая диагностика является разделом теории надежности.

Основные понятия и определения технической диагностики.

Технический контроль – это проверка соответствия объекта в установленном техническом времени.

Техническое состояние – это совокупность подверженных изменению в процессе функционирования свойств объекта, характеризуемая признаками, установленными нормативно-технической документацией на объект.

Дефект – есть любое несоответствие свойств объекта, заданному требуемому или ожидаемому его свойствам.

Поиск (локализация дефекта) - заключается в указании с определенной точностью его места расположения в объекте.

Лекция № 15.

Поиск (локализация) дефекта – заключается в указании с определенной точностью его места расположения в объекте.

Надежность – это свойство объекта сохранять по времени в установленных пределах все параметры, обеспечивающие выполнение объекта требуемых функций в заданных условиях эксплуатации.

Надежность изделий обеспечивается безотказностью, долговечностью, ремонтопригодностью и сохраняемостью.

Элементы и системы могут находиться в двух состояниях: в работоспособном и неработоспособном.

Работоспособность – это свойство системы или элемента, при котором они способны выполнять задание, сохраняя значения заданных параметров, в установленных пределах.

События, заключающиеся в нарушении работоспособности называется отказом:

Отказы делят:

-Функциональные отказы, при которых объект перестает выполнять свои функции.

-Параметрические отказы, при которых некоторые параметры объекта изменяются в недопустимых пределах.

По причине возникновения отказы бывают:

-Случайные отказы.

-Систематические отказы.

-Конструкционные отказы.

-Технологические отказы.

-Эксплуатационные отказы.

По сложности устранения отказы делятся:

-Устраняемые отказы.

-Не устраняемые отказы.

-Самоустраняющиеся отказы.

Контроль технического состояния представляет собой процедуру определения вида технического состояния объекта, влияющую совокупность операций по проверке технического состояния объекта, включающую совокупность операций по работоспособности, канализации и прогнозированию отказов объекта.

Техническое диагностирование – есть процесс определения технического состояния объекта с определенной степенью точности, произведенной на основе анализа данных, полученных при контроле состояния с целью распознавания вида состояния и места отказа.

Совокупность средств и объекта контроля (диагностирования) и операторов, взаимодействующих с объектом называется системой контроля (диагностирования).

Параметр технического состояния – это физическая величина, характеризующая работоспособность объекта контроля (диагностирования), изменяющегося в процессе ее работы.

Диагностический параметр – это параметр объекта диагностирования, используемый в установленном порядке для определения технического состояния объекта.

Контроле пригодность – это свойство объекта, характеризующее его приспособленность к проведению контроля заданными средствами.

Комплексные показатели надежности:

- коэффициент технического использования равный отношению математического ожидания, времени работоспособного состояния за некоторый период эксплуатации к сумме математических ожиданий, времени работоспособного состояния и всех простоев для ремонта и технического обслуживания

- коэффициент готовности, представляющий собой отклонение математического ожидания времени работоспособного состояния к сумме математических ожиданий этого времени и времени неплановых ремонтов

k Г Т Р Т РТ П

Организация контроля и диагностики сложных технических объектов.

Наиболее общим стандартизированным понятием в области машино- и приборостроения является технический контроль. Объектами контроля могут являться оборудование, продукция, производственные процессы, а также соответствующая техническая документация.

Фактически объектами контроля служат человеко-машинные системы (ЧМС). Всякий контроль обычно осуществляется в два этапа:

1.Получение первичной информации о фактическом состоянии объекта по средствам примирений соответствующих показателей его свойств.

2.Получение вторичной информации о расхождении или не соответствии фактических и требуемых значений, на основе сопоставления первичной информации и заранее установленными нормами.

Процесс измерения в ряде случаев может быть довольно сложным, в частности производится косвенными методами. В общем случае определения характеристик динамических объектов является одной из задач, решаемых методами идентификации. Полученная вторичная информация для выработки регулирующих воздействий на объект, в соответствии с заданной целью управления. Важнейшими понятиями теории надежности технических систем является контроль технического состояния и технического диагностирования, причем первое понятие всегда содержит второе.

Основное назначение операций контроля и диагностирования состоит в повышении надежности объектов на всех этапах их жизненного цикла. Причем диагностирование наиболее важно при эксплуатации. Повышение надежности эксплуатируемого оборудования обеспечивается улучшением таких показателе, как

Коэффициент готовности и технического использования, время восстановления, наработка на отказ и других параметров, путем решения следующих задач:

1.Своевременное обнаружение неисправности.

2.Путем сокращения времени локализации дефектов.

3.Предотвращение отказов.

Результаты контроля и диагностирования сложных объектов используются для прогнозирования их технического состояния. Что позволяет реализовать гибкую систему технического обслуживания и профилактического ремонта.

Классификация средств диагностирования и объектов диагностирования.

Объекты контроля и диагностирования могут быть непрерывными, дискретными и комбинированными, вследствие чего к ним могут применяться различные виды диагностирования: тестовое и функциональное.

Тестовое диагностирование предусматривает подачу на объект из системы контроля специальных тестовых воздействий, причем в этих случаях объект, как правило, не используется по прямому назначению. Каждое очередное воздействие назначается в зависимости от ответов на предыдущее воздействие. Ответы объекта снимают с его основных дополнительных выходных называемые контрольными точками.

Функциональное диагностирование осуществляется в процессе непосредственного использования объекта по его назначению, когда на объект поступает только рабочее воздействие. Данное диагностирование позволяет немедленно реагировать на нарушения функционирования объектов и изменять режим его работы. Недостатком этого вида диагностирования является то, что рабочее воздействие не всегда обеспечивает оптимальность процесса контроля, а также необходимую глубину диагностирования.

Отдельное тестовое или функциональное воздействие и снимаемый с объекта ответ называется единичной проводкой (элементарной) объекта.

Совокупность предписаний о проведении контроля (диагностирования), называется алгоритмом контроля (диагностирования). Алгоритм задает совокупность элементарных проверок, последовательность и реализация и правило обработки результата этих проверок. В результате реализации такого алгоритма получают информацию о работоспособности или неработоспособности исследуемого объекта. При сопоставлении значений диагностируемых параметров с нормативными значениями, получают информацию о характере и месте возможного дефекта, т.е. по причине отказа.

Отказы деталей и узлов различных объектов, в различных условиях, могут иметь совершенно разные последствия.

Эффективность процесса контроля и диагностики определяется не только качеством алгоритмов диагностирования, но и качеством средств контроля диагностирования, которые могут быть следующих видов:

а) По степени охвата: общие и локальные, б) По структурной принадлежности: внешние и встроенные,

в) По степени автоматизации: ручные, автоматизированные и автоматические, г) По спецификации применения: универсальные и специализированные.

Для Объектов повышенной сложности особенно важным является вопрос повышения их контроля пригодности. Уровень контроля пригодности определяет

степень эффективности решения задач диагностирования. Однако требование высокой приборо пригодности усложняет, как проектирование и изготовление соответствующих объектов и ведет к необходимости дополнительных затрат. Поэтому при разработки создания сложных технических объектов, нужны разнообразные подходы и методы для повышения контролепригодности объекта до применяемого уровня.

Таким образом, диагностическое обеспечение закладывается на этапе проектирования объекта, формируется на этапе изготовления и поддерживается на этапе эксплуатации.

Лекция № 16.

Последовательность разработки систем контроля и диагностики СКД.

При разработки СКД необходимо решить комплекс взаимосвязанных задач. Решение этих задач осуществляется в несколько этапов:

1)Исследование объекта контроля, т.е. выяснения принципа его работы, структуры, конструкции и других характерных особенностей.

2)Разработка перечня и классификации возможных дефектов, а также условий

ипризнаков их проявления и анализ способов построения этих признаков в контрольные точки.

3)В случае необходимости решения формализованных задач диагностирования, выбор или построение математической модели объекта, а также соответствующей ей модели диагностирования.

4)Выбор метода и построение алгоритма диагностирования на основе анализа диагностической модели или на основе опыта или интуиции.

5)Оценка качества построенного алгоритма диагностирования. Разработка программно математического обеспечения и выбор средств реализации разработанного алгоритма.

6)Оценка характеристик, выбранных средств диагностирования.

7)Исследование, включая экспериментальные схемы диагностики в целом и при необходимости ее модернизации или доработка, включая ее программное обеспечение.

8)Приемосдаточные производственные испытания СКД.

При разработки СКД, для какого-либо реального объекта, некоторые этапы могут выполняться в ограниченном объекте или вообще отсутствовать.

Структура систем контроля и диагностики (СКД).

Обобщенная структура СКД может быть представлена в виде:

Управляющее

устройство

Генератор

тестов

В общем случае структура СКД предполагает определенную конструктивную принадлежность средств диагностирования. Часть этих средств, с помощью которых оценивается состояние объекта в режиме реального времени обычно встраивается в объект диагностирования. Средства диагностирования, такие, называются встроенными. Другая часть средств диагностирования конструктивно выполняется в виде отдельных самостоятельных блоков и предназначена для выявления некоторых видов отказов на верхних уровнях иерархии СКД. Например, при вычислении интегральных оценок, для формирования и обработки сигнала при тестовых воздействиях, а также для проведения глубокого диагностирования.

Эти средства диагностирования называются внешними.

Как правило, встроенные СКД управляются от микропроцессорного блока самого объекта, а внешнее средство от дополнительного МП. Встроенные и внешние средства диагностирования могут быть классифицированными по их функциональному назначению в соответствии с применяемыми методами контроля и диагностирования и характером контролируемого параметра.

Следовательно, обобщенная функция системы контроля и диагностики включает в себя следующие процедуры:

1)Измерение диагностируемого параметра.

2)Сравнение с нормой и отклонение от нее.

3)Определение причин и места отклонения.

4)Формирование решения по результатам анализа отклонения с точки зрения реакции на обнаруженное отклонение.

5)В общем случае, работа СКД достигается путем использования соответствующего технического и математического обеспечения. Техническое обеспечение СКД основано на примирении различного рода элементов и устройств, разработанных для САУ, которые изучены нами в курсе ЭУСУ.

Математические особенности обеспечения СКД.

Модели объектов и диагностические модели.

Моделирование является одним из инструментов исследований сложных объектов на всех этапах их жизненного цикла. Модель должна с той или иной степенью точности отражать реальный объект или отдельные ее стороны. И позволяет в определенных пределах эмитировать некоторые его свойства. При анализе и синтезе СКД необходимо обеспечить формальное описание проявления тех или иных эффектов в режиме функционирования устройства. Исходной информацией для него служат математическая модель объектов при его нормальном функционировании. Считается, что появление дефектов приводит к изменению параметров модели. Поэтому необходимо конкретизировать характер этих изменений, в случае тех и иных эффектов и учесть их математические модели. Такая модель по своей структуре обычно подобна модели объекта при отсутствии трех дефектов и отличается от ее отдельных компонентов.

Диагностическая модель представляет собой совокупность выбранных методов построения математической модели объекта и методов анализа модели при наличии дефектов, которые определяют специфику построения алгоритмов диагностирования и способы диагностирования.

Диагностическая модель может быть задана в явном или не явном виде.

Явная модель – это совокупность формальных описаний работоспособного объекта, а также всех его возможных неисправностей и неработоспособных состояний.

Неявная модель – это формальное описание объекта математической модели его физических неисправностей и правило получения по этим данным описания других состояний.

Сложные технические объекты, как объекты модернизации обладают структурным и функциональным разнообразием, что и определяет вид соответствующей модели. Можно выделить следующие виды моделей:

1)Непрерывные модели, описывающие состояние объекта непрерывными функциями времени.

2)Дискретные модели, которые определяют состояние объекта в последовательные дискретные моменты времени.

3)Гибридные (комбинированные) модели, описывающие объекты, содержащие устройства как непрерывного, так и дискретного типа.

4)Специальные модели, содержание которых определяется конкретной специальной диагностируемостью обеспечения.

По методам представления взаимосвязей между состояниями объекта, его элементами и параметрами выходных сигналов. Методы построения могут быть разделены на аналитические, графоаналитические, информационные, функционально-логические.

Аналитические модели – позволяют получить соотношение между состояниями объекта диагностируемыми параметрами и показателями качества работы объекта в аналитическом виде.

Графоаналитические методы – представляют собой своеобразные диаграммы, отображающие процессы в объекте и позволяющие выявить некоторые важные диагностирования связи и взаимодействие в объекте.

Функционально-логические модели – это модели, построенные на основе логического анализа функциональных схем изделий.