
лекции / УП_ИДС Игнатьевичь
.pdf
y(t)
t
В связи с этим, большой практический интерес представляет инженерные методы согласования и фильтрации экспериментальных кривых, заданных равно отстоящими дискретными значениями.
yi y(ti )
смежными через интервал
ti ti ti 1
y(t)
t1 |
t2 . . . |
ti-1 |
ti |
ti+1 |
t |
|
|
|
|
|
В настоящее время существует или разработано большое количество сглаженных экспериментальных функций:
-скользящей медианы,
-экспоненциальной,
-рядами Фурье,
-многочленами Чебышева.
Конкретный выбор метода определяется как характером переходной функции и требуемой точности ее определения, так и техническими возможностями инженерного персонала.
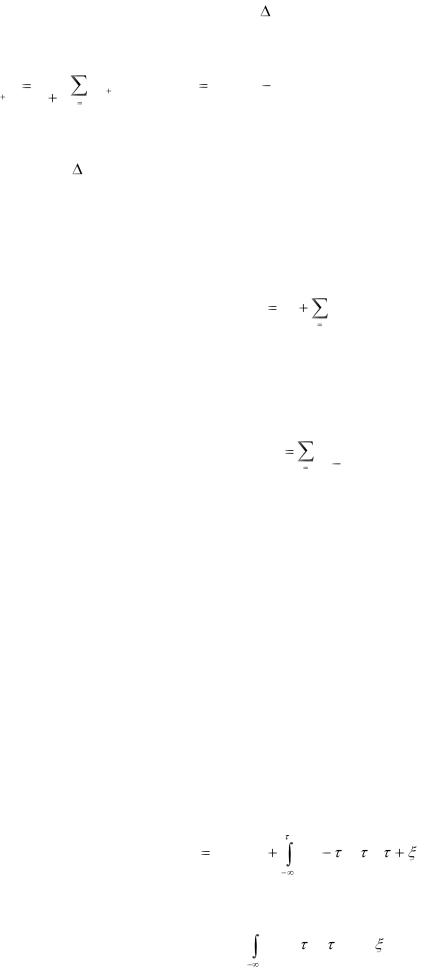
К числу наиболее распространенных методов относится метод скользящих звеньев, который применяется для апериодических переходных функций.
Суть метода заключается в последовательном усреднении ординат yi на
некотором интервале времени равном k t , где k<n и k – четное число. Усреднение выполняется по формуле.
|
|
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
h* |
|
|
|
|
y |
|
|
, |
i 0,1...(т |
k) |
|
|
||
1 |
|
|
|
(i |
m) |
|
|
|||||||
|
k 1 m 0 |
|
|
|||||||||||
(i |
) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
h * |
- ордината оценки переходной функции h(t) . |
|||||||||||||
Интервал k t |
- называют памятью линейного фильтра. |
|||||||||||||
Фильтр такого типа обладает ограниченной полосой пропускания, что |
||||||||||||||
существенно снижает влияние гармонии в исходном процессе. |
||||||||||||||
После выполнения операции сглаживания, экспериментальная кривая |
||||||||||||||
апроксимируется выражение типа. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
e Pi t |
|
|
|
|
|
|
|
|
|
|
h(t) |
c |
0 |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
где c0 - установившееся значение переходного процесса, ci - неизвестные постоянные,
Pi - корни характеристического уравнения динамической системы.
n |
ci P |
|||
|
|
|
||
W (P) |
|
|
|
|
P |
Pi |
|||
i 1 |
||||
Из формулы для h(t) видно, что для ее |
нахождения нужно определить 2n |
|||
значения коэффициентов ci и Pi .
С этой целью применяют специальный метод, основанный на использовании 2n значений экспериментальных функций.
Идентификация по импульсным переходным функциям.
На практике при идентификация динамических систем чаще всего используются импульсные переходные функции W (t) .
Описание объектов с помощью ИПФ имеет ряд преимуществ: минимум априорная информация об объекте, т.е. о структуре параметра, сравнительная простота перехода к другим формам описания динамических систем.
Метод определения ИПФ основан на решении уравнения типа сватки:
h(t) h(0)x(t) |
W (t |
)x( )d |
(t) |
Учитывая, что для физически реализуемых объектов, то
t
y(t)  W (t
W (t  )x( )d
)x( )d (t)
(t)
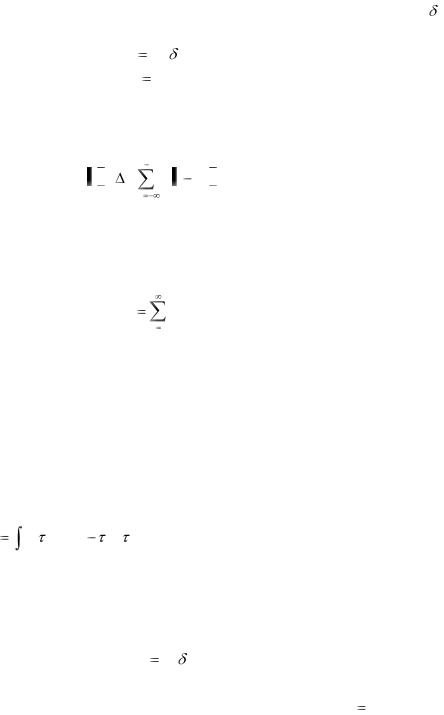
Методы определения ИПФ можно разделить на детерминированные и стохастические.
Детерминированные методы в свою очередь можно разделить на следующие виды:
1) Метод, в котором ИНФ определяется непосредственно как реакция на (t) .
x(t) N0 (t) y(t) N0 w(t)
2) Метод, основанный на аналитическом или численном решении дискретного интегрального уравнения свертки.
n 1
y n  t w n m x[m]
t w n m x[m]
mk
Наиболее просто ИПФ определяется на основе первого метода. Аналитически выражение для
w(t) |
wn |
t n |
|
n! |
|||
n 0 |
|
где wn - определяется через дискретные значения выходного сигнала.
Недостатком детерминированных методов является слабая или низкая помехоустойчивость, что приводит к необходимости использовать статистический
подход к определению w(t) |
ИПФ. |
Стохастические методы в основном корреляционные основаны на решении |
|
уравнения: |
|
|
t |
k yx (t) |
w( )k xx (t )d - уравнение Винера-Хопфа. |
|
0 |
Наиболее просто ИПФ может быть найдено, если в качестве входного сигнала |
|
используется белый шум. |
|
Поскольку АКФ такого сигнала является известной функцией. |
|
|
k xx (t) S0 (t) |
Знание ИПФ позволяет определить передаточную функцию W (t) W (P) . Рассмотренные методы идентификации относятся к тестовым методам.
В ряде случаев, когда отсутствует возможность применения тестового сигнала, поэтому приходится использовать стохастические характеристики, которые присутствуют в процессе естественного функционирования процесса.
При этом задача идентификация разбивается на два этапа:
1.Определение статических характеристик случайных процессов в объекте.
2.Построение модели объектов.
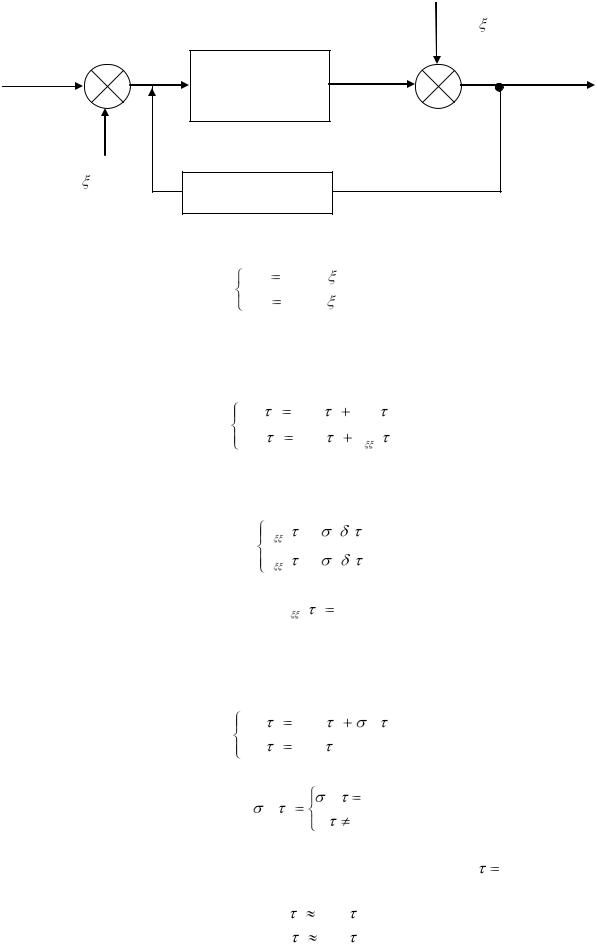
(t)
U(t) |
V(t) |
|
Объект
идентификации
y (t)
(t) |
Коррелометр |
|
x(t) U (t)  (t) y(t) V (t)
(t) y(t) V (t)  (t)
(t)
При отсутствии корреляционной связи помех с входными и выходными сигналами.
k xx ( ) kUU ( ) k ( ) kYY ( ) kUU ( ) k ( )
( ) kYY ( ) kUU ( ) k ( )
Предположим, что помехи представляют собой белый шум. Это означает:
k ( )  k ( )
k ( ) 
2 x
2
U
( )
( )
|
|
|
k |
|
( |
) |
0 |
|
|
|
В таком случае можно записать: |
|
|
|
|
|
|
|
|
|
|
k |
xx |
( |
) |
k |
UU |
( |
) |
2 ( ) |
|
|
|
|
|
|
|
|
|
|
|||
k xy ( |
) |
kUV ( |
) |
|
|
|||||
|
|
2 ( ) |
|
|
|
|
x2 , |
0 |
|
|
|
|
|
|
|
|
0, |
|
0 |
|
|
Что означает, что замена k xx на kUU |
дает ошибку только при |
0 . |
||||||||
|
|
kxx ( |
) |
|
|
kUU ( |
) |
|
||
|
|
kYY ( |
) |
|
kVV ( |
) |
|
|||
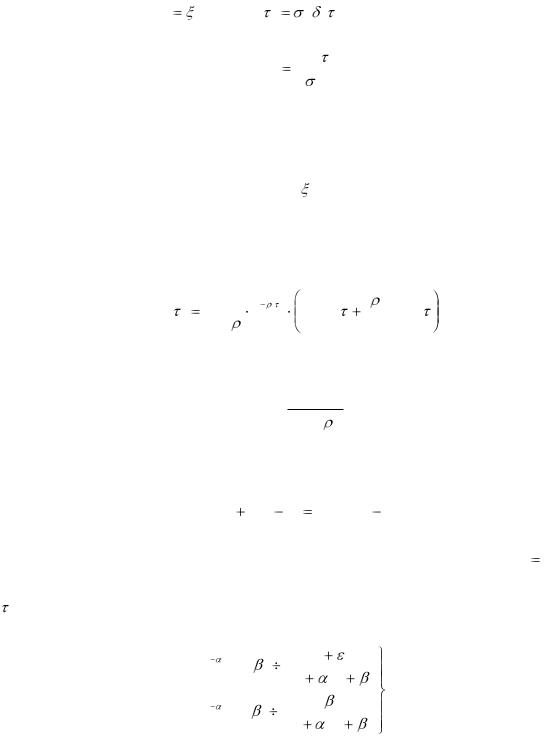
Лекция № 12.
Изложенная выше методика, основанная на применении корреляционного метода позволяет минимизировать влияние помех, причем ошибка идентификации получается тем меньше, чем больше интервал наблюдения стационарного случайного процесса.
Для идентификации импульсных придаточных функций может быть использовано уравнение вида Винера-Хопфа.
Причем наибольшая эффективность идентификации достигается, если в качестве входного сигнала используется сигнал типа белого шума.
Как правило, на практике это условие обычно выполняется поскольку в большинстве случаев можно подобрать воздействие, спектр которого значительно шире полосы пропускания динамической системы.
В этом случае, когда x(t) |
(t) , а k xx ( ) x2 ( |
) , тогда получим: |
||
|
w(t) |
k xx ( |
) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
Рассмотрим применение |
корреляционного метода для определения |
|||
передаточной функции систем, находящейся под воздействием стохастического сигнала типа белый шум.
x(t)  (t)
(t)
Предположим, что зарегистрирована автокорреляционная функция выходного сигнала динамической системы второго порядка, и получено аналитическое выражение вида:
k xx |
( ) |
S |
0 |
e |
|
cos w1 |
|
sin w1 |
|
|
|||||||
4w0 |
|
|
||||||
|
|
|
|
|
w1 |
|||
где w0 - собственная частота динамической системы.
w1 
 w02
w02  2
2
Для вычисления передаточной функции, воспользуемся условием:
k yy (P) k yy ( P) W (P)W ( P)
Если входной сигнал представляет собой белый шум, то величину S0 1.
k yy ( ) можно получить, если воспользоваться соответствием:
e |
t cos |
t |
|
P |
|
|
||
|
|
|
|
|||||
(P |
) 2 |
|
|
|||||
|
|
|
|
|
|
|||
e |
t sin |
t |
|
|
|
|
||
(P |
) 2 |
2 |
||||||
|
|
|
||||||
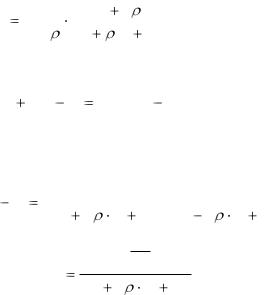
k yy |
(P) |
1 |
|
|
P 2 |
(1) |
|
|
|
|
|
|
|||
4w |
|
(P |
) 2 w2 |
||||
|
|
0 |
|
|
1 |
|
|
k yy (P) k yy ( |
P) |
W (P)W ( P) |
(2) |
||||
Подставим (1) в (2)
k yy |
(P)k yy |
( P) |
w0 |
|
(P 2 2 P w02 )(P 2 2 P w02 ) |
||||
|
|
|
W (P) 
 w0
w0
P 2 2 P w02
Описанная методика применима и в других случаях, когда экспериментальная АКФ апроксимируется другими аналитическими выражениями, допускающие преобразование Лапласа.
Метод идентификации динамических систем, основанный на применении корреляционного анализа имеет следующие достоинства:
1.Вычисление корреляционных функций на достаточно длительном временном интервале, позволяет снизить амплитуду ровного сигнала так, чтобы объект не испытывал существенных возмущений.
2.В ряде случаев, процессы в системе в ходе ее нормального функционирования имеют стохастический характер. Что позволяет вообще обходиться без пробных сигналов.
3.При использовании данного метода не требуется априорных знаний об объекте.
В некоторых случаях входной сигнал не может быть представлен в виде белого шума, численное интегрирование дискретного интегрального уравнения свертки в случае сигналов отличных от белого шума.
В случае сигналов, отличных от белого шума, является практичным, является представление автокорреляционной функции.
И может привести к значительным отклонениям решения задачи идентификации.
Методы идентификации, основанные на аппроксимирующих характеристик объектов.
Всвязи с большими погрешностями решение уравнения Винера-Хопфа возникающие при использовании нестандартных сигналов. Предложены специальные методы построения этого решения с использованием некоторых функционалов.
Вкачестве решения могут быть использованы, так называемые, гладкие решения, получение которых основано на том, что динамические характеристики объектов апроксимируется некоторыми функциями, при этом коэффициенты в этих функциональных выражениях получаются путем обработки входных и выходных сигналов.

При этом точность аппроксимации определяется путем использования критерия близости объекта и модели, которые задаются функционалом ошибки.
При этом задача идентификации распадается на две составляющие:
1.Выбор вида аппроксимирующих функций.
2.Подбор параметров этих функций, причем стараются получить желаемую точность, при как можно меньшем числе используемых функций.
Данный метод базируется на аппроксимации импульсных передаточных функций АКФ, функции обладают тем преимуществом, что позволяет получить достаточно простые алгоритмы идентификации, в том числе и адаптивные.
Метод аппроксимации в теоретическом плане основан на том, что, согласно теоремам математического анализа, любая абсолютно интегрированная на интервале [0, Т] функция f(t), может быть разложена по некоторой системе аппроксимирующих функций.
N |
|
f (t) |
an f n (t) |
n |
0 |
При этом функции f n (t) должны быть интегрируемы, должны быть достаточно
легко реализуемы на ЭВМ.
В качестве такой системы функции могут быть использованы тригонометрические функции, а так же целый ряд специальных полиномов.
Если в процессе идентификации регистрируется импульсная передаточная функция w(t) , то наиболее часто она апроксимируется полиномами Логгера вида:
L |
|
(t) |
|
1 |
|
e |
t |
|
d n |
(t |
n |
e |
t |
) |
|
n |
|
|
n! |
|
|
dt n |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
L0 (t) |
1 |
|
|
|
|
|||||||
|
|
|
L1 (t) |
|
|
t 1 |
|
|
|
|
|||||
L2 (t) |
1 |
t 2 |
|
|
2t 1 и т.д. |
||||||||||
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом на практике число использованных полиномов обычно не превышает
n5 .
Внекоторых случаях экспериментально регистрируется АКФ и ВКФ, допускающих аппроксимацию полиномов Логгера и Чебышева.
Для этих случаев разработан метод типовой идентификации, основанный на том, что с учетом накопленного опыта и теоретических исследований на базе наиболее часто встречающихся входных и выходных сигналов выбирают оператор близких и истинному оператору объекта.
Наличие специальных таблиц типовых идентификаций позволяет определить АКФ и ВКФ в аналитическом виде. Затем из таблиц найти подходящий оператор (в виде диффиринциальных уравнений), а затем определить параметры и другие характеристики модели на основе экспериментальных значений.
Вкачестве типовых входных воздействий наиболее часто используются импульсные воздействия АВФ, который имеет вид:
1) |
k xx (t) |
Ae |
(t ) |
||
|
|
|
|
|
|
2) |
k xx (t) |
Ae (t ) cos wt |
|||
3) k |
xx |
(t) ( A A (t))e t |
|||
|
|
|
|
1 |
|
Рассмотрим метод послужим основой для построения альбомов или атласов типовой идентификации линейных объектов, где а таблицах для наиболее характерных АВК и ВКФ приводятся соответствующие выражения для импульсных передаточных функций, что упрощает и ускорят процедуры идентификации типовых объектов.
Лекция № 13.
Специальные методы идентификации.
1. Идентификация с помощью адаптивных моделей.
Методы аппроксимирующих динамических характеристик объектов, рассмотренные ранее нашли широкое применение при построении адаптивных моделей динамических объектов.
Смысл адаптивных моделей заключаются в том, что такие модели позволяют оперативно подстраивать параметры модели под характеристиками объекта.
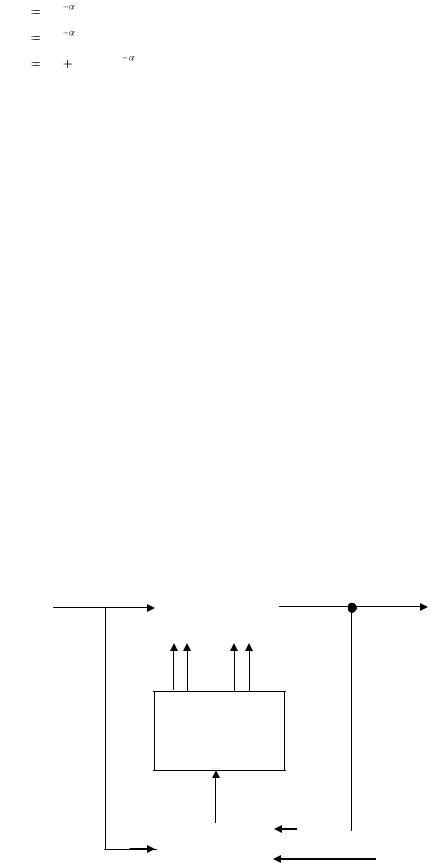
Адаптивная модель может представлять аппаратный либо алгоритмический комплекс, который можно изобразить.
x(t) |
|
YM(t) |
|
Блок анализа |
|||
|
|
||
|
динамических |
|
|
|
характеристик |
|
|
|
|
|
Блок
настраивания
коэффициентов
Блок анализа |
|
Y(t) |
|
||
|
|
|
модели |
|
|
|
|
|
Блок динамических характеристик фактически является собственно моделью объекта представленной, на пример, системой, некоторых ортогональных функций, по которым разложена импульсная передаточная функция.
Блок настраивания коэффициентов - служит для установки коэффициентов модели путем подбора которых достигается требуемая близость выходных координат объекта Y(t) и модели Yм(t).
Блок анализа модели служит для подбора динамических параметров.
Под активной моделью, в соответствии с выбранным алгоритмом поиска экстремума некоторого функционала производится минимализация критерия идентификации, что позволяет получить оптимальную модель объекта. Чаще всего при этом используется поисковые вероятностные интерактивные методы (алгоритмы) градиентного типа (покоординатный метод, градиентный, метод случайного поиска, и т.д.).
Физический смысл итерационных алгоритмов очевиден и заключается в том, что скорость изменения и быстро переменных параметров модели прямо пропорционально модели критерия идентификации.
2. Особенности идентификации не линейных динамических систем.
Очевидно, что идентификация для линейных динамических систем представляет собой весьма сложную задачу. В случае идентификации нелинейных систем трудности не измеримо возрастают.
Как известно, значение параметров нелинейной системы зависят от характеристик входного сигнала, поэтому одной из основных трудностей является, например, выяснение зависимости переходного процесса в системе не только от формы, сигнала, но и от амплитуды входного сигнала, что предъявляет противоречивые требования к выбору тестовых сигналов.
Следующим усложняющим моментом служит большие разногласия типов нелинейности, присущих реальным динамическим системам.
Методы идентификации нелинейных объектов делятся на две основные группы:
1.Методы, основанные на линеаризации математической модели объекта.
2. Методы, в которых модель объекта математическая модель объекта рассматривается как существенно не линейная.
Наиболее полно разработаны методы, относящиеся к первой группе.
Это связано с тем, что такой подход является относительно простым и в ряде случаев обеспечивает желаемую точность.
Однако линеаризованная модель в ряде случаев не является достаточно одекватной и точной.
В некоторых случаях линеаризованная модель может вообще не иметь реального смысла. В этих случаях приходится прибегать к методам идентификации второго пункта.
Методы идентификации принято классифицировать также и по следующим признакам:
1.По наличию априорной информации об объекте. Здесь возникают следующие виды методов:
а) Параметрические методы, в которых известен вид нелинейных зависимостей, но коэффициенты полностью или частично не известны.
б) Прямые методы, в которых априорная информация вообще не существует.
2. По способу представления оператора объекта:
а) Описание по временной области нелинейных уравнений. б) Описание частотной области.
3. По методам восстановления неизвестных параметров нелинейного объекта, к ним относятся:
а) Неитерационные методы. б) Итерационные методы.
При исследовании нелинейных систем определенные сложности возникают также при выборе тестовых сигналов.
Исследованиями установлено, что оптимальным пробным сигналом, каким для линейных систем является гармонический сигнал, для нелинейных систем служит белый шум с дисперсией, превышающей диапазон изменения мощности входного сигнала.
В последнее время вместо дискретного двоичного белого шума для нелинейных систем стали использовать многоуровневые псевдослучайные последовательности. Это вызвано тем, что при увеличении числа уровней свойства дискретного тестового сигнала более адекватны непрерывному реальному белому шуму.
Для аналитического описания нелинейных объектов, были предприняты попытки ввести некоторые обобщенные операторы.
Однако эти операторы не позволяют обосновать все виды нелинейности, поэтому большее распространение получили итерационные методы, в том числе методы стохастической аппроксимации, требующие использования ЭВМ.
С учетом всего сказанного следует иметь в виду, что конкретные пути решения тех или иных задач идентификации практически всегда требуют индивидуального подхода.
Идентификация моделей динамических объектов методами регрессионного анализа.
1. Общие сведения о регрессионных моделях.
При проведении различных исследований различных исследований часто приходится отыскивать и изучать связи между различными процессами и их характеристиками.
Если некоторая величина y однозначна связана с некоторой величиной такая связь называется функциональной, т.е. y  f (x) .
f (x) .
На практике между двумя случайными величинами может существовать стохастическая связь, проявляющаяся в изменении закона распределения этих величин, обнаруживать эту связь удается, как правило, только в результате многочисленных измерений и последующей статической обработки полученных результатов.
Для установления вида зависимости, при стохастической связи величины, т.е. для идентификации этой зависимости используется регрессионный анализ.
При этом различают положительную линейную и нелинейную, отрицательную и неотрицательную регрессии.
