лекции / УП_ИДС Игнатьевичь

На практике каждый реальный объект имеет зоны нечувствительности, гистерезиса и другие нелинейности. В этом случае параметры состояние системы зависят от уровня входного сигнала. Применительно к этому случаю система (3) примет вид:

В случае дискретного линейного нестационарного объекта система (4) может быть записана в виде:

В случае стохастического объекта:

(t) сигнал случайного шума.

Лекция № 6.

Одномерные и многомерные системы.

W(P)

Одномерные

Вопрос о том, что является более приемлемым, а именно: Идентификация с помощью сравнительно простых методов тестовых сигналов или идентификации на основе более усложненных методов без использования тестовых сигналов не имеет однозначного решения и зависит от свойств конкретного объекта, требуемой точности идентификации и технических возможностей экспериментальной аппаратуры.

Тестовые сигналы можно разделить на группы:

-детерминированные,

-стохастические.

Детерминированные сигналы, описываемые тем или иным аналитическим выражением в виде функции времени, бывают трех видов:

1). Ступенчатый сигнал. В частном случае, которого является единичное ступенчатое воздействие:

2). Импульсный сигнал, частным случаем которого является единичное импульсное воздействие:

(t)dt 1

δ(t)

t

3). Гармонический сигнал

x(t)

x0

t

Стохастические сигналы, которые нельзя описывать какими-либо аналитическими функциями времени бывают двух видов:

1). Непрерывные.

2). Дискретные стохастические сигналы – представляют собой последовательность двух сигналов, свойства, которого близки к белому сигналу.

Такие сигналы формируются на основе двоичных сигналов по специальным формулам. Белый шум является, с точки зрения тестирования систем, аналогом детерминированного сигнала в виде функций, причем оба сигнала являются идентифицированными с математической точки зрения и технически не могут быть точно реализуемыми, поэтому на практике используют сигналы близкие к ним по характеристикам.

Свойства и характеристики случайных процессов и случайных величин.

Значение параметров большинства технических систем, характеризующих их состояние, непрерывно изменяются, причем случайным образом относительно их средних значений. Эти изменения имеют случайный характер во времени и называются стохастическими.

Случайные процессы статические характеристики, которых не изменяются во времени, называются стационарными.

Такие процессы позволяют недостаточно длинной реализации определить их статические характеристики и предсказать поведение по времени, т.е. сделать прогноз. Статические характеристики находятся по средствам усреднения значений случайного процесса, либо по времени, если имеется достаточно длительная реализация, либо по множеству реализаций, полученных в пограничные промежутки времени.

Стохастические процессы, для которых результаты его усреднения, полученные в первом и во втором способе равны, называются эргодическими.

Среднее значение:

При вычислении уравнений статистических характеристик случайного стационарного процесса, принято предварительно центрировать этот процесс.

x(t)

Лекция № 7.

Необходимая для расчета линейных систем информация может быть получена на основе корреляционных функций, характеризующих рассматриваемый стохастический процесс. При этом могут быть использованы автокорреляционные или взаимно корреляционные функции.

Автокорреляционные функции стохастического процесса x(t) может быть найдены по формулам:

t – текущее время,

τ – время запаздывания, Т – период.

Физическая величина кхх(τ) показывает на сколько значений стационарного случайного процесса в момент времени t связана с его значением отстоя от t по интервал τ.

Если две величины не зависят дру от друга и их математические ожидания равно 0, то автокорреляционная функция равна 0 (АКФ).

Из функций (15) следуют основные свойства корреляционной функции. 1). Кхх(τ) – четная функция.

2). Кхх(о) – равна среднему значению квадрата отклонения от стационарного случайного процесса от его математического ожидания, т.е. представляет собой дисперсию данного процесса U:

Кхх(0)>0

4). Кхх(τ)→0, τ→∞.

№ 3)и 4) свойства вытекают из определения автокорреляционного из определения автокорреляционной функции, как мера связи двух событий отстающих друг от друга на какой-то интервал времени.

В тех случаях, когда используется связь между двумя стационарными случайными процессами x(t) и y(t), то характеристикой связи между ними является взаимно корреляционная функция.

Основные свойства взаимно корреляционной функции (ВКФ):

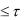0 tk

При t>tk корреляционная функция не выходит за пределы заданного интервала:

k xx ( ) 0,05k xx (0)

Ели текущее значение корреляционной функции отнесем к ее значению при τ=0, то такая корреляционная функция называется нормированной.

В случае если рассматриваемый процесс носит дискретный характер, то автокорреляционная функция:

∆t – интервал дискретизации, m∆t=τ , где m=0,1…N, n=1,2…N

k xx 0,05k(0)

Уравнение (22) будет давать тем большую погрешность вычисления автокорреляционной функции, чем m∆t=τ

m<N/5

АКФ~2%

Это говорит о том, что при фиксированном времени наблюдения, точность вычисления АКФ уменьшается с увеличением времени τ.

На практике вычисление АКФ и ВКФ производит с помощью ЭВМ.

Наряду с использованием корреляционных функций при расчете линейных систем используют преобразование Фурье и получаемые с ее помощью частных частотные характеристики. В этом случае вместо корреляционной функции удобно использовать их преобразования по методу Фурье, называемые спектральной и взаимно спектральной плотностями.

Спектральная плотность мощности (СПМ).

Эта функция является четной функцией частоты w и всегда S(w)>0. Физически эта величина показывает, какая доля мощности случайно стационарного процесса приходится на данную частоту w:

Общая характеристика:

Sобщ 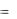S (w)dw

0

С помощью обратного преобразования можно записать:

При прохождении случайного сигнала через линейную динамическую систему его характеристики в общем случае изменяется связь между характеристикой сигнала на входное и выходное может быть выражена в наиболее простой форме, если выражение для СПМ и частотные характеристики для системы. В частности x и y на входе и выходе динамическая система, имеющая W(jw):

Среднее значение M y(t)2 на выходные системы может быть вычислено по формулам:

Если Sxx(w) и W(jw) могут быть выражены рациональными функциями вычисляются с помощью специальных таблиц.

Взаимная спектральная мощность, связанная со специальной плотностью следующими соотношением:

Функция распределения случайной величины может иметь различный характер. В большинстве случаев распределение стационарных процессов подчиняться нормальному распределению.

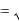
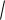x Dx

Лекция № 8.

Характеристики оценки качества и идентификации. Критерии адекватности объекта и модели.

Для решения задач идентификации необходимо ввести некоторый способ оценки в области объекта и описывающей его модели.

Для этого целесообразно воспользоваться выбором некоторого критерия адекватности. На практике наиболее часто принято использовать байсовые критерии минимума среднего риска.

Обозначим у(t) – выходной сигнал объекта, уm(t) – выходной сигнал модели. Рассогласование: (t) .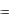

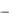Принято оценивать точность идентификации в каждом конкретном случае значением Q(ε) (функция потерь).

Значение величины ε(t) не всегда в равной степени, не во все моменты времени могут быть равноценными, с точки зрения значимости для управления. Поэтому дополнительно вводят функцию значимости: w(t) – функция веса.

Для данной реализации входной величины x(t) качество решения задачи идентификации, в среднем, принято оценивать математическое ожидание функции потерь.

(Q / x) M [q(w, , x)] - средний риск.

Большинство решений задач идентификации являются байсовыми, поскольку получается на основе критерия минимума среднего риска:

k(Q)→min

Вбирая тот или иной вид потерь Q(t) можно получить ряд критериев, применяемых на практике при решении тех или иных задач идентификации.

1). Пусть функция веса w(t)=1. Это означает, что значение ε(t) во все моменты времени равноценны.

Выбираем функцию потерь:

Q( )

0, (t) (t)

Тогда

M [Q( )] 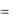( (t) 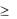(t)) - значение среднего риска.

Это вероятность того, что рассогласование ε(t) выходит за пределы (-φ(t),φ(t)). 2). Пусть Q(ε)=c-δ(ε(t)). Используемую оценку получают критерий

максимального правдоподобия.

Q(ε)=ε2(t) – приходит к критерию средней квадратичной ошибки, применение которого приводит к простым алгоритмам идентификации.

3). Q(ε)=ε(t)

Недостатком, которого является то, что минимум может достигаться не только в точках наибольшей близости у и уm. Но также и в тех точках, где положительные и отрицательные отклонения приблизительно равны. Этого недостатка можно избежать, если взять модель ε(t), т.е.

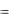
E(t) (t)dt

0

Недостаток оценки: указанный интеграл, оказывается, найти затруднительно. Критерий адекватности могут быть улучшены за счет рационального выбора функций w(t).

Считается удачный выбор функции:

t r0

w(t) e T0

Т0 – наперед заданное времени памяти.

В ряде случаев используют критерии, учитывающий входной сигнал:

В общем случае могут быть использованы также и другие критерии адекватности, причем выбор подходящего критерия адекватности представляет собой в ряде случаев не простую задачу и диктуется во многом особенностями решаемой задачи идентификации. А также уровнем мастерства исследования.

Точность идентификации.