
- •Модели детерминированных сигналов.
- •Случайные сигналы
- •Найходим квадрат модуля частотной характеристики w() 2
- •По выражению находим ординаты спектральной плонтности выходного сигнала.
- •Получаем оценку дисперсии выходного сигнала. Произведя численной интегрирование спектральной плотности по всему значимому диапазону частот выходного сигнала.
- •1. Получение равномерной случайной величины.
- •2. Получение стандартной нормальной случайной величины.
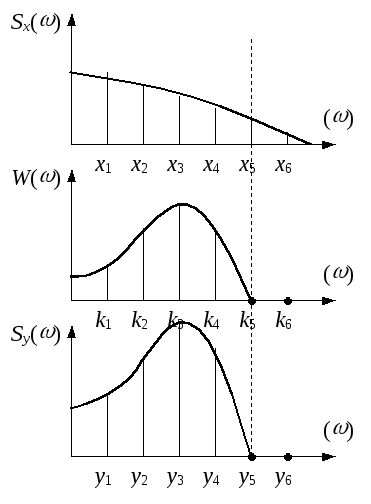
Найходим квадрат модуля частотной характеристики w() 2
По выражению находим ординаты спектральной плонтности выходного сигнала.
Получаем оценку дисперсии выходного сигнала. Произведя численной интегрирование спектральной плотности по всему значимому диапазону частот выходного сигнала.
Данный алгоритм представлен на рисунке.
![]()
![]()
Пусть в качестве динамического звена использовалась передаточная функция системы по возмущению на ошибку системы. После построения алгоритма определения спектральной плотности и дисперсии сигнала на выходе системы можно поставить и решить задачу нелинейного программирования по оптимизации параметров системы с целью минимизации квадратичной ошибки системы.
На основании вышеизложенного модель
случайного сигнала будем задавать в
виде
![]() ,
,
где ,
![]() -
вид закона распределения случайной
величины,
-
вид закона распределения случайной
величины,
![]() - математическое ожидание,
- математическое ожидание,
![]() - дисперсия,
- дисперсия,
![]() - корреляционная функция.
- корреляционная функция.
Получение случайных процессов с заданными характеристиками.
Рассмотрим систему получения класса нормальных случайных процессов с экспоненциальной автокорреляционной функцией, называемых Марковскими. Блок-схема системы, обеспечивающей генерирование Марковских случайных процессов с заданными характеристиками приведен на рисунке. Система включает 3 блока:
- генератор равномерного распределения 1.
- генератор нормального стандартного случайных процессов 2.
- генератор цветного нормального случайного процесса с заданными характеристиками 3.
1. Получение равномерной случайной величины.
Практически во всех языках программирования имеются генераторы случайной величины RND с равномерным распределением от 0 до 1. Случайные величины с данным распределением имеют следующие характеристики:
Мат. ожидание:
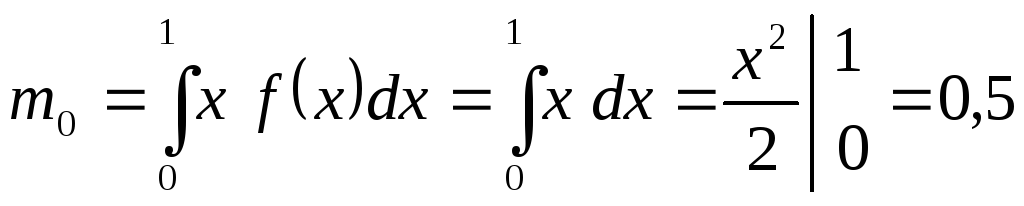 ;
;
Дисперсия :
 .
.
Выход генератора обозначен
![]()
где
![]() -
мат. ожидание
-
мат. ожидание
![]() -
дисперсия.
-
дисперсия.
Временной график и функция распределения данного и других сигналов приведены на рисунке на рисунке .
2. Получение стандартной нормальной случайной величины.
Стандартная случайная величина- это нормальный случайный процесс с нулевым средним и единичной дисперсией N(0,1). В блоке 2 производится суммирование 12 последовательно следующих от генератора N(0,5;1/12) величин для получения одной случайной величины с нормальным законом распределения.
По закону больших чисел случайная величина, на которую влияет большое количество случайных величин с равномерными вкладами и различными законами распределения имеет нормальное (Гауссовое) распределение. Практически уже при 5 - 6 факторах выходная случайная величина имеет нормальный закон распределения. Поэтому полученная сумма имеет нормальное распределение с параметрами:
1. Мат. ожидание:
 ;
;
2. Дисперсия:
 .
.
Для получения нулевого среднего из
суммы вычитается число 6. У полученного
сигнала N(0,1) последующие друг за другом
значения не коррелированы. Его
корреляционная функция не равна нулю
только при
![]() ,
т.е.
,
т.е.
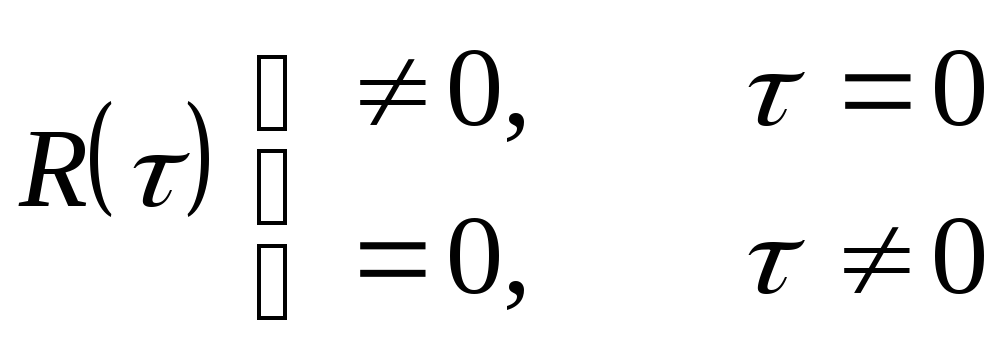 ;
;
Спектральная плоскость данного сигнала
имеет постоянное значение
![]() во всем диапазоне частот
во всем диапазоне частот
![]() .
Это означает присутствие в сигнале всех
гармоник с частотами
.
Это означает присутствие в сигнале всех
гармоник с частотами
![]() .
Сумма цветов видимого спектра света
дает белый свет. Отсюда данный сигнал
получил названиебелый шум.
.
Сумма цветов видимого спектра света
дает белый свет. Отсюда данный сигнал
получил названиебелый шум.
3. Получение нормального случайного процесса с заданными характеристиками производится в блоке 3 путем пропускания стандартного нормального случайного процесса через фильтр первого порядка и смещения случайной величины на величину среднегоа.
Передаточная функция фильтра: Wф (n)
=
![]() ;
;
На выходе блока 3 будет нормальный
случайный процесс хд![]() ,
где
,
где![]() -
среднее и дисперсия полученного сигнала
-
среднее и дисперсия полученного сигнала
![]() - характеризует спектр сигнала.
- характеризует спектр сигнала.
Данный случайный сигнал имеет
экспонинциальную корреляционную
функцию:
![]() .
.
Спектральная плотность сигнала равна:
![]() .
.
Параметры kиТфильтра определяются
из условия получения заданной дисперсии
и корреляционной функцией сигнала:
![]() ;
;
![]() .
.
Выходной сигнал фильтра в разностном виде:
![]() ,
где
,
где
![]() ;
;
![]()
Начальное значение х3 принимается равным 0, тогда:

... и т.д.
Из полученного сигнала отфильтрованы некоторые спектральные компоненты, поэтому он не является белым шумом и называется цветным шумом.
