1. Модели детерминированных сигналов.

1. Виды детерминированных сигналов.

   1. Непериодические детерминированные сигналы. При анализе систем управления используются следующие типовые детерминированные сигналы.

      1. Скачкообразное воздействие. Здесь- единичная функция Хевисайда.

2. Импульсное воздействие. Во временной области импульсное воздействие характеризуется амплитудойАи продолжительностьюимпульса. Математически ипульс характеризуется площадью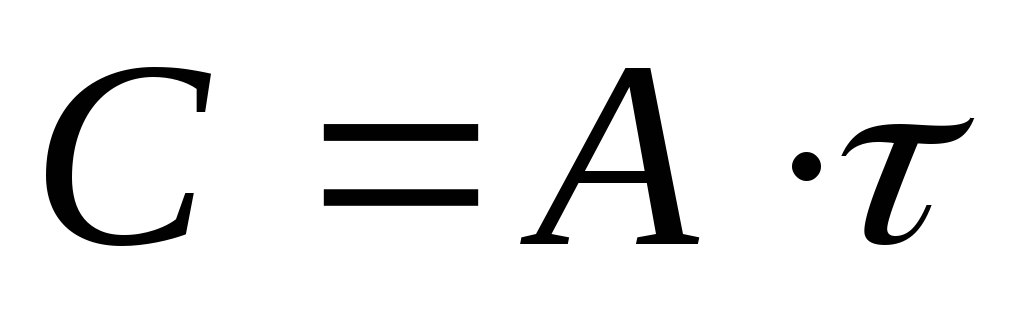и описывается импульсивной функцией- с импульсом С. Здесь- дельта - функция Дирака.

3. 

   Линейное и квадратичное воздействиеи

2. Периодические процессы.

Гармонические процессы - сигналы, содержащиеодну гармонику (например: синусоидальный периодический процесс.

;,.

Полигармонические процессы- периодически несинусоидальные процессыx(t)=x(t+n·T)

Такие процессы являются суммой гармоник, выявление которых производится разложением сигнала в ряд Фурье.

а) Разложение на сумму синусоид и косинусоид:

,.

б) Разложение на ряд сдвинутых по фазе синусоид:

;,

,, n=1, 2, ...

2. Модели детерминированных сигналов.

Выше мы рассмотрели законы изменения детерминированных сигналов во времени. Рассмотрим некоторые другие вопросы, необходимые для описания сигналов.

Применение единичной функции для описания изменения сигналов x(t) во времени. Для задания сигнала необходимо указать:

- время включения сигнала 

- продолжительность действия сигнала

- закон изменения сигнала на отрезке времени от до+

Зададим синусоидальный закон изменения сигнала на заданном отрезке времени

Такое описание требует применение логических функций, что не всегда удобно, например, при необходимости дифференцирования сигнала.

Аналитически время действия сигналов задают с помощью единичной функции Хевисайда 1(t)

Запаздывающая функция Хевайса

Включение сигнала в заданный момент tзаписывается в виде произведения.

дляt = 0дляt = 

Если сигнал подается при t=t₁ и снимается при t=t₂, то используют две функции (разность двух функций 1(t)), например для синусоидального сигнала:

Рассмотрим сигнал

.

При достаточно большой частоте время фронта импульсабудет очень мало по сравнению с временем, существенным для анализа системы. Тогда можно считать, а - т.е. функция Хевисайда, есть идеализация скачкообразного сигнала.

Для скачка амплитудой С .

2.2 Применение импульсных функцийИмпульсными сигналами являются сигналы, продолжительность действия которых мало по сравнению с продолжительностью времени, существенной для анализа системы.

Форму импульса определяет описывающая функция: прямоугольный, треугольный, трапециидальный, синусоидальныйт и др.

Рассмотрим понятие математического импульса.

С математической точки зрения импульс – это интеграл ,

т.е. величина импульса – это площадь под кривой

В дальнейшем надо различать два типа импульсов, как амплитуду временного ряда и математический импульс, как площадь импульса

Рассмотрим гладкий сигнал, возрастающий от 0 до1 за время по любому закону (рис. ). Возьмем производную сигнала и определим ее импульс:

Таким образом, для любой формы сигнала (кривой возрастания) xот 0 до 1 импульс производной равен 1.

Введем дельта функцию Дирака, какпредел

амплитуды производной x(t) при ,т.е ,

т.к. ,

то при , а

Таким образом -функция Дирака имеет две особенности

и ее импульс:

Импульс , а, следовательноx(t)– прямоугольный скачок от 0 до 1, приt = 0, а это функция Хевисайда1(t).Таким образом,(t)есть производная от функции1(t): , и наоборот, .

Модель используется для описания быстро протекающих процессов – взрывов, коротких замыканий КЗ, ударных силовых нагрузок и т.д. При этом ток быстро возрастает до большой величины и быстро падает, а его действие (мощность) имеет конкретное значение. Во втором случае сила за коротное время возрастает от нуля до очень больших значений и снова падет до нуля. Но несмотря на малый отрезок времени воздействие силы совершается определенная работа.

Использование позволяет провести анализ таких ситуаций. При этом имеется определенность во временной области – закон изменения амплитуды во времени, продолжительность действия сигнала. Математический импульс, имеющий физический смысл - мощность, работа и т.д., и количественное значение позволяет проанализировать данные процессы.

Рассмотрим правила действий с использованием -функции Дирака. Чтобы произвести какое-либо действие над-функцией, надо произвести это действие над порождающей ее функциейи взять предел

1. Умножение -функции на константу С. Во временноё области имеет место неопределенностьНайдем импульс произведения

т.е. C^*(t) – есть импульсивная функция с импульсомС (знак * означает импульсивный сигнал). Это важный результат для представления дискретных сигналов.

Размерность произведения при входном сигнале напражение С[в]*[1/сек]=[в/сек].

2. Свойство вырезания. Возьмем импульс от проиведения  (t-τ ) - функции на функциюf(t).

Значение функции f(t)везде кромене имеет смысла, тк произведение

f(t)*равно нулю. Рассмотрим окрестность. Будем считать, что в этом узком диапазоне. Тогда

Отсюда свойство вырезания – значение функции в момент τ равно импульсу произведения функции на дельта функцию Дирака в момент , аналогично при

Отсюда ,

Эти свойства используется при применении принципа суперпозиции в линейных системах и для описания дискретных сигналов

Рассмотрим примеры нахождения произведения и импульса этого произведения:

Если , ,

Для функции f(t)=sin( t) при t=0

f(t)=cos(t) при t=0

f(t)=(t+2) при t=0

при t=1

Отсюда сдвиг аргумента с помощью -функции во временной области:

Примеры применения фунеции Хевисайда и дельта-функции Дирака:

1. Определить

Здесь необходимо определить импульс для функцииЕго значение равно

2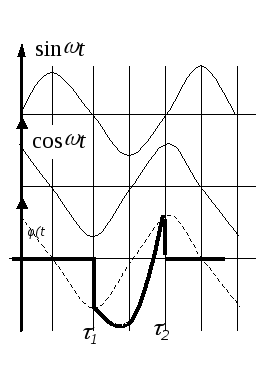. Построить график

f= 50 гц;T = 1/f = 0,2сек;₁= 0,1 сек;₂= 0,2 сек.

• строим график

• вырезаем полученный график от

3. Построить графики функций

Графиком данной функции является последовательность импульсов во времени нулевой длины и бесконечной амплитуды, который не дает информации, связанной с видом функции f(t) во временной области, но импульсы произведения этой функции на дельта-функцию Дирака в каждой точке отсчет равны значениям этой функции в этих точках. Это позвляет использовать дельта функцию для описания дискретных сигналов.

Математические модели дискретных сигналов.

1. Применение - функции для описания дискретных сигналов.

На рисунке представелна последовательность преобразования и представления импульсного сигнала. На рисунке а изображен график непрерывного сигнала. На рис в изображен график реального дискретного сигнала, полученного после прпускания непрерывного сигнала через дискретный ключ (рис б). Дискретизация - это нелинейная операция. Спектральный анализ показывает наличие в полученном импульсном сигнале полезного сигналаx(t)и высокочастотных гармоник. Т.е. дискретизация налагает на полезный сигнал дополнительные шумы. Для их устранения необходимо подобрать такой период дискретизации, чтобы эти шумы отфильтровывались объектом управления или ввести в систему дополнительный элементы, отфильтровывающие полученные компоненты. Рассмотренные выше свойства– функции позволяют описывать дискретные сигналы.

Будем мысленно уменьшать длительность импульса, оставляя его площадь постоянной, равной площади (амплитуде) реального импульсного сигнала.

Тогда длительность модельных импульсов будет стремиться к нулю, а аплитуда возрастать до бесконечного значения и реальный импульсный сигнал можно представить следующей математической моделью

При можно записать

Это обеспечивает и означает

• дает последовательность импульсов во времени

• означает, что импулься этого произведения равны значениям функции в дискретные момены времени

Подразумевая под этими произведениями сами реальные импульсы, запишем временной ряд импульсов

Это гипотетический амплитудно – модулированный импульсный сигнал. При каждом моменте отсчета только одно слагаемое не равно нулю. Этот ряд описывает все множество выборки импульсов.

Обратим внимание, что амплитуда этого ряда не несет информации (см примеры выше). Т.к. здесь есть (t), то график произведенийx(t)(t) в принципе изобразить нельзя, т.к. во всех точках гдепроизведение равно наулю, в противном случае произведение равноили.Об этом говорит и размерность этих произведени, например для электрических импульсов [в] [1/сек] = [в/сек]

Полезную информацию несут импульсы этих произведений. Интеграл от итих произведений рассмотренной суммы равен амплитуде для каждого момента.

2. Применение единичной решетчатой функции.

Введем единичную решетчатую функцию, определяемую следующим выражением

- функция безразмерная.График функции приведен на рисунке. Амплитуда импульсов равна 1.

Использую единичную решетчатую функцию можно описывать импульсные сигналы непосредственно во временной области. Последовательность x(t), равная

с использование единичной решетчатой функции можно записать в виде решетчатой функции x(n):

Если сигнал включен от kдоk + N, то

Таким образом надо различать импульсные сигналы (t) и решетчатые – амплитудные. Импульсные x*(t) – импульсы бесконечной амплитуды, но их импульсы (площади) равны амплитуде полезного сигналвx(n); (размерность(t)– 1/сек; размерностьx(t) - (t)-в/сек)

Решетчатые функции работают непосредственно во временной областпи x(n)– импульсы с амплитудойx(t), разнмерностьx[n] есть размерность самого сигнала, например[в].