Задание 5. Решить задачу Коши:
,
,
,
Составляем характеристическое уравнение и решаем его:
,
,
,
,
.
Общее решение исходного уравнения имеет вид:
.
Находим:
.
Используем начальные условия
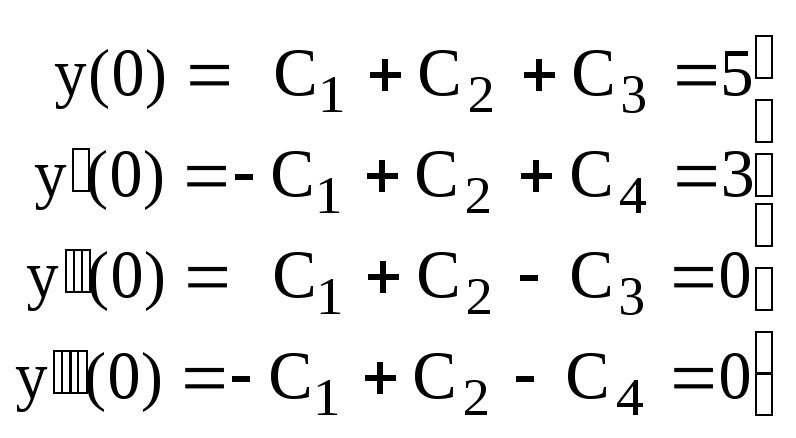
Решаем систему:
,
,
,
.
Решение задачи Коши имеет вид:
.
Задание 6. Найти общее решение:
.
Находим корни характеристического уравнения:
Следовательно общее решение однородного уравнения имеет вид
(
;
—
фундаментальная система решений):
.
Правая часть
уравнения представляет собой сумму
функций
и
.
Для нахождения частных решений, соответствующих этим функциям составляем:
для
S=1 (кратность числа
среди корней характеристического
уравнения)
;
для
:
(кратность числа
среди корней характеристического
уравнения).
т.е.
—
частное решение нелинейного уравнения
с неизвестными коэффициентами.
Подставляем
в исходное уравнение:
Для выполнения тождества необходимо равенство коэффициентов:
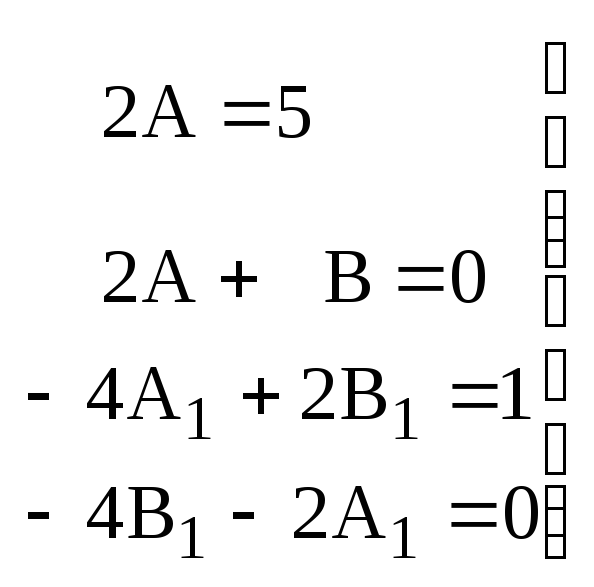
Поэтому:
Таким образом, частное решение исходного уравнения имеет вид:
,
а его общее решение:
Задание 7. Исследовать сходимость числового ряда
.
Решение: Воспользуемся признаком Д'Аламбера:
,
Следовательно,
ряд сходится.
Задание
8. Исследовать сходимость числового
ряда
.
Решение. Применим
радикальный признак Коши:
,
,
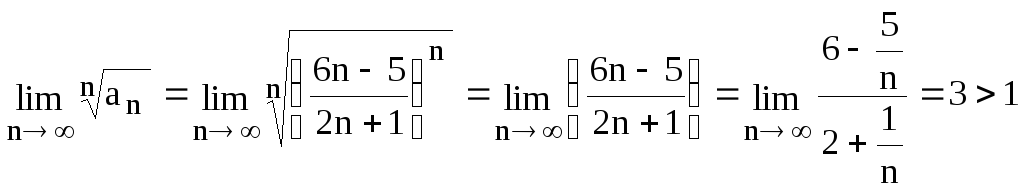т.о. ряд расходится.
Задание
9. Исследовать сходимость числового
ряда
.
Решение. Применим
интегральный признак Коши. Функция
удовлетворяет
условиям признака. Исследуем несобственный
интеграл
.
Т.к. интеграл сходится, то сходится и
данный ряд.
Задание 10. Исследовать сходимость числового ряда.
.
Решение. Воспользуемся предельным признаком сравнения.
Сравним данный
ряд и ряд
,
который расходится.
,
.
.
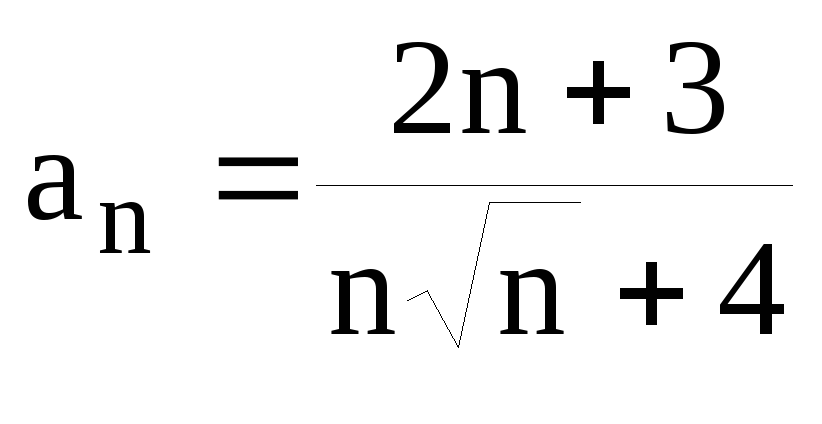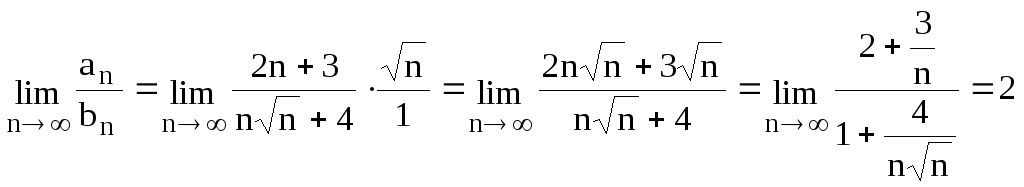Значит, исследуемый ряд расходится, так
же как и ряд
.
Задание
11. Исследовать на сходимость, абсолютную
и условную знакочередующийся ряд
.
Решение. Данный знакочередующийся ряд сходится по признаку Лейбница,
т.к.
и
.
Этот ряд сходится абсолютно, т.к. ряд из
абсолютных величин его членов
сходится по признаку Коши, т.к.
.
Задание
12. Найти область сходимости степенного
ряда
.
Решение. Для
данного степенного ряда вида
,
,
.
Радиус сходимости
.
Следовательно, ряд сходится в интервале
(-3; 3). Исследуем сходимость ряда на концах
интервала. Положим сначала x = 3.
Получим числовой
ряд
,
который расходится (сравним с гармоническим
рядом
).
Возьмем теперь x = -3. Получим
знакочередующийся ряд
,
который сходится условно по признаку
Лейбница
(см. решение примера
6.7.). Таким образом, область сходимости
ряда - полуинтервал
.
Задание 13.
Разложить в ряд
Тейлора функцию
в окрестности точки
.
Найти область сходимости полученного
ряда.
Решение. Искомое
разложение можно найти с помощью формулы
,
положив в ней
и вычислив значения производных функции
при
.
Но проще получить разложение, используя
известное разложение для функции
,
в котором ряд
справа сходится к функции
в интервале (-1,1).
Представим
.
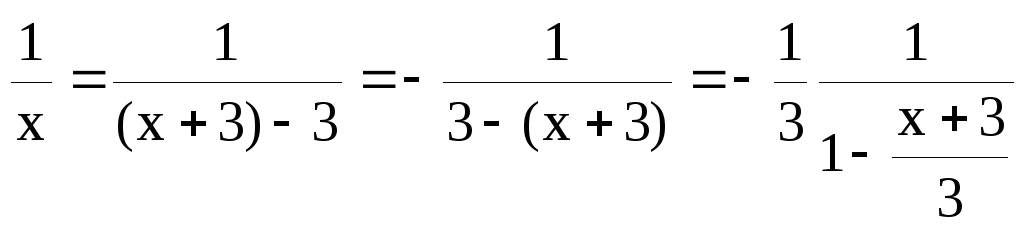Применяя указанное разложение, получим
.
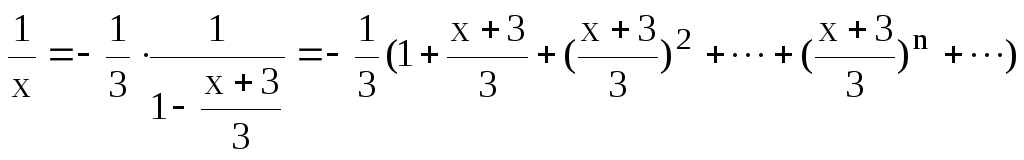Так как, ряд, который
использовали для разложения, сходится
для
,
то данный ряд сходится для
,
отсюда
.
Таким образом, полученный степенной
ряд является рядом Тейлора функции
в окрестности точки
и
его областью сходимости является
интервал (-6,0).