3.5. Логические элементы

3.5.1. Классификация логических элементов

В большинстве современных ЭВМ и цифровых устройствах различного назначения обработка информации производится с помощью двоичного кода, когда информационные сигналы могут принимать только два значения: 1 и 0. Функция двоичных переменных представляет собой логическую, или булеву, функцию , которая, как и ее аргументы, может принимать только два значения – 1 и 0. Логическая функция может быть задана словесно, алгебраическим выражением и таблицей, которая называется таблицей истинности.

Действия над двоичными переменными производятся по правилам логических операций. Между обычной, знакомой нам, алгеброй и алгеброй логики (булевой алгеброй) имеются существенные различия в отношении количества и характера операций, а также законов, которым они подчиняются.

Наиболее часто используются три простейшие логические операции: отрицание (операция НЕ, инверсия), конъюнкция (операция И, логическое умножение) и дизъюнкция (операция ИЛИ, логическое сложение). Более сложные логические преобразования можно свести к указанным выше простейшим операциям. Операция НЕ записывается следующим образом (читается не Х), а элемент, выполняющий операцию НЕ, называют инвертором. Если на входе элемента НЕ Х=1, то сигнал на выходе Y=0, и, наоборот, при Х=0 на выходе получаем Y=1.

На выходе элемента И будем иметь логическую единицу только в том случае, когда на все входы элемента одновременно поданы сигналы, соответствующие уровню 1. Если хотя бы на одном входе элемента – логический 0, то на выходе – также логический 0. Результат операции И очень похож на математическое умножение нулей и единиц, поэтому, по аналогии, операцию И называют логическим умножением. Операция логического умножения И записывается в виде .

Логическая единица на выходе элемента ИЛИ появляется в том случае, когда хотя бы на одном из входов действует сигнал единица. Некоторое сходство результата операции ИЛИ с математическим сложением объясняет применение термина «логическое сложение». Операция логического сложения записывается как .

Широко используются комбинированные логические элементы И-НЕ (элемент Шеффера) и ИЛИ-НЕ (стрелка Пирса), выполняющие логические операции и . Значения выходных сигналов для двухвходовых логических элементов И, ИЛИ, И-НЕ и ИЛИ-НЕ приведены в таблице истинности 3.1.

Таблица 3.1.
0	0	0	0	1	1
0	1	0	1	1	0
1	0	0	1	1	0
1	1	1	1	0	0

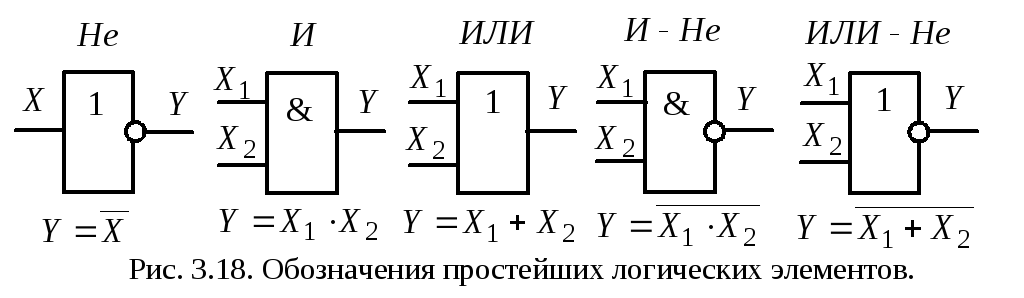
Условное обозначение простейших логических элементов приведено на рис. 3.18.

Элементы И, ИЛИ и НЕ образуют полный базис, т.е. с их помощью можно реализовать любую логическую операцию или функцию. Элемент И-НЕ (как и элемент ИЛИ-НЕ) также образует полный базис. Можно показать, что с помощью только логических элементов И-НЕ можно выполнить все простейшие логические операции: НЕ, И, ИЛИ (рис. 3.19). Реализация основана на известном в алгебре логики законе Де Моргана . Аналогично, операции НЕ, И, ИЛИ можно реализовать, используя комбинированные логические элементы ИЛИ-НЕ.

По способу кодирования информации различают потенциальные и импульсные логические элементы. Информация, обрабатываемая потенциальными логическими элементами, характеризуется отличающимися потенциальными уровнями. Если логической единице соответствует высокий потенциальный уровень, а логическому нулю – низкий, то такую логику называют положительной (позитивной). Наоборот, если логической единице соответствует низкий потенциальный уровень, а логическому нулю – высокий, то говорят об отрицательной (негативной) логике. В импульсных логических элементах логической единице соответствует наличие импульса, а логическому нулю – его отсутствие.

Логические элементы классифицируют также по типу применяемых транзисторов. Наибольшее распространение получили ЛЭ на биполярных транзисторах и полевых МДП-транзисторах. Цифровые интегральные микросхемы выпускаются сериями, внутри каждой из которых имеются объединенные по функциональному признаку группы устройств: логические элементы, триггеры, счетчики, регистры и т.д. Чем шире функциональный состав серии, тем большими возможностями может обладать цифровое устройство, выполненное на базе микросхем данной серии. Микросхемы, входящие в состав каждой серии имеют единое конструктивно- технологическое исполнение, единое напряжение источника питания, одинаковые уровни сигналов нуля и единицы. Все это делает микросхемы одной серии совместимыми. Основой каждой серии цифровых микросхем является базовый логический элемент. Как правило, базовые логические элементы выполняют операции И-НЕ либо ИЛИ-НЕ и по принципу построения делятся на следующие основные типы, широко применяемые в настоящее время: элементы диодно-транзисторной логики (ДТЛ), транзисторно-транзисторной логики (ТТЛ), эмиттерно-связанной транзисторной логики (ЭСТЛ), интегральной инжекционной логики (ИИЛ), логические элементы на комплементарных МДП-транзисторах (КМДП-логика).