4.3. Вимушені електричні коливання

Електричний опір R будь-якого реального коливального контуру відмінний від нуля. Тому вільні електричні коливання в контурі поступово затухають. Щоб одержати незатухаючі коливання, треба ззовні підводити в коливальний контур енергію, яка компенсує втрати на виділення ленц-джоулевої теплоти. В цьому випадку виникають не вільні, а вимушені електричні коливання. Для їх реалізації потрібна періодична дія на коливальний контур. Це можна здійснити, якщо ввімкнути послідовно з елементами контуру зовнішню змінну напругу U=U_mcosωt.

Тоді рівняння (4.11) набирає вигляду

Виконавши незначні перетворення, отримаємо рівняння

(4.25)

Тут β і ω_о визначаються за формулами (4.12) та (4.5). Рівняння (4.25) називають диференціальним рівнянням вимушених коливань, яке є неоднорідним рівнянням другого порядку. Загальний розв’язок такого рівняння складається із суми розв’язків відповідного однорідного рівняння (4.13) і частинного розв’язку неоднорідного рівняння (4.25). Розв’язком відповідного однорідного рівняння є затухаючі коливання (4.14). Тому через порівняно короткий час після початку коливань впливом цього доданка на загальний розв’язок рівняння (4.25) можна нехтувати. Частинний розв’язок рівняння (4.25) шукатимемо у вигляді

(4.26)

де q_m –амплітуда усталених коливань; φ – зсув фаз між змінами заряду і зовнішньою напругою. Для того, щоб рівняння (4.26) було частинним розв’язком рівняння (4.25), необхідно значення із (4.26) підставити в (4.25). Виконавши математичні перетворення, одержимо

(4.27)

(4.28)

Рівняння (4.27) та (4.28) можна записати по аналогії з подібними для механічних затухаючих коливань.

Підставивши у формули (4.27) і (4.28) ω_о² із (4.5) і 2β із (4.12), одержимо

(4.29)

(4.30)

Отже, частинним розв’язком рівняння (4.25) і рівнянням усталених вимушених коливань є рівняння

(4.31)

Розділивши заряд q на ємність С конденсатора, одержимо закон зміни напруги на конденсаторі

де (4.32)

Диференціюючи за часом рівняння (4.31), одержуємо закон зміни струму в коливальному контурі

.

Амплітуда сили струму виражається формулою

. (4.33)

Залежність амплітуди вимушених коливань від частоти змушувальної сили (зовнішньої напруги) призводить до того, що за деякої певної частоти амплітуда коливань досягає максимального значення. Це явище називають резонансом, а відповідну частоту ω_рез – резонансною частотою.

Дослідивши рівняння (4.27) і (4.37) на екстремум знаходимо, що резонансна частота для заряду q і напруги на конденсаторі U_c визначається так:

(4.34)

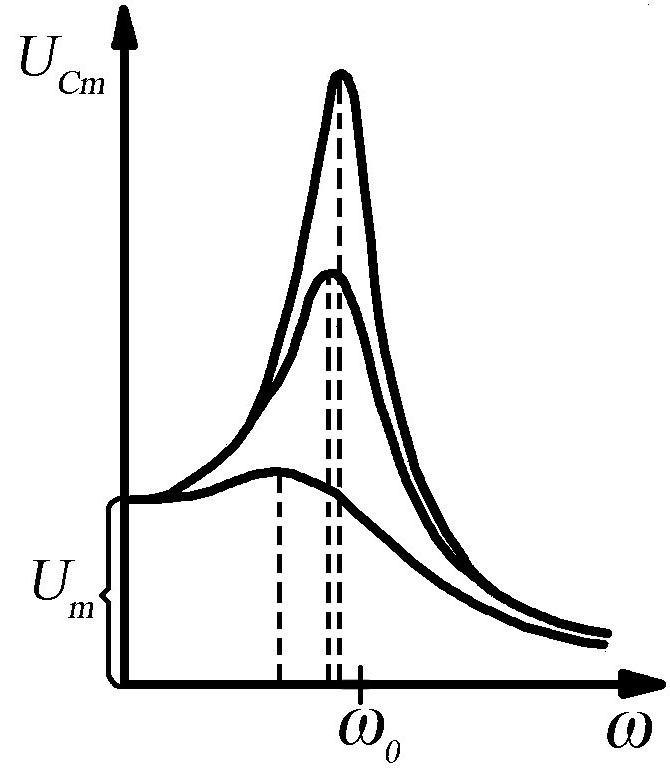
Резонансні криві для U_c зображені на рис. 4.4.

При ω→0 резонансні криві сходяться в одній точці з ординатою U_cм=U_m – зовнішній напрузі в мить під’єднання конденсатора до зовнішнього джерела. Максимум є тим більшим і гострішим, чим менше значення тобто чим менший активний опір і більша індуктивність контуру.

При малому затуханні (при β²<<ω_o²) резонансну частоту для напруги можна прийняти як такою, що дорівнює ω_o. Тоді, згідно з (4.32), відношення амплітуди напруги на конденсаторі при резонансі U_mсРЕЗ до амплітуди зовнішньої напруги U_m буде дорівнювати

(4.35)

Тут Q – добротність контуру. Таким чином, добротність контуру показує у скільки разів напруга на конденсаторі може перевищувати прикладену напругу.

Із (4.33) знаходимо, що амплітуда сили струму досягає максимального значення за умови . Отже, резонансна частота для сили струму співпадає з власною частотою контуру ω_o:

(4.36)

Резонансні криві для сили струму зображені на рис4.5.

Рис.4.4 Рис4.5 Рис.4.6

Однією з характеристик резонансної кривої є значення амплітуди у максимумі. Другою важливою характеристикою є ширина резонансної кривої, під якою розуміють різницю циклічних частот для яких енергія коливань є у два рази меншою від енергії частоти, при якій амплітуда змінної величини досягає максимуму. Оскільки енергія коливань пропорційна квадрату амплітуди (W~A²), то очевидно, що ширина резонансної кривої, яка відповідає вимогам W/W_рез=0,5, визначається відношенням амплітуд A_m/A_mрез=0,7 (див. рис.4.6для резонансної кривої струму).

Можна показати (див. [5]), що ширина резонансної кривої зв’язана з добротністю коливального контуру співвідношенням:

Явище резонансу використовують для виділення із складної напруги потрібну складову. Нехай напруга, прикладена до контуру, дорівнює

Настроївши контур на одну із частот ω₁, ω₂ ... (тобто підібравши відповідним чином параметри C і L), можна отримати на конденсаторі напругу, що в Q разів перевищує значення даної складової, в той час як напруга, створена на конденсаторі іншими складовими, буде слабкою. Так, наприклад, можна настроїти радіоприймач на бажану довжину хвилі.