Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Регрессионной анализ

Методическое указание к выполнению лабораторной работы

по дисциплине “Идентификация и диагностика систем управления”

для студентов специальности 220201

всех форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2010

Цель работы: Освоение регрессионного анализа в пакете EXCEL.

ОСНОВНЫЕ ПОНЯТИЯ

Задачами регрессионного анализа являются: установление формы зависимости между переменными, оценка функций регрессии, оценка неизвестных значений зависимой переменной (прогноз).

Односторонняя зависимость случайной зависимой переменной Y от одной или нескольких независимых переменных Х называется объясняющей регрессией. Такая зависимость может возникать тогда, когда при каждом фиксированном значении X, соответствующее значение Y подвержено случайному разбросу под воздействием неконтролируемых факторов. Такая зависимость Y(X) называется регрессионной. Она может быть представлена в виде модельного уравнения регрессии:

(1)

где - случайная переменная характеризующая отклонение функции регрессии.

Линейный регрессионный анализ - это анализ, для которого функция f(X) линейна относительно оцениваемых факторов. Уравнение линейной регрессии имеет вид:

(2)

Регрессионный анализ включает в себя две основные компоненты:

1) оценка вектора коэффициентов с помощью метода наименьших квадратов: ;

2) дисперсионный анализ.

Для проведения регрессионного анализа необходимо:

1. чтобы количество экспериментальных данных было больше либо равно 30 на один вход;

2. распределение выходной величины должно быть нормальным;

3. в процессе эксперимента дисперсия выходной величины Y не меняется: ;

4. переменная X является детерменированой;

5. выходные переменные Y₁, Y₂, … Y_n стохастически независимы между собой: ;

6. дискретность проведения экспериментов во времени берется таким образом, чтобы последовательно взятые значения Y₁, Y₂, … Y_n были стохастически независимы, то есть больше времени затухания автокорреляционной функции;

7. учет динамики в регрессионном анализе производится в виде транспортного запаздывания, которое определяется как время нахождения максимума взаимно корреляционной функции X и Y.

На основании этих предпосылок получают уравнение регрессионной модели методом наименьших квадратов.

Задача дисперсионного анализа заключается в определении той части экспериментальных данных, которая описывается регрессионной моделью (определяется коэффициент детерминации R² ), а также определение адекватности регрессионной модели. Для этого используется основное уравнение дисперсионного анализа, которое имеет вид:

(3)

где - полная сумма квадратичных отклонений характеризует разброс значений выходной величины y вокруг его среднего значения ; - остаточная сумма отклонений используется в качестве критерия МНК; - сумма квадратичных отклонений расчетных значений выходной величины от среднего значения .

Коэффициент детерминации R² определяется соотношением суммы обусловленной регрессией и остаточной суммы отклонений:

(4)

Коэффициент детерминации изменяется от 0 до 1:

При коэффициент детерминации а при коэффициент детерминации . Чем ближе коэффициент детерминации к 1, тем точнее регрессионная модель.

При малых объемах выборки (N<30) используется коэффициент множественной корреляции:

, (5)

где N – количество выборки; m – количество входов.

Для оценки адекватности регрессионной модели используется критерий Фишера, который определяется отношением дисперсии обусловленной регрессией и остаточной дисперсией:

, (6)

Дисперсия, обусловленная регрессией - среднее значение квадратов отклонения обусловленных регрессией, определяется выражением:

(7)

где f_р - число степеней свободы суммы обусловленной регрессией:

_{, (8)}

где m – количество входов.

Остаточная дисперсия определяется выражением:

(9)

где f_ост - число степеней свободы остаточной суммы:

_{, (10)}

где N - число экспериментов, m – количество входов.

Для определения адекватности регрессионной модели сравнивают F-отношение, рассчитанное по выражению (6), со значением критерия Фишера выбранного из таблиц для принятого уровня значимости и числа степеней свободы сравниваемых дисперсий и _.

Если , то при соответствующем уровне значимости регрессионная модель не адекватна.

Если , то при соответствующем уровне значимости регрессионная модель адекватна.

Результаты дисперсионного анализа сводятся в таблицу 1.

Таблица 1. Дисперсионный анализ

	f	SS	MS	F	P- знач	F крит
регрессия
остатки
Итого

Интерпретация результатов:

SS - сумма квадратов; f - число степеней свободы; MS - средний квадрат отклонений (дисперсия); F- расчетное значение отношения Фишера; P-уровень значимости для вычисленного значения F; F_криm - табличное значение отношения Фишера.

Если регрессионная модель адекватна, определяют значимость коэффициентов регрессии. Для проверки значимости анализируется отношение коэффициента регрессии и его среднеквадратичного отклонения. Это отношение является распределением Стьюдента, то есть для определения значимости используем t – критерий:

(11)

где _i - значение коэффициента, - среднеквадратичное отклонение коэффициента.

Для определения значимости коэффициента сравнивают расчетное и табличное значение t – критерия. Табличное значение t – критерия определяется степенью свободы и значением заданной вероятности Р : t_таб (, Р).

Если t_рас>t_таб, то коэффициент b_i является значимым.

Доверительный интервал определяется по формуле:

. (12)

Если коэффициент регрессии незначим, то соответствующий ему входной фактор несущественно влияет на выходную величину и его можно исключить из регрессионной модели.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Исходные данные взять в таблицах(2,3) согласно варианту (по номеру студента в журнале).

2. Ввести исходные данные в таблицу в пакете Excel.

3. Подготовить два столбца для ввода расчетных значений Y и остатков.

4. Вызвать программу «Регрессия»: Данные/ Анализ данных/ Регрессия. Диалоговое окно «Анализ данных» представлено на рисунке 1.

Рис. 1. Диалоговое окно «Анализ данных».

5. Ввести в диалоговое окно «Регрессия» адреса исходных данных:

• в опцию « входной интервал Y» ввести адреса ячеек столбца выходной величины Y,

• в опцию «входной интервал X» ввести адреса ячеек столбца входной величины X,

• установить уровень надежности 95%,

• в опции «Выходной интервал», указать левую верхнюю ячейку места вывода данных регрессионного анализа,

• включить опции «Остатки» и «График остатков»,

• нажать кнопку ОК для запуска регрессионного анализа. Диалоговое окно «Регрессия» представлено на рисунке 2.

Рис. 2. Диалоговое окно «Регрессия».

6. Excel выведет четыре таблицы и два графика зависимости остатков от переменных Х1 и Х2.

7. Построить графики для Y_эксп, Y_расч и график ошибки прогноза (остатка).

8. По полученным графикам оценить правильность модели по входам Х1, Х2.

9. Рассчитать коэффициент множественной корреляции, расчетные значения t-критериев, доверительные интервалы коэффициентов регрессии по выражениям (5,11,12).

10. Сделать выводы по результатам регрессионного анализа.

11. Подготовить отчет по работе.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Результаты регрессионного анализа представлены на рисунке 3.

Графики зависимости остатков от переменных Х1 и Х2 представлены на рисунке 4.

Графики расчетной и экспериментальной выходной величины, и график ошибки прогноза представлены на рисунке 5.

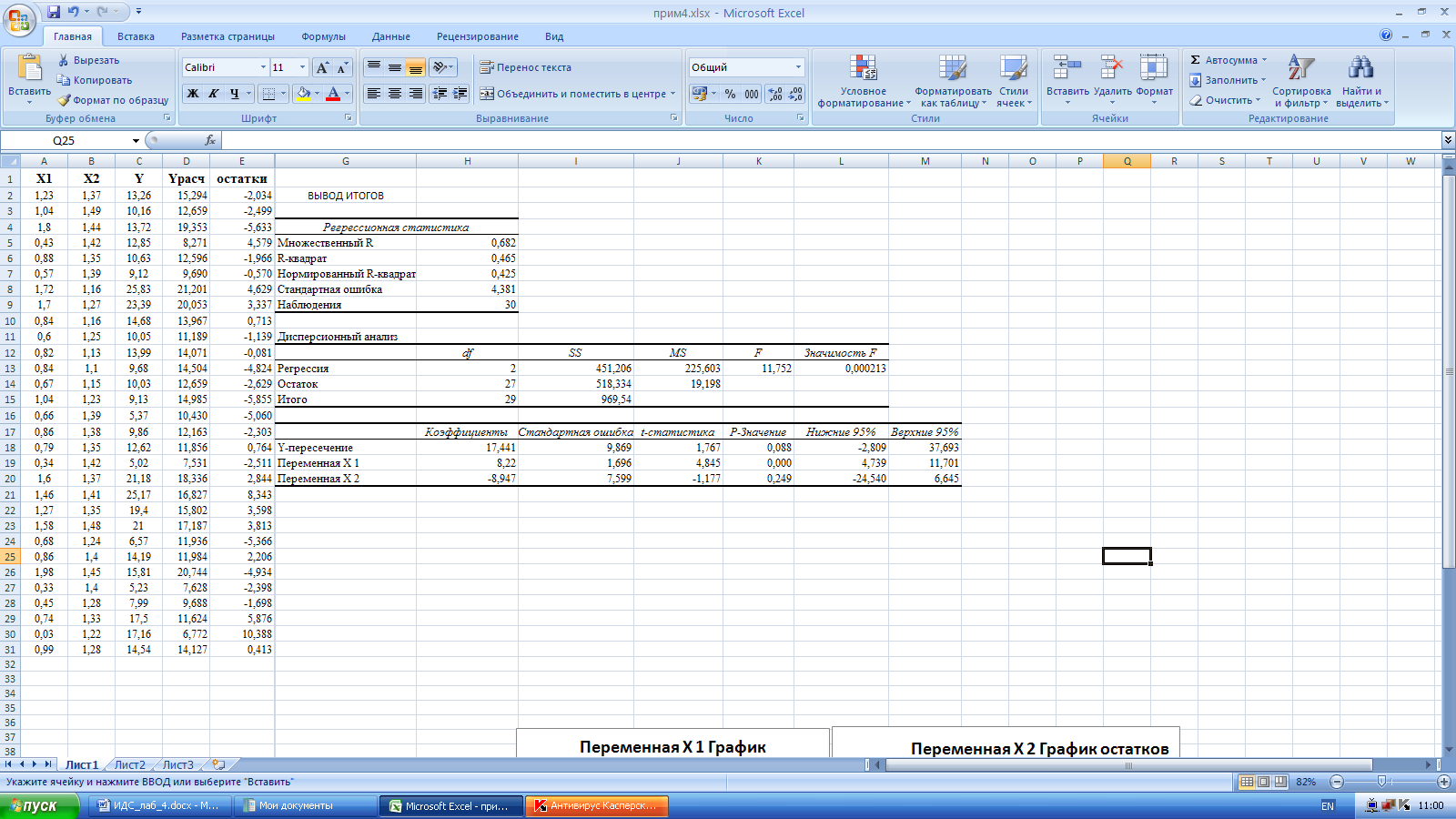
Рис. 3. Пример регрессионного анализа в пакете EXCEL

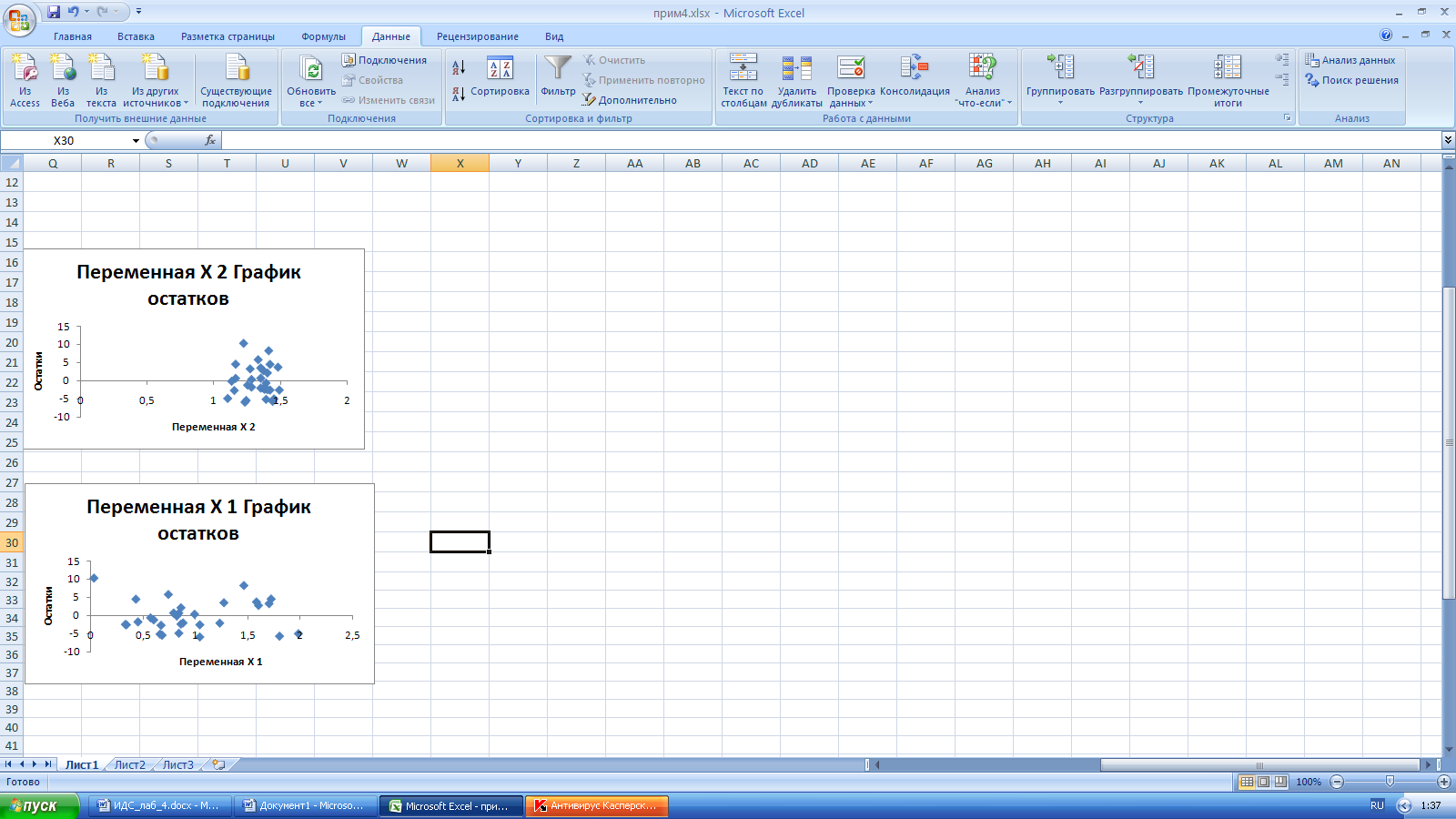
Рис.4 . Графики остатков переменных Х1, Х2

Рис. 5. Графики Y_эксп, Y_расч и ошибки прогноза (остатки).

По результатам регрессионного анализа можно сказать:

1. Уравнение регрессии полученное с помощью Excel, имеет вид:

2. Коэффициент детерминации:

Вариация результата на 46,5% объясняется вариацией факторов.

3. Коэффициент множественной корреляции:

4. Проверка на адекватность модели. Анализ выполняется при сравнении фактического и табличного значения F-критерия Фишера.

Фактическое значение F-критерия Фишера превышает табличное - модель адекватна.

5. Проверка значимости коэффициента b_0.

Расчетное значение t-критерия для коэффициента b₀:

Табличное значение t-критерия t_таб. (29, 0.975)=2.05

6. Доверительный интервал коэффициента b₀:

7. Проверка значимости коэффициента b_1.

Расчетное значение t-критерия для коэффициента b₁:

t_рас.>t_таб., коэффициент b₁ является значимым

8. Доверительный интервал коэффициента b₁:

9. Проверка значимости для коэффициентаb₂.

Расчетное значение t-критерия для коэффициента b₂:

t_рас.<t_таб., коэффициент b₂ является не значимым, значит фактор X 2 незначительно влияет на выходную величину Y, и его можно исключить из уравнения регрессии.

10. На основании анализа значимости коэффициентов уравнение регрессии примет вид: