Построение нелинейной одномерной модели методом наименьших квадратов

Цель работы - освоение метода построения нелинейной модели с применением линеаризации; освоение метода оценки адекватности модели и ошибки аппроксимации; автоматизация процесса построения математи­ческой модели; освоение основных приемов работы в электронных табли­цах EXCEL.

ОСНОВНЫЕ ПОНЯТИЯ

Под нелинейной регрессией понимают более сложную односторон­нюю стохастическую зависимость. Наиболее часто встречаются следую­щие виды нелинейной регрессии:

Полиноминальное уравнение регрессии:

, (7)

Гиперболическое уравнение регрессии:

, (8)

Степенное уравнение регрессии:

. (9)

Могут применяться показательные, логарифмические, триго­нометрические уравнения, а также полиномы Чебышева.

Обычно подбор конкретной функции осуществляется на базе той науки в рамках которой изучается данный процесс.

Принято различать два класса уравнений нелинейной регрессии.

Первый класс охватывает регрессии нелинейные относительно входного параметра х, но линейные относительно коэффициентов . Для таких регрессий применим метод наименьших квадратов.

Второй класс охватывает регрессии, которые являются нелиней­ными также относительно коэффициентов , что требует для применения итерационных методов.

Достаточно часто в различных технических исследованиях используется параболическая регрессия к-го порядка.

Для случая к=2 такая регрессия имеет вид:

(10)

В этом случае для нахождения коэффициентов составляется система трех уравнений:

(11)

Необходимо иметь в виду, что после вычисления коэффициента все­гда должна осуществляться проверка их значимости по соответствую­щей методике и незначимые коэффициенты обнуляются.

При использовании степенного уравнения регрессии следует иметь в виду, что оно нелинейно относительно параметров , однако путем лога­рифмирования может быть преобразовано в линейное уравнение:

(12)

Для определения неизвестных параметров ,,…используется ме­тод наименьших квадратов.

Построение нелинейной модели путем линеаризации

Рассмотрим пример линеаризации степенного уравнения:

. (13)

Проведем логарифмирование и получим:

. (14)

Введем обозначения:

; ;;.

Получили линейное регрессионное уравнение:

(15)

Коэффициенты ,мы имеем определенные:

и , (16)

но вместо экспериментальных данных необходимо использовать и.

Получив оценки коэффициентов и _, по выражениям (10) находим коэффициенты a и b исходного уравнения (7).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ

Задан нелинейный статический объект с 1 входом и 1 выходом. Вы­ход объекта измеряется со стационарным некоррелированным шумом. Имеется выборка пассивного эксперимента объемом 21 точка, содержащая значения входной и выходной переменных с дискретностью dt=1.

1. Разработать в электронных таблицах EXCEL программу для реше­ния поставленной задачи, выбрать вид уравнения аппроксимации, опреде­лить коэффициенты уравнения и ошибку аппроксимации.

2. Ввести наименование работы, фамилию студента, номер варианта работы.

3. Подготовить шапку таблицы и таблицу, включающую: номера точек по порядку, значения входной переменной, значения выходной переменной, преобразованные переменные, расчетные значения выходной переменной, столбец расчета ошибки аппроксимации, ячейки для коэффициентов нелинейного и линеаризованного уравнений, ячейки для ошибки аппроксимации.

4. Построить экспериментальный график зависимости y=f(x) выход­ной переменной от входной переменной.

5. Провести анализ графика и подобрать вид нелинейного уравнения (используя справочную литературу).

6. Подобрать закон преобразования переменных y и x в y^* и x^* , чтобы получить линейное уравнение.

7. Рассчитать преобразованные переменные y^* и x^* .

8. Найти коэффициенты ,и уравнение

9. Построить график зависимости y^*=f(x^*) преобразованных перемен­ных.

10. Построить график зависимости y^*=f(x^*).

11. Построить линейную линию тренда и ее уравнение с заданным ко­эффициентом детерминации R².

12. Проанализировать результаты на смещение, разброс точек.

13. Рассчитать коэффициенты для нелинейного уравнения a и b исход­ного нелинейного уравнения.

14. Рассчитать y и построить график y_расч=f(x) по нелинейному уравне­нию.

15. Рассчитать ошибку аппроксимации:

(17)

По положению расчетной кривой на экспериментальных данных и величине остаточной ошибки оценить правильность выбора уравнения аппроксимации.

16. Отформатировать все элементы таблицы и графики.

ПРИМЕР ЛАБОРАТОРНОЙ РАБОТЫ

П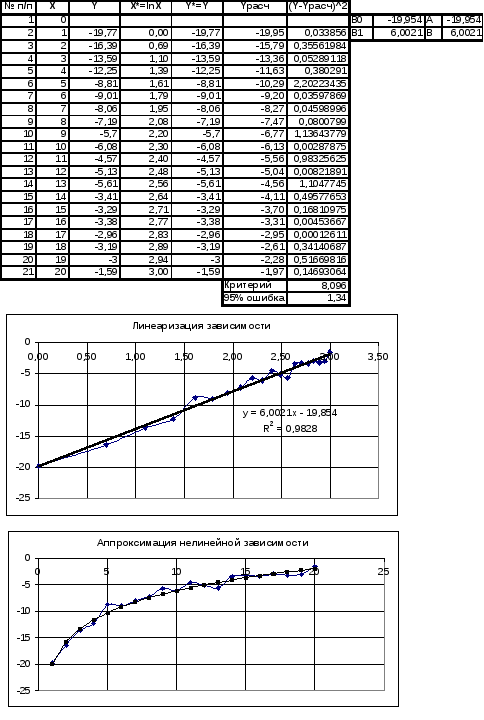ример построение нелинейной модели методом наименьших квад­ратов представлен на рисунке 2.

Рис. 2. Построение нелинейной модели методом наименьших квадратов

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА

Отчет оформляется в текстовом редакторе Word на бумаге формата А4 ГОСТ 6656-76 (210х297 мм) и содержит:

5. Название лабораторной работы.

6. Цель работы.

7. Задание.

8. Результаты вычисления.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Что понимают под нелинейной регрессией?

2. Какие существуют классы нелинейной регрессии?

3. Какие существуют виды нелинейной регрессии?

4. Для какого класса регрессий применим МНК?

5. Вид уравнения параболической регрессии к-го порядка.

6. Вид гиперболического уравнения регрессии.

7. Вид степенного уравнения регрессии.

8. Привести пример линеаризации степенного уравнения.

9. Как строится линейная линия тренда и находится ее уравнение с за­данным коэффициентом детерминации R?

10. Как определить количественную оценку точности аппроксима­ции?

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ

ЛАБОРАТОРНОЙ РАБОТЫ

Подготовка к работе – 0,5 акад. часа.

Выполнение работы – 0,5 акад. часа.

Расчеты на ЭВМ – 0,5 акад. часа.

Оформление работы – 0,5 акад. часа.

ЛитЕратура

4. Идентификация объектов управления: учеб. пособие. / А. Д. Семенов, Д. В. Арта­монов, А. В. Брюхачев. - Пенза: ПГУ, 2005. - 211 с.

5. Основы теории идентификации объектов управления: учеб. пособие. / А.А. Иг­натьев, С.А. Игнатьев. - Саратов: СГТУ, 2008. - 44 с.

6. Теория вероятности и математическая статистика в примерах и зада­чах с применением EXCEL. / Г.В. Горелова, И.А. Кацко. - Ростов н/Д: Феникс, 2006.- 475 с.

СОДЕРЖАНИЕ

1. Лабораторная работа № 1 2

   1. Цель работы 2

   2. Основные понятия 2

   3. Порядок выполнения работы 6

   4. Пример выполнения работы 7

1.5. Содержание и оформление отчета 7

1.6. Варианты заданий 9

7. Вопросы для самоконтроля 10

8. Время, отведенное на выполнение работы 10

2. Лабораторная работа № 1 11

   1. Цель работы 11

   2. Основные понятия 11

   3. Порядок выполнения работы 13

2.4. Пример выполнения работы 15

2.5. Содержание и оформление отчета 16

2.7. Вопросы для самоконтроля 16

2.8. Время, отведенное на выполнение работы 16

2.9. Варианты заданий 18

ВАРИАНТЫ ЗАДАНИЙ

Вариант задания выбрать по номеру в журнале.