Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Построение одномерных моделей методом наименьших квадратов

Методические указания

к выполнению лабораторных работ

по курсу “Идентификация и диагностика систем”

для студентов специальности 210100

дневной, вечерней и заочной форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2009

Лабораторная работа № 1

Построение линейной одномерной модели методом наименьших квадратов

Цель работы - освоение алгоритма метода наименьших квадратов. Освоение основных приемов работы в электронных таблицах EXCEL.

ОСНОВНЫЕ ПОНЯТИЯ

При проведении исследований часто приходится отыскивать и изу­чать связи между различными процессами и их характеристиками.

Если некоторая величина однозначно связана с некоторой величи­ной , то такая связь называется функциональной .

На практике между двумя случайными величинами может существо­вать стохастическая связь, проявляющаяся в изменении закона распреде­ления этих величин, обнаруживать эту связь удается, как правило, только в результате многочисленных измерений и последующей статической обра­ботки полученных результатов.

Для установления вида зависимости, при стохастической связи вели­чины, т.е. для идентификации этой зависимости используется регрессион­ный анализ.

При этом различают положительную линейную и нелинейную, отри­цательную и неотрицательную регрессии.

Функция регрессии определяется в виде соответствующего матема­тического уравнения того или иного типа.

С помощью функции регрессии можно установить значение зависи­мой величины внутри интервала, заданные значения независимой пере­менной или же оценить в течение процесса внезапного интервала.

Под этой зависимостью понимают одностороннюю стохастическую связь.

(1)

Неизвестные параметры регрессии ивычисляются с помощью наименьших квадратов по уравнению:

(2)

Помимо простой линейной регрессии может использоваться мно­жественно линейная регрессия вида:

(3)

В этом случае, переменные оказывают соответственное влияние на зависимую переменную.

Задачами регрессионного анализа являются: установление формы за­висимости между переменными, оценка функций регрессии, оценка неиз­вестных значений зависимой переменной (прогноз).

Односторонняя зависимость случайной зависимой переменной Y от одной или нескольких независимых переменных X называется объясняю­щей регрессией. Такая зависимость может возникать тогда, когда при каж­дом фиксированном значении X, соответствующее значение Y подвержено случайному разбросу неконтролируемых факторов. Такая зависимость Y(X) называется регрессионной. Она может быть представлена в виде мо­дельного уравнения регрессии:

, (4)

где - случайная переменная, характеризующая отклонение от функции регрессии.

Линейный регрессионный анализ - это анализ, для которого функ­ция f(X) линейна относительно оцениваемых факторов.

Регрессионный анализ включает в себя две основные компоненты:

1. оценка вектора коэффициентов с помощью метода наименьших квадратов;

2. дисперсионный анализ – для оценки адекватности модели.

Для того чтобы провести регрессионный анализ необходимо:

• чтобы количество экспериментальных данных было больше либо равно 30 на один вход;

• распределение выходной величины должно быть нормальным;

• в процессе эксперимента дисперсия выходной величины Y не меня­ется: ;

• переменная X изменяется с пренебрежительно малыми ошиб­ками, то есть является детерминированной;

• выходные переменные X₁, X₂, … X_n стахостически независимы ме­жду собой: ;

• дискретность проведения экспериментов во времени берется та­ким образом, чтобы последовательно взятые значения Y₁, Y₂, Y₃ были стахостически независимыми, то есть больше времени затухания автокор­реляционной функции;

• учет динамики в регрессионном анализе производится в виде транспортного запаздывания, которое определяется как время нахождения максимума взаимно корреляционной функции X и Y.

На основании этих предпосылок получают уравнение регрессионной модели методом наименьших квадратов.

Алгоритм расчета уравнения линейной регрессии МНК

1. Проводим эксперимент, задаем не менее 30 значений X, , .

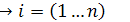2. Значения x_i и y_i и сводим их в таблицу в столбцы 2 и 3.

3. Находим квадрат входной величины .

4. Находим произведение входной и выходной величин .

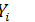5. Находим сумму входной и выходной величин .

6. Находим квадрат суммы входной и выходной величины .

7. Находим сумму входных величин .

8. Находим .

9. Находим сумму квадратов входных величин .

10. Находим сумму произведений входной и выходной величин .

11. Находим сумму входной и выходной величин

12. Находим сумму квадрата сумм и выходной величин

13. 

    (5)

    Находим коэффициенты b₀ и b₁ по формулам:

По формуле линейной регрессии находим расчетные значения вы­ходных величин: .

14. Находим отклонение расчетного значения от фактического значе­ния выходной величины: .

15. Находим квадрат отклонения: .

16. Находим сумму квадратов отклонений:

18. Рассчитываем 95% ошибку аппроксимации:

(6)

_,

_где - экспериментальное и расчетное значения выходной перемен­ной; N, m - соответственно, количество экспериментов и коэффициентов регрессионного уравнения (без учета b₀).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ

1. Подготовить в электронных таблицах EXCEL программу для реше­ния поставленной задачи:

Ввести наименование работы, фамилию студента, номер варианта работы. Подготовить таблицу, включающую:

• номера точек по порядку;

• значения входной переменной;

• значения выходной переменной;

• столбцы для промежуточных результатов вычислений;

• ввести формулы для расчета промежуточных переменных.

Внизу таблицы в двух ячейках ввести формулы для расчета коэффи­циентов уравнения (5).

В последних столбцах таблицы произвести расчет:

,

Рассчитать 95% ошибку аппроксимации

_,

_где - экспериментальное и расчетное значения выходной перемен­ной; N, m - соответственно, количество экспериментов и коэффициентов регрессионного уравнения (без учета b₀).

2. Построить графики зависимости экспериментальных и рассчитан­ных значений выходной переменной от входной переменной.

3. Провести анализ адекватности полученного уравнения.

4. Построить линию тренда и показать уравнение и R² на диаграмме.

5. Отформатировать все элементы таблицы и графики.

6. Скопировать исходные данные на второй лист вашей книги.

7. На 2 листе не пользуясь формулами для нахождения коэффициен­тов b0 и b1, подобрать их по критерий . Используйте команду Поиск решения.

8. Распечатать работу.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Задан линейный статический объект с 1 входом и 1 выходом.

Имеется выборка пассивного эксперимента объемом 21 точка, со­держащая значения входной и выходной переменных.

Период выборки обеспечивает отсутствие автокорреляции Х, Y.

Необходимо найти оценки коэффициентов регрессионного уравне­ния вида и оценку величины ошибки аппроксимации.

Пример лабораторной работы представлен на рисунке 1.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА

Отчет оформляется в текстовом редакторе Word на бумаге формата А4 ГОСТ 6656-76 (210х297 мм) и содержит:

1. Название лабораторной работы.

2. Цель работы.

3. Задание.

4. Результаты вычисления.

Рис. 1. Построение линейной модели методом наименьших квадратов

ВАРИАНТЫ ЗАДАНИЙ

Вариант задания выбрать по номеру в журнале.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Задачи регрессионного анализа.

2. Что называют объясняющей регрессией?

3. Какая зависимость называется регрессионной?

4. Предпосылки регрессионного анализа.

5. Вид модального уравнения регрессии.

6. Что такое линейный регрессионный анализ?

7. Компоненты регрессионного анализа.

8. Как рассчитываются коэффициенты одномерной линейной рег­рессионной модели.

9. Как рассчитать 95% ошибку аппроксимации.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

Подготовка к работе – 0,5 акад. часа.

Выполнение работы – 0,5 акад. часа.

Расчеты на ЭВМ – 0,5 акад. часа.

Оформление работы – 0,5 акад. часа.

ЛитЕратура

1. Идентификация объектов управления: учеб. пособие. / А. Д. Семенов, Д. В. Арта­монов, А. В. Брюхачев. - Пенза: ПГУ, 2005. - 211 с.

2. Основы теории идентификации объектов управления: учеб. пособие. / А.А. Иг­натьев, С.А. Игнатьев. - Саратов: СГТУ, 2008. - 44 с.

3. Теория вероятности и математическая статистика в примерах и зада­чах с применением EXCEL. / Г.В. Горелова, И.А. Кацко. - Ростов н/Д: Феникс, 2006.- 475 с.

Лабораторная работа № 2