Оценка значимости коэффициентов регрессии

Для проверки значимости анализируется отношение коэффициента регрессии и его среднеквадратичного отклонения. Это отношение является распределением Стьюдента, то есть для определения значимости используем t – критерий:

(7)

где ;

- СКО от остаточной дисперсии;

- сумма отклонений от среднего значения

Если t_рас.>t_таб., то коэффициент b_i является значимым.

Доверительный интервал определяется по формуле:

, (8)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Взять исходные данные согласно варианту работы (по номеру студента в журнале). Задан статический объект управления с двумя входами X₁, X₂ и одним выходом Y. На объекте проведен пассивный эксперимент и получена выборка объемом 30 точек, содержащая значения Х₁, Х₂ и Y для каждого эксперимента.

2. Открыть новый файл в Excel 2007. Ввести исходную информацию в столбцы исходной таблицы - значения входных переменных X₁, Х₂ и выходной переменной Y.

3. Подготовить дополнительно два столбца для ввода расчетных значений Y и остатков.

4. Вызвать программу «Регрессия»: Данные/ Анализ данных/ Регрессия.

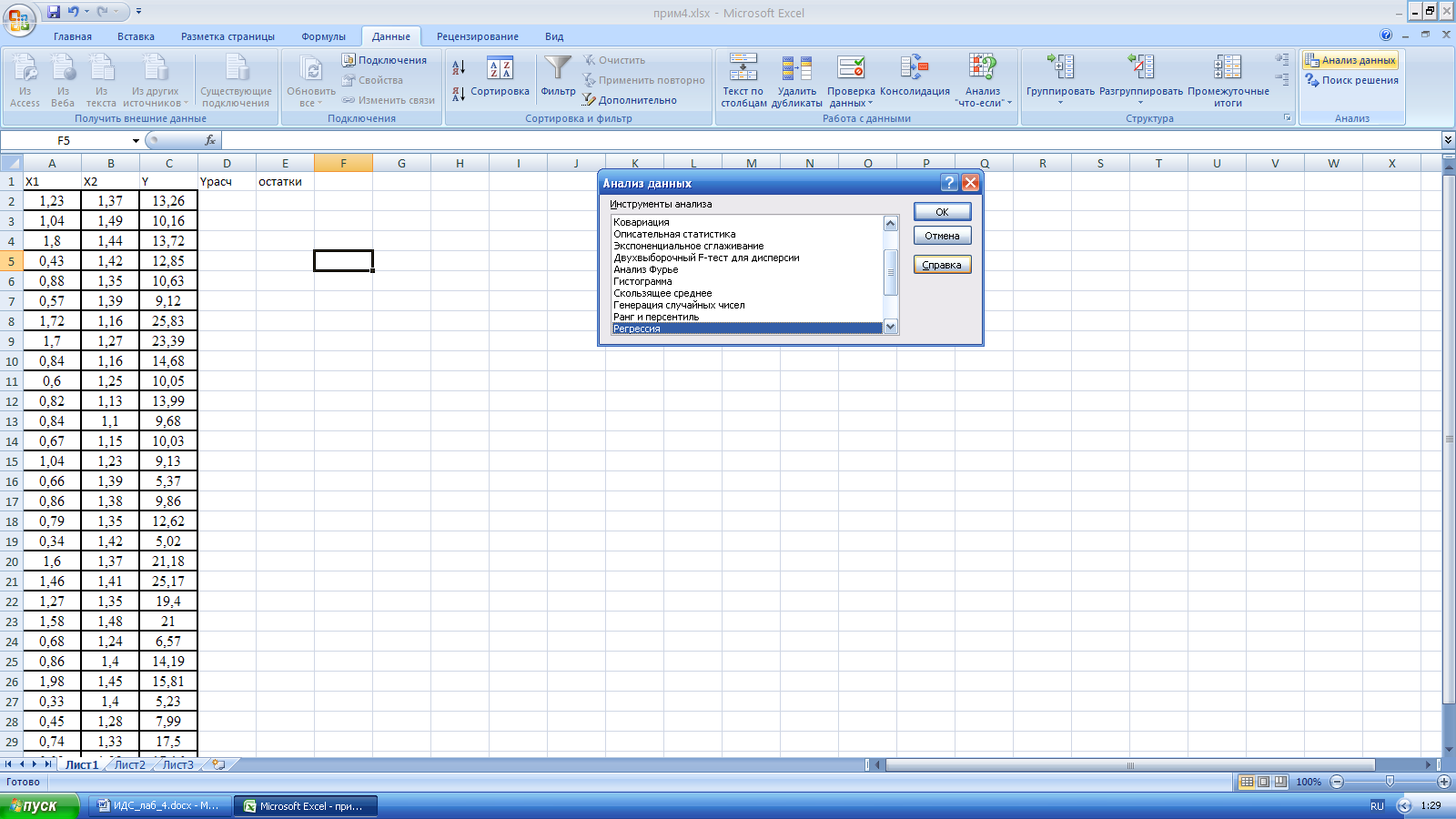
Рис. 1. Диалоговое окно «Анализ данных».

5. Ввести в диалоговое окно «Регрессия» адреса исходных данных:

• входной интервал Y, входной интервал X (2 столбца),

• установить уровень надежности 95%,

• в опции «Выходной интервал, указать левую верхнюю ячейку места вывода данных регрессионного анализа (первую ячейку на 2-странице рабочего листа),

• включить опции «Остатки» и «График остатков»,

• нажать кнопку ОК для запуска регрессионного анализа.

Рис. 2. Диалоговое окно «Регрессия».

6. Excel выведет 4 таблицы и 2 графика зависимости остатков от переменных Х1 и Х2.

7. Отформатировать таблицу «Вывод итогов» - расширить столбец с наименованиями выходных данных, сделать во втором столбце 3 значащие цифры после запятой.

8. Отформатировать таблицу «Дисперсионный анализ»- сделать удобным для чтения и понимания количество значащих цифр после запятых, сократить наименование переменных и настроить ширину столбцов.

9. Отформатировать таблицу коэффициентов уравнения - сократить наименование переменных и скорректировать при необходимости ширину столбцов, сделать удобным для чтения и понимания количество значащих цифр, удалить 2 последних столбца (значения и разметку таблицы).

10. Данные из таблицы «Вывод остатка» перенести в подготовленные столбцы исходной таблицы, затем таблицу «Вывод остатка» удалить (опция «специальная вставка»).

11. Ввести полученные оценки коэффициентов в исходную таблицу.

12. Подтянуть таблицы результатов по максимуму вверх страницы.

13. Построить под таблицами диаграммы Yэксп, Yрасч и ошибки прогноза (остатка).

14. Отформатировать диаграммы остатков. По полученным графикам оценить правильность модели по входам Х1, Х2.

15. Распечатать результаты регрессионного анализа.

16. Разобраться с результатами регрессионного анализа.

17. По промежуточным результатам рассчитать коэффициент множественной корреляции, расчетные значения t-критериев, доверительные интервалы, остаточную ошибку модели .

18. Подготовить отчет по работе.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Прием выполнения регрессионного анализа в пакете EXCEL представлен на рисунках 3-5.

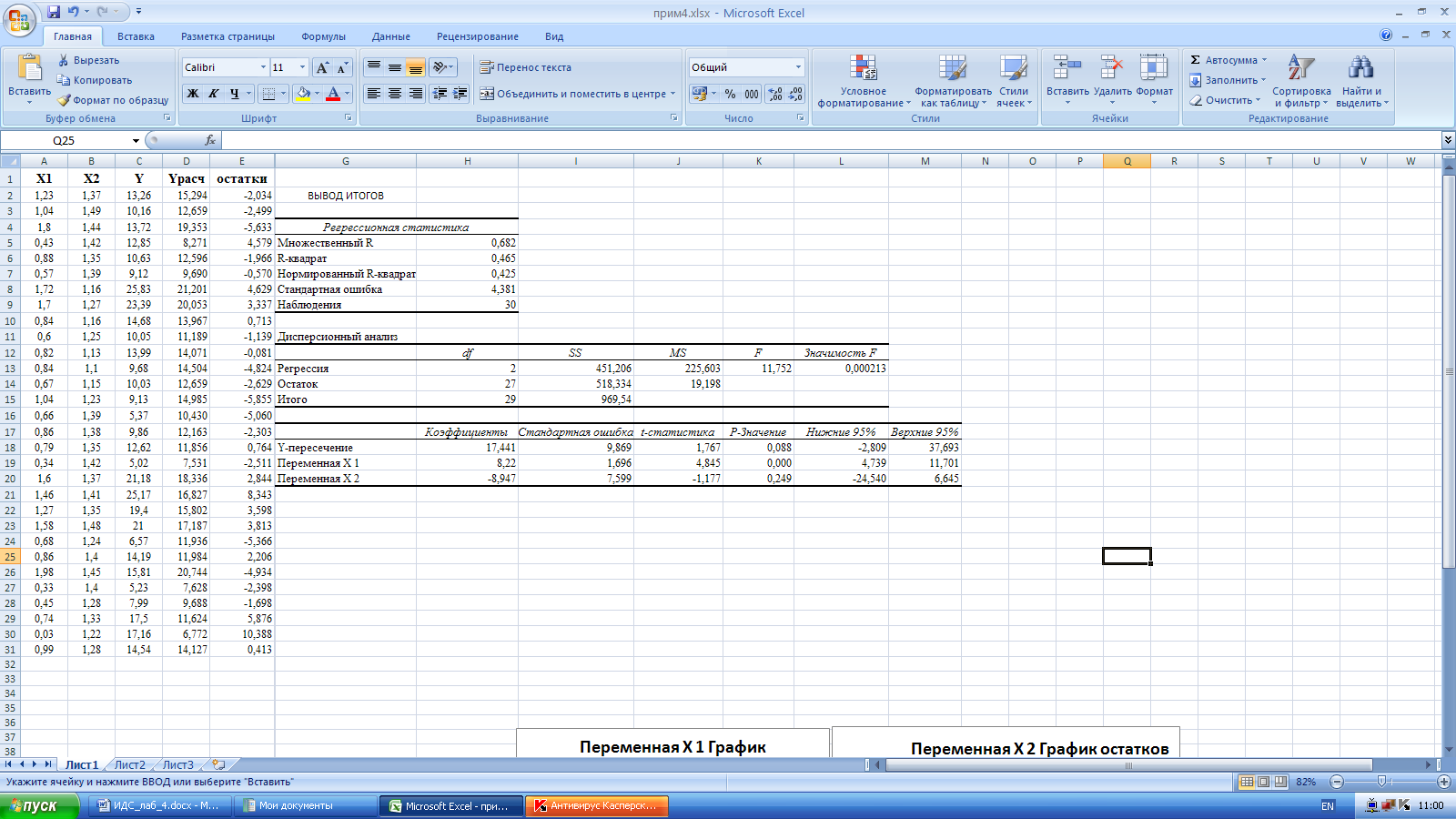
Рис. 3. Пример регрессионного анализа в пакете EXCEL.

Рис.4 . Графики остатков переменных Х1, Х2

Рис. 5. Графики Yэксп,Yрасчи ошибки прогноза (остатка).

.

По данным регрессионного анализа можно сказать:

1. Уравнение регрессии полученное с помощью Excel, имеет вид:

2. Коэффициент детерминации:

Вариация результата на 46,5% объясняется вариацией факторов.

2. Общий F-критерий проверяет гипотезу о статистической значимости уравнения регрессии. Анализ выполняется при сравнении фактического и табличного значения F-критерия Фишера.

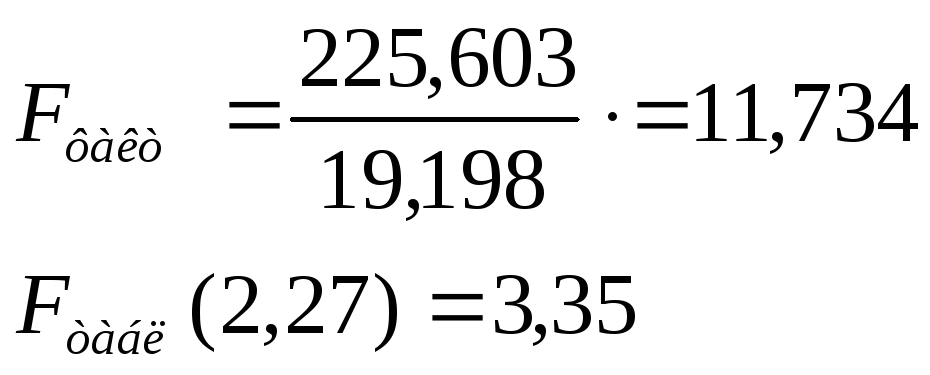
Так как фактическое значение превышает табличное , то делаем вывод, что полученной уравнение регрессии статистически значимо.

2. Коэффициент множественной корреляции:

2. Определяем доверительный интервал для коэффициента b₀:

t_таб.(29, 0.975)=2.05

Проверка значимости коэффициента b₀:

Доверительный интервал:

2. Определяем доверительный интервал для коэффициента b₁:

Проверка значимости коэффициента b₁:

t_рас.>t_таб., коэффициент b₁ является значимым

Доверительный интервал:

2. Определяем доверительный интервал для коэффициентаb₂:

Проверка значимости для коэффициентаb₂:

Определяем доверительный интервал:

ВАРИАНТЫ ЗАДАНИЙ

Таблица 2. Варианты заданий

№ варианта

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Результативный признак Yi

Y1

Y1

Y1

Y1

Y1

Y1

Y1

Y1

Y1

Y1

Y2

Y2

Y2

Y2

Y2

№ фактора Xi

X1

X1

X1

X1

X2

X2

X2

X3

X3

X4

X1

X1

X1

X1

X2

№ фактора Xi

X2

X3

X4

X5

X3

X4

X5

X4

X4

X5

X2

X3

X4

X5

X3

Продолжение таблицы 1

№ варианта

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

Результативный признак Yi

Y2

Y2

Y2

Y2

Y2

Y3

Y3

Y3

Y3

Y3

Y3

Y3

Y3

Y3

Y3

№ фактора Xi

X2

X2

X3

X3

X4

X1

X1

X1

X1

X2

X2

X2

X3

X3

X4

№ фактора Xi

X4

X5

X4

X4

X5

X2

X3

X4

X5

X3

X4

X5

X4

X4

X5

Таблица 3. Исходные данные

№	Y1	Y2	Y3	X1	X2	X3	X4	X5
1	9,26	204,2	13,26	0,23	0,78	0,4	1,37	1,23
2	9,36	209,6	10,16	0,24	0.75	0,26	1,49	1,04
3	12,11	222,6	13,72	0,19	0,68	0,4	1,44	1,8
4	10,81	236,7	12,85	0,17	0,7	0,5	1,42	0,43
5	9,35	62,0	10,63	0,23	0,62	0,4	1,35	0,88
6	9,87	53,1	9,12	0,43	0,76	0,19	1,39	0,57
7	8,17	172,1	25,83	0,31	0,73	0,25	1,16	1,72
8	9,12	56,5	23,39	0.26	0,71	0,44	1,27	1,7
9	5,88	52,6	14,68	0,49	0,69	0,17	1,16	0,84
10	6,3	46,6	10,05	0,36	0,73	0,39	1,25	0,6
11	6,22	53,2	13,99	0,37	0,68	0,33	1,13	0,82
12	5,49	30,1	9,68	0,43	0,74	0,25	1,1	0,84
13	6,5	146,4	10,03	0,35	0,66	0,32	1,15	0,67
14	6,61	18,1	9,13	0,38	0,72	0,02	1,23	1,04
15	4,32	13,6	5,37	0,42	0,68	0,06	1,39	0,66
16	7,37	89,9	9,86	0,3	0,77	0,15	1,38	0,86
17	7,02	62,5	12,62	0,32	0,78	0,08	1,35	0,79
18	8,25	46,3	5,02	0,25	0,78	0,2	1,42	0,34
19	8,15	103,5	21,18	0,31	0,81	0,2	1,37	1,6
20	8,72	73,3	25,17	0,26	0,79	0,3	1,41	1,46
21	6,64	76,6	19,4	0,37	0,77	0,24	1,35	1,27
22	8,1	73,3	21	0,29	0,78	0,1	1,48	1,58
23	5,52	32,3	6,57	0,34	0,72	0,11	1,24	0,68
24	9,37	199,6	14,19	0,23	0,79	0,47	1,4	0,86
25	13,17	596,1	15,81	0,17	0,77	0,53	1,45	1,98
26	6,67	71,2	5,23	0,29	0,8	0,34	1,4	0,33
27	5,68	90,8	7,99	0,41	0,71	0,2	1,28	0,45
28	5,22	82,1	17,5	0,41	0,79	0,24	1,33	0,74
29	10,02	76,2	17,16	0,22	0,76	0,54	1,22	0,03
30	8,16	119,5	14,54	0,29	0,78	0,4	1,28	0,99

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Задачи регрессионного анализа.

2. Предпосылки регрессионного анализа.

3. Основное уравнение дисперсионного анализа.

4. Что показывает F- отношение Фишера?

5. Как определяется табличное значение критерия Фишера?

6. Что показывает коэффициент детерминации?

7. Как определить значимость коэффициентов регрессии?

8. Как определить доверительный интервал коэффициентов регрессии?

9. Как определить расчетные значение t-критерия?

10. Как определить табличное значение t-критерия?

11. Сформулируйте основную идею дисперсионного анализа, для решения каких задач он наиболее эффективен?

12. Каковы основные теоретические предпосылки дисперсионный анализ?

13. Произведите разложение общей суммы квадратов отклонений на составляющие в дисперсионном анализе.

14. Как получить оценки дисперсий из сумм квадратов отклонений?

15. Как получаются необходимые числа степеней свободы?

16. Как определяется стандартная ошибка?

17. Поясните схему двухфакторного дисперсионного анализа.

18. Чем отличается перекрестная классификация от иерархической классификации?

19. Чем отличаются сбалансированные данные?

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА

Отчет оформляется в текстовом редакторе Word на бумаге формата А4 ГОСТ 6656-76 (210х297 мм) и содержит:

1. Название лабораторной работы.

2. Цель работы.

3. Задание.

4. Результаты вычисления.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ

ЛАБОРАТОРНОЙ РАБОТЫ

Подготовка к работе – 0,5 акад. часа.

Выполнение работы – 0,5 акад. часа.

Расчеты на ЭВМ – 0,5 акад. часа.

Оформление работы – 0,5 акад. часа.

ЛитЕратура

1. Идентификация объектов управления. / А. Д. Семенов, Д. В. Артамонов, А. В. Брюхачев. Учебное пособие. - Пенза: ПГУ, 2003. - 211 с.

2. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTIC и EXCEL. / Вуколов Э.А. Учебное пособие. - М.: ФОРУМ, 2008. - 464 с.

3. Основы теории идентификации объектов управления. / А.А. Игнатьев, С.А. Игнатьев. Учебное пособие. - Саратов: СГТУ, 2008. - 44 с.

4. Теория вероятности и математическая статистика в примерах и задачах с применением EXCEL. / Г.В. Горелова, И.А. Кацко. - Ростов н/Д: Феникс, 2006.- 475 с.

СОДЕРЖАНИЕ

1. Цель работы 2

2. Основные понятия 2

3. Порядок выполнения работы 6

4. Пример выполнения работы 9

5. Вопросы для самоконтроля 13

6. Содержание и оформление отчета 14

7. Время, отведенное на выполнение работы 14

8. Литература 14