методические указания по лабораторной работе / ИДС_лаб_1 АНАЛИЗ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

АНАЛИЗ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

Методические указания к выполнению лабораторной работы

по курсу “Идентификация и диагностика систем”

для студентов специальности 210100

дневной и вечерней форм обучения

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

Балаково 2009

Цель работы - освоение методов и приобретение навыков исследования случайных сигналов систем управления, закрепление методов работы в электронных таблицах Excel.

ОСНОВНЫЕ ПОНЯТИЯ

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений.

Случайные величины бывают дискретные и непрерывные.

Случайная величина называется дискретной, если множество ее значений конечно или бесконечно, но счетно, то есть элементы можно пронумеровать натуральными числами.

Случайная величина называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема во всех случаях, кроме точек излома.

Случайные величины обладают определенными закономерностями и параметрами, зная которые можно построить технологический процесс или систему управления, к ним относятся:

• математическое ожидание М(х);

• дисперсия D(x);

• функция распределения F(x);

• плотность распределения для непрерывных величин

• корреляционная функция R_xx(x);

• спектральная плотность

Математическое ожидание – это наиболее вероятное значение случайной величины. Для непрерывной случайной величины математическое ожидание определяется:

(1)

Дисперсией D(x) случайной величины называется математическое ожидание квадрата ее отклонений от математического ожидания случайной величины:

(2)

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого текущего х вероятность того, что случайная величина Х примет значение меньше текущего значения х:

(3)

Вероятность события – отношение количества событий, благоприятствующих случайной величине к общему количеству выпадений.

Плотностью распределения непрерывной случайной величины называется производная ее функции распределения:

(4)

Она существует только для непрерывных случайных величин.

График плотности вероятности называется кривой распределения.

Существуют различные законы распределения как для дискретных величин, так и для непрерывных случайных величин.

Основные законы распределения непрерывных случайных величин.

1. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a,b], если ее плотность вероятности постоянна на том отрезке и равна нулю вне того отрезка, т.е.:

(5) Функция распределения случайной величины X по равномерному закону, есть

(6)

ее математическое ожидание

, (7)

а дисперсия

(8)

2. Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса), если ее плотность вероятности с параметрами a и имеет вид:

(9)

Кривую по нормальному закону распределения называют кривой Гаусса. Она имеет максимум в точке a с ординатой:

(10)

и две точки перегиба с ординатами:

(11)

Кривая симметрична относительно прямой x=a. Математическое ожидание случайной величины X, распределенной по нормальному закону, равно параметру а этого закона:

M(x)=а, (12)

а ее диспепсия (13)

Функция распределения выражается в виде:

(14)

3. Непрерывная случайная величина X имеет показательный закон распределения (экспоненциальный) с параметром λ > 0, если плотность вероятности имеет вид:

, (15)

Функция распределения показательного закона распределения

, (16)

Математическое ожидание

, (17)

Диспепсия

. (18)

4. Непрерывная случайная величина X имеет логарифмически-нормальный закон распределения (логонормальный), если ее логарифм подчинен нормальному закону, его плотность вероятности имеет вид:

, (19)

Функция распределения:

(20)

Математическое ожидание

(21)

Диспепсия

(22)

где - среднее значение входной величины.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ

В разделах 1-6 производится подготовка таблицы и генерация случайных процессов.

1. В электронных таблицах Excel  2007 готовится таблица 1 для генерации четырех различных случайных процессов.

Таблица 1

Лабораторная работа 1			Анализ характеристик случайных процессов
Группа. ФИО.				Заданные параметры
				a
				b
				R	0,8
	Равномерное распределение	Нормальное распределение		Нормальное распределение	Нормальное распределение
№п/п	R(0.5,1/12)	N(0,1,0)		Белый шум N(a,b,0)	Цветной (a,b,R1)

2. В первый столбец (ячейки А8:А108) заносятся номера строк по порядку (от 0 до 100).

3. Во втором столбце генерируется случайный процесс с равномерным распределением в диапазоне 0-1. Такой процесс обозначается R(0.5, 1/12), где R означает равномерное распределение; 0.5 – среднее значение;1/12 – среднеквадратическое значение равномерного случайного процесса в диапазоне 0–1.

Генерация производится путем использования встроенных функций Excel раздела «Анализ данных»:

Данные/Анализ данных/Генерация случайных чисел/Диалоговое окно «Генерация случайных чисел», в котором вводятся данные:

• Число (количество) переменных – 1.

• Число случайных чисел (объем выборки) – 101.

• Распределение – равномерное в диапазоне от 0 до 1.

• Выходной интервал – указываются координаты столбца 2 таблицы.

• Далее нажимается «ОК»

Во втором столбце выводится случайный процесс с заданными параметрами.

4. В третьем столбце генерируется нормальный случайный процесс N(a,b,R), где , соответственно, среднее, среднее квадратичное отклонение и первая ордината автокорреляционной функции случайного процесса.

В диалоговом окне «Генерация случайных чисел» вводятся данные:

• Число переменных – 1.

• Число случайных чисел – 101.

• Распределение – нормальное, среднее значение 0, стандартное отклонение 1.

• Выходной интервал – указываются координаты столбца 3 подготовленной таблицы.

• Далее нажимается «ОК»

В третьем столбце выводится случайный процесс с заданными параметрами.

5. В четверном столбце аналогично генерируется нормальный случайный процесс, где ; - количество букв в фамилии и имени студента.

Необходимо понять, как изменился уровень и диапазон колебания случайного процесса.

6. В пятом столбце рассчитывается случайный процесс, полученный путем пропускания случайного процесса N(a,b,R) через апериодическое звено первого порядка. При этом выходной сигнал рассчитывается по рекуррентному разностному уравнению:

здесь R – параметр фильтра, на первом этапе выбираемый равным 0,8.

Затем, задавая значения _, изучить изменение графика выходного сигнала фильтра (изменение среднего, дисперсии).

7. Для каждого случайного процесса постройте график и отформатируйте по примеру, приведенному на рис.1. Графики 3 и 4 постройте вместе.

8. Расчет и построение графиков дифференциальной и интегральной функций распределения для всех сгенерированных случайных процессов. Для расчета и построения графиков гистограмм используются встроенные функции Excel раздела «Анализ данных»:

Данные/Анализ данных/Гистограмма /Диалоговое окно «Гистограмма:

В диалоговом окне «Гистограмма» вводятся данные:

Входной интервал – указывается диапазон ячеек таблицы исследуемого случайного процесса.

Интервал карманов (диапазоны изменения случайной величины при построении гистограммы). Рядом с таблицей (через один столбец) укажите границы диапазонов. Для этого по графику случайного процесса оцените максимальное и минимальное значения и весь диапазон разбейте на 8-16 диапазонов. Границы выбираются удобные для анализа. (Excel по умолчанию сам может назначить границы, но они получаются дробные и не очень удобные для анализа).

Пример указания карманов для случайного процесса с равномерным распределением:

• В ячейке G1 напишите слово «Карманы».

• По графику случайного процесса определите минимальное и максимальное значения (например, 0 и 1).

• Разбейте диапазон, например на 10 диапазонов, т.е. введите в блок ячеек G2:G12 числа от 0 до 1 с шагом 0,1.

Параметры вывода:

Выходной интервал – указывается адрес одной ячейки, начиная с которой Excel выводит таблицу и графики функций распределения. Указывается ячейка справа от шапки введенных карманов.

Ставятся флажки вывода интегральной функции – интегральный процент и вывод графика.

9. Проводится форматирование таблиц и графиков.

   1. Для обеспечения удобства чтения таблиц и их размещения на одной странице: настроить ширину столбцов, сделать количество значащих цифр не более 4-х (2-3 знака после запятой), оформить рамки для ячеек и столбцов таблицы.

   2. Форматирование графика:

• Расположить графики под или рядом с таблицами в пределах границ страницы.

• Ввести название диаграмм, осей графиков и др.

• Выбрать удобные для восприятия цвета, толщину линий, размер точек графика.

• Сделать надписи графика шрифтами с номерами 6-10.

• Расположить все надписи графика в места, обеспечивающие наглядность.

Используя команду «Предварительный просмотр» убедиться, что таблицы и графики находятся на одной странице и обеспечиваются их наглядность.

Проводится анализ полученных результатов и подготовка выводов.

ПРИМЕР ЛАБОРАТОРНОЙ РАБОТЫ

Пример лабораторной работы представлен на рисунке 1.

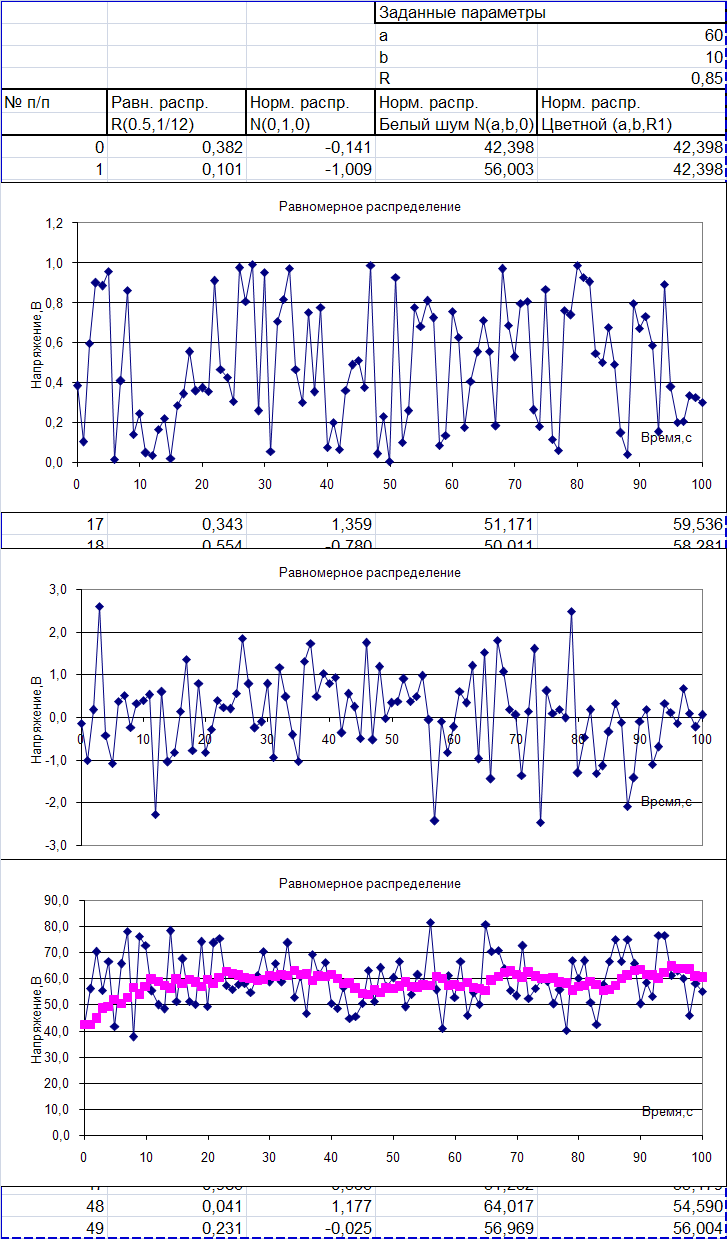
Рис. 1. Генерация случайных процессов

Гистограммы процессов равномерного, нормального распределения и нормального распределения полученного путем пропускания случайного процесса через апериодическое звено первого порядка представлены на рисунках 2-4.

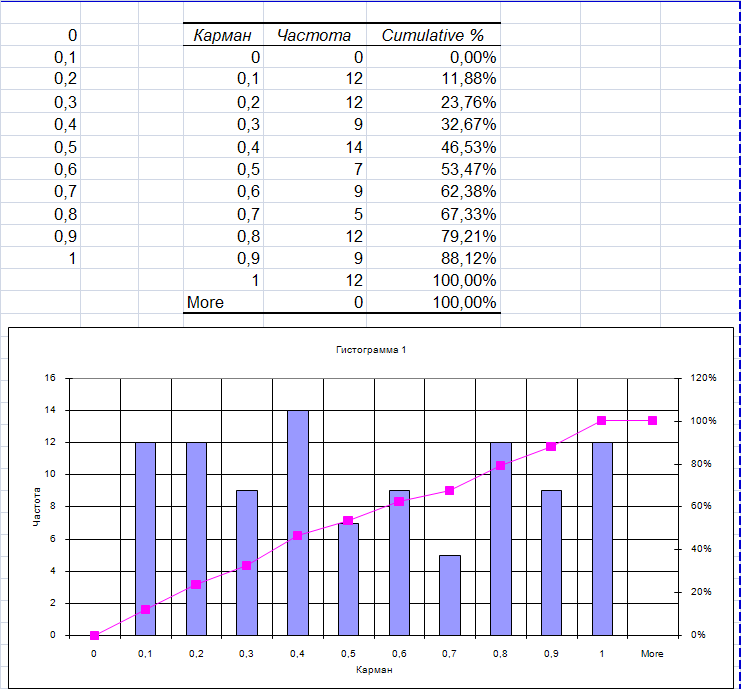
Рис. 2. Гистограмма процесса равномерного распределения

Рис. 3. Гистограмма процесса нормального распределения

Р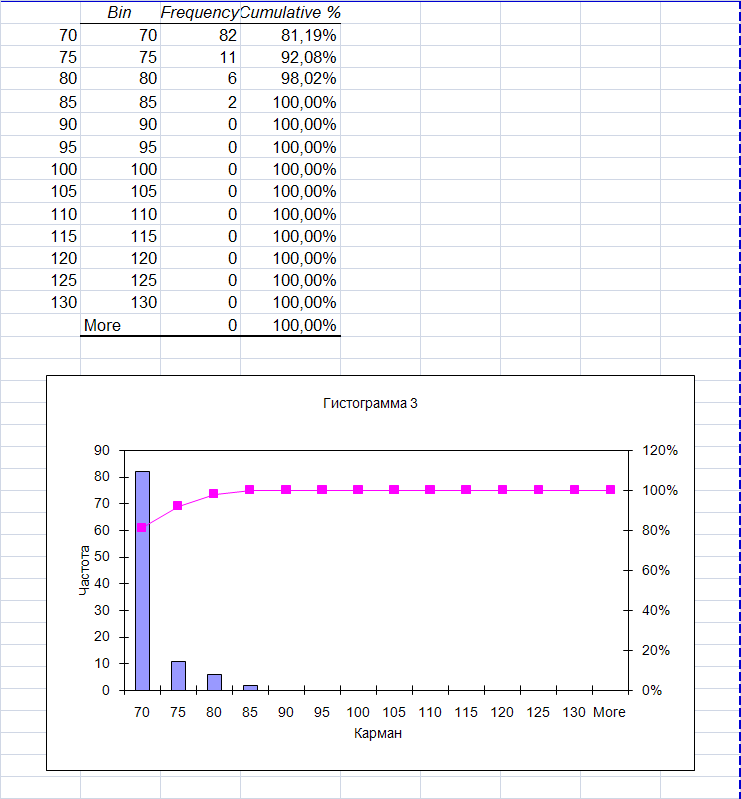 ис. 4. Гистограмма процесса нормального распределения, полученного путем пропускания случайного процесса через апериодическое звено первого порядка

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Основные характеристики случайной величины.

2. Понятие математического ожидания случайной величины.

3. Понятие дисперсии случайной величины.

4. Понятие функции распределения случайной величины.

5. Понятие плотности распределения для непрерывных величин случайной величины.

6. Основные законы распределения непрерывной случайной величины.

7. Равномерный закон распределения непрерывной случайной величины.

8. Нормальный закон распределения непрерывной случайной величины.

9. Показательный закон распределения непрерывной случайной величины.

10. Логарифмический нормальный закон распределения непрерывной случайной величины.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА

Отчет оформляется в текстовом редакторе Word на бумаге формата А4 ГОСТ 6656-76 (210х297 мм) и содержит:

1. Название лабораторной работы.

2. Цель работы.

3. Задание.

4. Результаты вычисления.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ

ЛАБОРАТОРНОЙ РАБОТЫ

Подготовка к работе – 0,5 акад. часа.

Выполнение работы – 0,5 акад. часа.

Расчеты на ЭВМ – 0,5 акад. часа.

Оформление работы – 0,5 акад. часа.

ЛитЕратура

1. Идентификация объектов управления. / А. Д. Семенов, Д. В. Артамонов, А. В. Брюхачев. Учебное пособие. - Пенза: ПГУ, 2003. - 211 с.

2. Основы теории идентификации объектов управления. / А.А. Игнатьев, С.А. Игнатьев. Учебное пособие. - Саратов: СГТУ, 2008. - 44 с.

3. Теория вероятности и математическая статистика в примерах и задачах с применением EXCEL. / Г.В. Горелова, И.А. Кацко. Ростов н/Д: Феникс, 2006.- 475 с.

СОДЕРЖАНИЕ

1. Цель работы 2

2. Основные понятия 2

3. Порядок выполнения работы 5

4. Пример выполнения работы 9

5. Вопросы для самоконтроля 12

6. Содержание и оформление отчета 12

7. Время, отведенное на выполнение работы 13

8. Литература 13

АНАЛИЗ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

Методические указания к выполнению лабораторной работы

по курсу “Идентификация и диагностика систем”

для студентов специальности 210100

дневной и вечерней форм обучения

Составил: Стельмах Ирина Валентиновна

Рецензент Т.Н. Скоробогатова

Редактор Л.В.Максимова

Подписано в печать Формат 60х84 1/16

Бумага тип Усл. печ. л. Уч. – изд.л.

Тираж 100 экз. Заказ Бесплатно

Саратовский государственный технический университет

410054, г. Саратов, ул. Политехническая, 77

Копипринтер БИТТиУ, 413840, г. Балаково, ул. Чапаева, 140

17