Свойства логических операций.

1. ( А) ⇔ (А).	7. ((А∧В)∧C) ⇔ (А∧(В ∧С)).
2. ( (А∨B)) ⇔ ( А∧B).	8. ((А∨В)∧C) ⇔ ((А∧C)∨(В ∧С)).
3. ( (А∧B)) ⇔ ( А∨B).	9. ((А∧В)∨C) ⇔ ((А∨C)∧ (В∧С)).
4. (А∨B) ⇔ (B∨A).	10. (А ⇒ В) ⇔ ( А∨В).
5. (А∧B) ⇔ (B∧A).	11. (А ⇒ B) ⇔ ( B ⇒ A).
6. ((А∨В)∨C) ⇔ (А∨(В ∨С)).	12. (А⇔В) ⇔ (A⇒B)∧(B⇒A).

        Док-во. Для доказательства любой из приведённых формул требуется построить таблицы истинности для частей формулы, стоящих слева и справа от символа эквивалентности ⇔, для всех значений истинности входящих в формулу высказываний, и показать, что они совпадают. Докажем, например, формулу 8. Таблица истинности:

А	В	С	А ∨B		(А∨В)∧С		А ∧С	В ∧C		(А ∧С)∨(В∧С)
0	0	0	0		0		0	0		0
0	0	1	0		0		0	0		0
0	1	0	1		0		0	0		0
0	1	1	1		1		0	1		1
1	0	0	1		0		0	0		0
1	0	1	1		1		1	0		1
1	1	0	1		0		0	0		0
1	1	1	1		1		1	1		1

        Значения истинности для левой и правой частей формулы совпадают при любых истинностях входных высказываний, следовательно, левая и правая части формулы действительно эквивалентны. (Отметим аналогию между этой формулой и формулой 10. A∩(B∪C) = (A∩B)∪(A∩C) из раздела "1. Элементы терии множеств.").         В дальнейшем мы будем отождествлять высказывание и его значение истинности, т.е. считать, что А = 1, если А - истинно, и А = 0, если А - ложно.

2. Элементы математической логики.

2.2. Кванторы.

        В этом разделе мы расширим понятие термина "высказывание", чтобы ввести в рассмотрение утверждения вида х > 7. Строго говоря, это утверждение не является высказыванием в смысле опр.2.1.1., так как мы не можем сказать, истинно оно или ложно (оно истинно, если, например, x∈[12,15] и ложно, если x∈[ 2, 5]). Тем не менее, утверждения, содержащие переменные x, y, z,… с областями возможных значений X, Y, Z,…, обладающие тем свойством, что для каждого набора переменных x∈X, y∈Y, z∈Z,… истинность утверждения может быть установлена, в дальнейшем тоже будем называть высказываниями. Зависимость высказываний A, В, ... от переменной x будем обозначать как А(х), В(х),… x∈X. Подмножество Х(А)⊆Х множества Х такое, что для любого х∈Х(А) высказывание А(х) истинно, будем называть областью истинности высказывания А (так, для высказывания х>-2, X = [-5, 5] будет Х(А) = (-2, 5]).

        Кванторы - логические операции, с помощью которых по некоторому высказыванию А(х) получают новые высказывания, характеризующие область истинности высказывания А(х).

        Опр. 2.2.1. Квантором всеобщности (обозначение - ∀) высказывания А(х), x∈X, называется логическая операция, имеющая значение "истина", если высказывание А(х) истинно для любого элемента x∈X, и значение "ложь" в противоположном случае (т.е. в случае, когда хотя бы для одного x∈X высказывание А(х) ложно).         Формула x∈X, А(х) читается как "для любого х, принадлежащего Х, справедливо А(х)"; "все х из Х удовлетворяют условию А(х)" и т.д. Формальное определение квантора всеобщности:                  Примеры: высказывание ("∀х ∈ [-2,4], x² > -2) - истинно, высказывание ("∀х ∈ [-2,4], x² > 16) - ложно, высказывание ("∀х ∈ N, x² > 0) - истинно, высказывание ("∀х ∈ R, x² > 0) - ложно.

        Опр. 2.2.2. Квантором существования (обозначение - ∃) высказывания А(х), x ∈ X, называется логическая операция, имеющая значение "истина", если высказывание А(х) истинно хотя бы для одного элемента x ∈ X, и значение "ложь" в противоположном случае (т.е. в случае, когда высказывание А(х) ложно для всех x ∈ X).         Формула ∃х∈Х, А(х) читается как "существует ( найдётся) (хотя бы один) элемент х, принадлежащий Х, для которого справедливо А(х)". Формальное определение квантора существования:                  Примеры: высказывание (∃ х ∈ [-2,4], x² > 20) - ложно, высказывание (∃ х ∈ [-2,4], x² > 10) - истинно, высказывание (∃ х ∈ N, x² = 0) - ложно, высказывание (∃ х ∈ R, x² = 0) - истинно.

        Опр. 2.2.3. Квантором существования и единственности (обозначение -∃!) высказывания А(х), x ∈ X, называется логическая операция, имеющая значение "истина", если на множестве X существует элемент x, для которого высказывание А(х) истинно, и такой элемент единственен, и значение "ложь" в противоположном случае (т.е. в случае, когда высказывание А(х) ложно для любого элемента x ∈ X либо А(х) истинно более чем для одного элемента x ∈ X.         Формула ∃! х ∈ Х, А(х) читается как "существует единственный элемент х, принадлежащий Х, для которого справедливо А(х)". Формальное определение квантора существования и единственности: 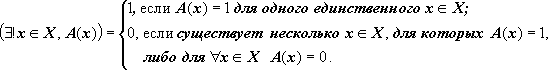                 Примеры: высказывание (∃! x ∈ [-2,4], x² ≥ 16 ) - истинно, высказывание (∃! x ∈ [-2,4], x² > 15 ) - ложно, высказывание (∃! x ∈ N, x² ≤ 1) - истинно, высказывание (∃! x ∈ R, x² ≤ 1) - ложно.

        Применение кванторов позволяет компактно записывать формулировки теорем, определений и других математических утверждений. Например, теорема о существовании корней квадратного уравнения запишется так:          ∀a ∈ R, ∀b ∈ R, ∀c ∈ R, a ≠ 0 (∃x ∈ R   (ax² + bx + c = 0) ⇔ b² - 4ac ≥ 0)

        При проведении математических рассуждений (доказательство теорем от противного, формулировки противоположных теорем и т.д.) часто приходится строить отрицания некоторых утверждений. Рассмотрим простой пример. Пусть дано определение: "Группа называется хорошей, если любой (∀)студент этой группы - хороший", требуется построить логически следующее из этого определения новое - определение плохой группы. Правильный ответ: "Группа называется плохой, если хотя бы один (∃)студент этой группы - плохой". Этот пример подсказывает следующие правила взаимодействия кванторов существования и единственности с операцией отрицания:         (∀x ∈ X, A(x)) ⇔ ∃x ∈ X, A(x);         (∃x ∈ X, A(x)) ⇔ ∀x ∈ X, A(x).         Док-во. Докажем первую эквивалентность. Если истинно высказывание (∀x ∈ X, A(x)) (не для ∀х ∈ Х истинно А(х)), то ∃х ∈ Х, для которого А(х) ложно, т.е. истинно А(х). Импликация (∀x ∈ X, A(x)) ⇒ ∃x ∈ X, A(x) доказана. Если истинно высказывание ∃x ∈ X, A(x) (существует х ∈ Х, для которого А(х) ложно), то не для любого х ∈ Х истинно А(х), т.е. (∀x ∈ X, A(x)). Импликация ∃x ∈ X, A(x) ⇒ (∀x ∈ X, A(x)) доказана. По формуле 12 таблицы Свойства логических операций из доказанных импликаций следует эквивалентность левой и правой частей первой формулы.         Аналогично доказывается вторая формула. Фор-мулы 1 и 2 имеют простой смысл. Именно, если мы хотим опровергнуть утверждение ∀х ∈ Х, А(х) (для любого х из Х верно А(х)), достаточно найти хотя бы один х, для которого А(х) неверно: ∃х ∈ Х, А(х). Если опровергается утверждение ∃х ∈ Х, А(х) "существует х, для которого верно А(х)", необходимо доказать, что А(х) неверно для любого х: ∀х ∈ Х, А(х).

        Задание. Самостоятельно доказать формулу 2.

        Если высказывание А(х) содержит несколько кванторов, то операция отрицания меняет каждый из них. Так, отрицание утверждения "число b есть предел функции f(x) в точке x = a…."          запишется так:         .