3.4. Границы числовых множест.
Пусть
Х
= {x|
x
∈
R}
- некоторое подмножество множества
действительных чисел.
Определения.
3.4.1.
Если существует число М
∈
R
такое, что для ∀х
∋
Х
выполняется неравенство х
< М,
то множество Х
называется ограниченным сверху (числом
М).
Число М
называется верхней границей множества
Х.
3.4.2.
Если существует число m
∈
R
такое, что для ∀х
∋
Х
выполняется неравенство х
> М,
то множество Х
называется ограниченным снизу (числом
m).
Число m
называется нижней границей множества
Х.
3.4.3.Если
существует число М
∈
R
такое, что для ∀х
∋
Х
выполняется неравенство |х|
< М,
то множество Х
называется ограниченным.
Теорема
3.4.1.
Множество ограничено тогда и только
тогда, когда оно ограничено сверху и
снизу.
Если
множество Х
ограничено сверху, то множество его
верхних границ бесконечно (если число
М
- верхняя граница, то верхними границами
будут числа М
+ 1, М
+ 2 и т.д.). Обозначим У
множество верхних границ множества Х.
Множество У
ограничено снизу (любым элементом
множества Х).
Возможны
два случая: либо множество Х
имеет максимальный элемент (например,
если Х
- отрезок [0, 1], то максимальный элемент
равен 1), в этом случае множество верхних
границ не имеет минимального элемента;
либо множество Х
не имеет максимального элемента
(например, если Х
= (0, 1)), в этом случае множество верхних
границ имеет минимальный элемент.
Определение
3.4.4. Точной верхней границей,
или верхней
гранью,
множества Х,
ограниченного сверху, называется
максимальный элемент этого множества,
если он существует, и минимальный элемент
множества верхних границ, если множество
Х
не имеет максимального элемента.
Для
обозначения применяются: символы sup X
или sup{x}.
Свойства
верхней грани:
Пусть М*=
sup X - верхняя грань множества Х. Тогда
3.4.2.
Для ∀х
∈
Х
выполняется неравенство х
≤ М*.
3.4.3.
Любое число, меньшее М*, не будет верхней
границей множества Х,
т.е. для ∀ε
> 0 ∃x
∈
X
такой, что х
> М*-ε.
Аналогичным
образом, если множество Х
ограничено снизу, то множество его
нижних границ бесконечно. Обозначим Z
множество нижних границ множества Х.
Множество Z
ограничено сверху (любым элементом
множества Х).
Определение
3.4.5. Точной нижней границей,
или нижней
гранью,
множества Х,
ограниченного снизу, называется
минимальный элемент этого множества,
если он существует, и максимальный
элемент множества нижних границ, если
множество Х
не имеет минимального элемента.
Для
обозначения применяются: символы inf X
или inf{x}.
Свойства
нижней грани:
Пусть М*=
inf X
- нижняя грань множества Х.
Тогда
3.4.2.
Для ∀х
∈
Х
выполняется неравенство х
≥ М*.
3.4.3.
Любое число, большее М*,
не будет нижней границей множества Х,
т.е. для ∀ε
> 0 ∃x
∈
X
такой, что х
< М* + ε.
4. Предел функции одной переменной.
4.1. Определение функции. Терминология.
4.2.
Гиперболические функции.
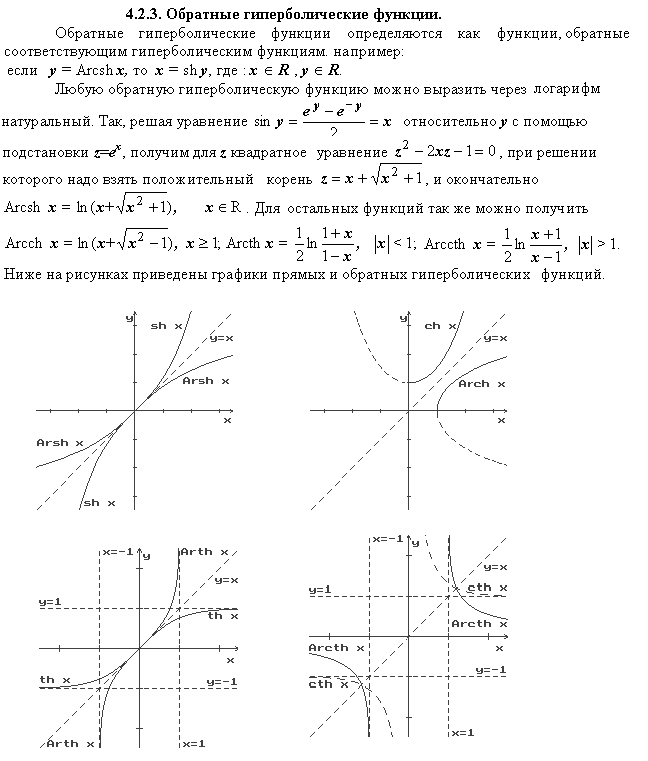
4.2.1. Определение гиперболических функций. 4.2.2. Соотношения между гиперболическими функциями. 4.2.3. Обратные гиперболические функции
4.2.1.
Определение гиперболических функций.
4.3. Последовательность и её предел.
4.3.1. Определение последовательности и её предела. 4.3.2. Свойства сходящейся последовательности. 4.3.3. Число e.
5. Непрерывность функций.
5.1. Определение непрерывность функции в точке.
-
5.1.1. Основное определение непрерывности функции в точке.
-
5.1.2. Определение в терминах
.
-
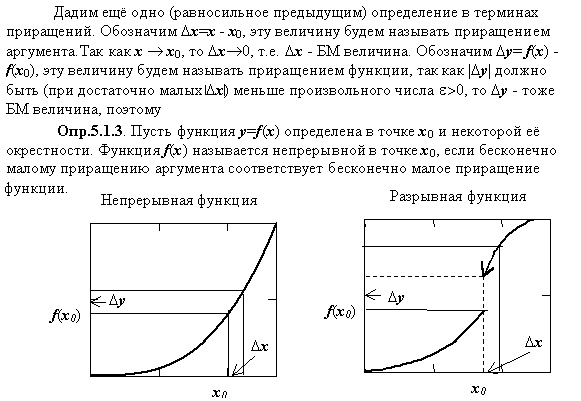
5.1.3. Определение в терминах приращений.
-
5.1.4. Определение в терминах последовательностей.
-
5.1.5. Определение разрывной функции.
-
5.1.6. Определение функции, непрерывной на множестве.
5.2. Определение непрерывность функции в точке.
-
5.2.1. Теорема о непрерывности суммы, произведения и частного непрерывных функций.
-
5.2.2. Теорема о переходе к пределу под знаком непрерывной функции.
-
5.2.3. Теорема о непрерывности суперпозиции непрерывных функций.
.3. Непрерывность элементарных функций.
-
5.3.1. Непрерывность рациональной и дробно-рациональной функций.
-
5.3.2. Непрерывность показательной и логарифмической функций.
-
5.3.3. Непрерывность тригонометрических функций.
-
5.3.4. Непрерывность гиперболических функций.
-
5.3.5. Непрерывность показательно-степенной функции..
