Министерство высшего и профессионального образования РФ

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Кафедра УИТ

КУРСОВАЯ РАБОТА

по курсу:

“Математические основы теории систем”

Построение и анализ математической модели объекта управления

Выполнил ст. гр. УИТ 42в

Проверил преподаватель

.

БАЛАКОВО 2003

№ варианта	Параметры элементов эквивалентной схемы объекта управления										Выходная переменная
18	R1 Ом	R2 Ом	R3 Ом	R4 Ом	R5 Ом	L1 Гн	L2 Гн	L3 Гн	C1 мкФ	C2 мкФ	i3
	342	437	132	182		25	25			18839

Эквивалентная схема объекта управления

L₁ e(t) L₂

i2 R₁ i1 R₂ i3 C₂

R₃ R₄

1. Построить математическую модель объекта управления в пространстве состояния

Эквивалентная электрическая схема объекта управления приведения на рис. 1.

L₁ e(t) L₂

i2 R₁ i1 R₂ i3 C₂

R₃ R₄

Рис.1. Эквивалентная схема объекта управления

1. Структурная схема объекта управления

В схеме три элемента, запасающих энергию, следовательно, математическая модель должна быть третьего порядка.

При построении математических моделей необходимо учитывать следующие выражения для связи токов, напряжений и комплексных сопротивлений элементов электрической схемы:

Для сопротивления R Е=1*R I= Z_R=R

Для индуктивности L E=L* I= Z_L=pI

Для емкости С E= I=C Z_C=

2. Построение математической модели.

0. Задаемся направлением контурных токов i1, i2, i3.

1. Составляем три уравнения по второму закону Кирхгофа.

(R1+R2)i1-R1i2-R2i3=e (1)

(R1+R4)i2+L1-R1i1=0 (2)

(R2+R4)i3+L2-R2i1=0 (3)

Продифференцируем уравнение (3), чтобы уйти от интеграла

(R2+R4)+L2+-R2=0 (3.2)

2.3. Введем вектор состояния объекта управления х1,х2,х3.

х1=(R2+R4)i3+L2-R2i1 (3.2)

Здесь из уравнения (3.1) взяты элементы, содержащие производные, но на 1 порядок ниже. В уравнении (3.2) имеются еще производные, поэтому:

х2=L2i3 отсюда i3=

В уравнении (2) также имеется производная, поэтому вводим:

х3=L1i2 отсюда i2=

Запишем введенный вектор состояния в виде дифференциальных уравнений 1-го порядка

=(R2+R4) i3+L2-R2i1 (4)

х2= L2i3 (5)

х3= L1i2 (6)

Первые части этих уравнений находятся в выражениях (3.1), (3.2) и (2). Внесем эти элементы в данных выражения в левые части и заменим производными вектора состояни. Тогда из выражения (3.1), (3.2) и (2) с учетом (4), (5), (6) получим:

х1=-

х2= х1-(R2+R4)i3+R2i1

x3=R1i1-(R1=R3)i2

Выразим i2,i3 через полученные ранее выражения. i1 выразим из (1).

i1=

i1=

Тогда

х1=-

х2=х1-

х2=х1-

х3=

х3=

Приведя подобные члены, перепишем:

х1=-

х2=х1-

х3=

Запишем систему дифференциальных уравнений в матричном виде

Х=АХ+ВХ

3. Построение графа системы и нахождение передаточной функции

Перепишем уравнения в обобщенном виде для построения графа системы

х1=а12х2

х2=а21х1+а22х2+а23х3+b21е

х3=а32х2+а33х3+b31е

i3=c12x2

Построение графа производим в два шага.

Шаг1. Ставим точки входа, выхода системы U, i3 и векторы параметров х1, х2, х3.

Найдем передаточную функцию системы по формуле Мейсона

k – количество возможных путей от входа к выходу

- определитель графа

Рk – коэффициент передачи k пути от входа к выходу

k – определитель всех касающихся контуров при удалении k-го пути

=1 – (сумма коэффициентов передачи всех отдельных контуров)+(сумма всех возможных произведений из 2-х некасающихся контуров)-(сумма всех возможных комбинаций из 3-х некасающихся контуров)

Последовательность нахождения W(p) по формуле Мейсона.

1.Определить и записать уравнения всех k путей от входа к выходу Р1,Р2,…, Рk.

2. Выявить все n замкнутых контуров и записать их уравнения: L1,L2,…Ln.

3. Записать выражение для определителя .

4. Записать сомножители: .

5. Записать и преобразовать выражение передаточной функции W(p).

1. В данном случае имеются два пути от входа к выходу:

Р1=

Р2=

2. В системе имеется 4 замкнутых контура:

L1= L3=

L2= L4=

3.Определитель системы включает 4 контура и две пары некасающихся контуров L1,L2 и L1,L4

= 1-L1-L2-L3-L4+L1L2+L1L4

4. С омножители i. Их количество равно количеству прямых путей. Выражение для i записывается как выражение для , но разрываются контура через которые проходит прямой путь Рi.

Сомножитель 1 для первого пути. При размыкании первого пути все 4 контура размыкаются, поэтому все Li становятся равными 0.

1=0

Сомножитель 2 для второго пути. при размыкании второго пути разрываются контура кроме L1.

2=1-L1

5. Запишем и преобразуем выражение передаточной функции:

W(p)=

W(p)=

W(p)=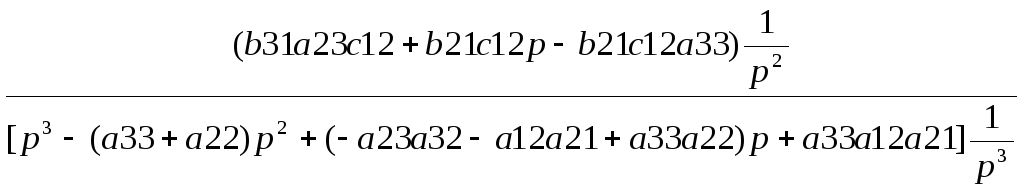

W(p)=

После подстановки значений коэффициентов передаточная функция

имеет вид:

W(p)=