Построение матрицы планирования
Определим интервал варьирования по выражению:
.
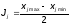(1)
Таблица №1
Уровни факторов и интервалы варьирования
|
Уровни факторов |
Факторы процесса |
|||
|
X1 |
X2 |
X3 |
X4 |
|
|
Нижний |
6 |
70 |
0,22 |
12 |
|
Основной |
8 |
75 |
0,36 |
32 |
|
Верхний |
10 |
80 |
0,5 |
52 |
|
Уровни варьирования |
2 |
5 |
0,14 |
20 |
|
№ точки плана |
Факторы |
S2 |
S |
Dy |
Значение параметра оптимизации |
||||||||||||
|
X1 |
X2 |
X3 |
X4 |
|
|
|
Yср |
Y1 |
Y2 |
Y3 |
Y4 |
||||||
|
1 |
- |
- |
- |
- |
0,01193125 |
0,1092303 |
0,039688 |
0,3675 |
0,12 |
1,1 |
0,11 |
0,14 |
|||||
|
2 |
+ |
- |
- |
- |
0,00000833 |
0,0028868 |
0,004225 |
0,065 |
0,06 |
0,05 |
0,07 |
0,08 |
|||||
|
3 |
- |
+ |
- |
- |
0,00001458 |
0,0038188 |
0,039006 |
0,1975 |
0,19 |
0,18 |
0,22 |
0,2 |
|||||
|
4 |
+ |
+ |
- |
- |
0,00001125 |
0,0033541 |
0,029756 |
0,1725 |
0,19 |
0,16 |
0,18 |
0,16 |
|||||
|
5 |
- |
- |
+ |
- |
0,00001458 |
0,0038188 |
0,018906 |
0,1375 |
0,13 |
0,12 |
0,14 |
0,16 |
|||||
|
6 |
+ |
- |
+ |
- |
0,00000833 |
0,0028868 |
0,011025 |
0,105 |
0,11 |
0,12 |
0,09 |
0,1 |
|||||
|
7 |
- |
+ |
+ |
- |
0,00000833 |
0,0028868 |
0,050625 |
0,225 |
0,24 |
0,23 |
0,22 |
0,21 |
|||||
|
8 |
+ |
+ |
+ |
- |
0,00000833 |
0,0028868 |
0,013225 |
0,115 |
0,12 |
0,11 |
0,1 |
0,13 |
|||||
|
9 |
- |
- |
- |
+ |
0,00001458 |
0,0038188 |
0,003306 |
0,0575 |
0,04 |
0,06 |
0,05 |
0,08 |
|||||
|
10 |
+ |
- |
- |
+ |
0,00000833 |
0,0028868 |
0,038025 |
0,195 |
0,18 |
0,19 |
0,2 |
0,21 |
|||||
|
11 |
- |
+ |
- |
+ |
0,00001667 |
0,0040825 |
0,0256 |
0,16 |
0,18 |
0,14 |
0,15 |
0,17 |
|||||
|
12 |
+ |
+ |
- |
+ |
0,00001667 |
0,0040825 |
0,0225 |
0,15 |
0,13 |
0,14 |
0,16 |
0,17 |
|||||
|
13 |
- |
- |
+ |
+ |
0,00000833 |
0,0028868 |
0,011025 |
0,105 |
0,11 |
0,12 |
0,09 |
0,1 |
|||||
|
14 |
+ |
- |
+ |
+ |
0,00003500 |
0,0059161 |
0,055225 |
0,235 |
0,26 |
0,25 |
0,23 |
0,2 |
|||||
|
15 |
- |
+ |
+ |
+ |
0,00003792 |
0,0061577 |
0,041006 |
0,2025 |
0,22 |
0,23 |
0,19 |
0,17 |
|||||
|
16 |
+ |
+ |
+ |
+ |
0,00001458 |
0,0038188 |
0,041006 |
0,2025 |
0,2 |
0,22 |
0,21 |
0,18 |
|||||
Таблица №2
Определим ошибки опыта по следующим показателям:
1. Среднее арифметическое результатов:
=
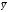(y1
+ y2
+ y3
+ . . . + yn)
/ n =
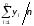(2)
где уl - результаты экспериментов, n - количество опытов в серии.
n = 4;
2. Дисперсия - среднее значение квадрата отклонений величины от ее среднего значения:
,
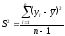(3)
где (n-1) - число степеней свободы, равное количеству параллельных опытов минус единица.
3. Квадратичная ошибка или стандарт:
.
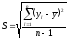Проверяем первую серию опытов на наличие ошибки.
Для определения ошибок опыта используем критерий Стьюдента:
;
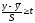S = 0,10923026
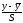=6.7t=2.78,
где t - коэффициент Стьюдента. А значит значение опыта равное 1.1 - промах и из дальнейшего рассмотрения мы его исключаем.
Проверяем дисперсию на однородность:
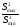=0,00003792/0.00000833=4.552208884
Полученное значение больше табличного значения критерия Фишера, значит дисперсии неоднородны.
Находим дисперсию выходного параметра или параметра оптимизации:
=
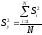0,00004749
Расчет линейной части.
Записываем уравнение процесса в виде:
Y = b0 +b1x1 + b2x2 +b3x3+b4x4
Коэффициент b0 находится по формуле
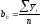
Таблица №3
|
|
b0 |
b1 |
b2 |
b3 |
b4 |
|
Yср1 |
0,3675 |
-0,368 |
-0,368 |
-0,368 |
-0,368 |
|
Yср2 |
0,065 |
0,065 |
-0,065 |
-0,065 |
-0,065 |
|
Yср3 |
0,1975 |
-0,198 |
0,1975 |
-0,198 |
-0,198 |
|
Yср4 |
0,1725 |
0,1725 |
0,1725 |
-0,173 |
-0,173 |
|
Yср5 |
0,1375 |
-0,138 |
-0,138 |
0,1375 |
-0,138 |
|
Yср6 |
0,105 |
0,105 |
-0,105 |
0,105 |
-0,105 |
|
Yср7 |
0,225 |
-0,225 |
0,225 |
0,225 |
-0,225 |
|
Yср8 |
0,115 |
0,115 |
0,115 |
0,115 |
-0,115 |
|
Yср9 |
0,0575 |
-0,058 |
-0,058 |
-0,058 |
0,0575 |
|
Yср10 |
0,195 |
0,195 |
-0,195 |
-0,195 |
0,195 |
|
Yср11 |
0,16 |
-0,16 |
0,16 |
-0,16 |
0,16 |
|
Yср12 |
0,15 |
0,15 |
0,15 |
-0,15 |
0,15 |
|
Yср13 |
0,105 |
-0,105 |
-0,105 |
0,105 |
0,105 |
|
Yср14 |
0,235 |
0,235 |
-0,235 |
0,235 |
0,235 |
|
Yср15 |
0,2025 |
-0,203 |
0,2025 |
0,2025 |
0,2025 |
|
Yср16 |
0,2025 |
0,2025 |
0,2025 |
0,2025 |
0,2025 |
|
|
0,16828 |
-0,0133 |
0,00984 |
-0,0023 |
-0,0048 |
С учетом произведенных расчетов линейная модель примет вид:
Y = 0,16828-0,0133x1 + 0,00984x2 -0,0023x3-0,0048x4
Найдем квадрат отклонения расчетного значения от экспериментального:
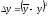
данные занесем в таблицу №2 (см вверх)