Саратовский Государственный Технический Университет

Балаковский Институт Техники Технологии и Управления

Кафедра:УИТ

Специальность: УИТ

Курсовая работа

По дисциплине

Математические основы теории систем

Вариант №14

Выполнил:

Принял:

Балаково 2009

Содержание

Задание _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _3

1-часть.

1. Построение математической модели объекта управления в пространстве состояния. _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _4

2. Построение математической модели. _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _4

3. Построение сигнального графа. _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _7

4. Нахождение передаточной функции по формуле Мейсона. _ _ _ _ _10

Часть 2

1. Расчет корреляционной функции _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 14

2. Расчет статистической характеристики _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _15

3. Нахождение общей передаточной функции _ _ _ _ _ _ _ _ _ _ _ _ _ _17

Вывод _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 19

1-часть.

Задание1: По виду электрической схемы построить математическую модель объекта управления в пространстве состояния.

Задание2: По построенной модели составить структурную схему и сигнальный граф.

Задание3: Используя формулу Мейсона найти передаточную функцию объекта управления.

Задание4: По передаточной функции объекта управления определить временные и частотные характеристики. Построить их зависимость: АЧХ, ФЧХ.

Задание5: По полученным зависимостям определить прямые и косвенные оценки качества объекта управления.

2-часть.

Задание1: По заданной корреляционной функции Kx() определить спектральную плотность Sx() для белого шума, который подается на вход формирующего фильтра.

Задание2: По заданным статистическим характеристикам Se, Sv определить передаточную функцию формирующего фильтра (р)

Задание3: Представить объект управления в виде

V(t) X(t) Y(t)

и оценить качество полученной системы по переходной характеристике.

Задание4: Сделать вывод по работе.

Вариант №14

Часть 1

Данные

R1	R2	R3	R4	R6	L2		L3	C1		C2
Ом						Гн.			10-6Ф
330	389	112	176	112	23		49	42602		21555

выходной параметр i4.

Рис.1 Эквивалентная схема объекта управления

1. Построим математическую модель объекта управления в пространстве состояния.

е i4

В схеме четыре элемента, запасающих энергию:L1,L2,C1,C2, следовательно, математическая модель должна быть четвертого порядка.

2. Построение математической модели.

Задаемся направлением контурных токов i1,i2,i3,i4. Составляем четыре уравнения по второму закону Кирхгофа для контуров:

В уравнениях (1),(4) есть интегралы, поэтому дифференцируем их:

В уравнениях есть производные, в качестве x1,x2,x3,x4 выбираем элементы с производными и производные берем на порядок ниже:

Запишем введенный вектор состояния в виде дифференциальных уравнений первого порядка.

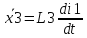
Уравнение в пространстве состояний записывается в левой части:

Выразим токи i1,i2,i3,i4:

Найдем

выходной параметр:

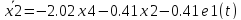
Получили четыре дифференциальных уравнения и одно уравнение для выходного параметра.

Запишем полученную систему уравнений в матричном виде:

Получим матричное уравнение для выходной переменной:

3. Построение сигнального графа.

Перепишем уравнения в общем, виде для построения графа системы:

Рис.2 Сигнальный граф

Рис.3 Объединенный сигнальный граф

Рис. 4 Структурная схема

3. Нахождение передаточной функции по формуле Мейсона.

k-количество возможных путей от входа к выходу

-определитель графа

P_k-коэффициент передачи k пути от входа к выходу

-определитель всех касающихся контуров при удалении k-ого пути

=1-(сумма коэффициентов передачи всех отдельных контуров)+(сумма всевозможных произведений из двух некасающихся контуров) - (сумма всевозможных комбинаций из трех некасающихся контуров)+…+…

Последовательность нахождения w(p) по формуле Мейсена:

В данном случае есть 4 пути от входа к выходу:

В системе имеется 7 замкнутых контуров:

Количество сомножителей равно количеству прямых путей. Выражение для 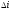записывается как выражение для , но разрываются контуры, через которые проходит прямой путь P_i.

Запишем и преобразуем выражение передаточной функции:

Рис. 5 график переходной функции

Рис. 6 график импульсной переходной функции

Рис. 7 график АЧХ

Рис.8 график ФЧХ

По графикам переходной функции и АЧХ определим прямые и косвенные оценки качества системы.

Прямые оценки: невозможно определить

Косвенные оценки:

1) Показатель колебательности

2) Резонансная частота

3) Полоса пропускания частот

Часть 2

1. Дана корреляционная функция

Рис.8 график корреляционной функции

Тогда спектральная плотность для белого шума, который подается на вход формирующего фильтра:

Рис.9 график формирующего фильтра

2. Даны статистические характеристики и

Передаточная функция формирующего фильтра определяется следующим выражением:

Найдем корни числителя и знаменателя .

Рис. 10

Для записи передаточной функции выберем корни, с положительной мнимой частью.

Так как сомножитель знаменателя образуется из решения уравнения , то его можно заменить непосредственно этим уравнением.

Получаем:

_{Произведем замену}

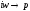
3. Общая передаточная функция:

Wоб(p)=ψ(p)*W(p)

Определим переходную характеристику данной системы и отобразим ее графически:

Рис. 11 график общей передаточной функции.

По данной зависимости видно, что система не устойчива, следовательно, невозможно определение параметров качества ( и др.)

Рис.12 график общей АЧХ

Косвенные оценки:

1) Показатель колебательности

2) Резонансная частота

3) Полоса пропускания частот

Из проведенного анализа математической модели объекта управления в пространстве состояний, который включает в себя определение прямых и косвенных оценок качества системы, следует:

Что система до применения формирующего фильтра имела косвенные оценки качества

1) Показатель колебательности

2) Резонансная частота

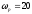
3) Полоса пропускания частот

После применения формирующего фильтра стала иметь следующие косвенные оценки качества

1) Показатель колебательности

2) Резонансная частота

3) Полоса пропускания частот

По переходному процессу система не изменилась, т.е. осталась неустойчивой.