56

а₀[y₁(k+2)₁(k)+ y₂(k+2)₂(k)] + ₁(k)[a₀ y₁(k+2)+ a₁ y₁(k+1)+

+ a₂ y₁(k)]+ ₂(k)[a₀ y₂(k+2)+ a₁ y₂(k+1)+ a₂ y₂(k)] = F(k).

Поскольку y₁(k)иy₂(k)суть решения соответствующего однородного уравнения, то из последней формулы имеем

y₁(k+2)₁(k)+ y₂(k+2)₂(k) = F(k)/a₀. (2.32)

Теперь осталось решить систему уравнений (2.32) и (2.31) относительно неизвестных ₁(k)и₂(k)

и определить сами функции ₁(k) и ₂(k):

(2.33)

Знаменатели в (2.33) отличны от нуля, так как y₁(k) и y₂(k)– независимые решения однородного уравнения, а следовательно, выполняется условие (2.20).

Обобщим результаты решений уравнений первого и второго порядка на уравнение произвольного порядка (2.17).

Общее решение однородного уравнения берем в виде (2.21). Тогда частное решение ищется в форме

y_H (k) = ₁(k)y₁(k) +…+ _n(k)y_n(k) . (2.34)

Одно из условий, накладываемых на функции _i(k), -это удовлетворение исходного уравнения (2.17), а остальныеn-1условий определяются уравнениями, аналогичными уравнению(2.31):

y₁ (k+1) ₁(k) + y₂(k+1) ₂(k) +…+ y_n(k+1) _n(k) = 0;

y₁ (k+2) ₁(k) + y₂(k+2) ₂(k) +…+ y_n(k+2) _n(k) = 0;

.

.

.

y₁ (k+n-1) ₁(k) + …+ y_n(k+n-1) _n(k) = 0. (2.35)

Подставляя решение (2.34) в уравнение (2.17) и учитывая (2.35), после соответствующих преобразований будем иметь

y₁ (k+n) ₁(k) + y₂(k+n) ₂(k) +…+ y_n(k+n) _n(k) = F(k)/a_0. (2.36)

Решая систему из n уравнений (2.35) и (2.36), находим

или

(2.37)

где С(k) – определитель Касорати, а С_ni(k) – алгебраические дополнения ni – ых элементов. Из условия (2.20) следует, что С(k) отличен от нуля, если y₁(k)  y_n(k) - линейно независимые решения однородного уравнения.

Выражение (2.37) дает в явном виде решение y_Н(k) по известному y₀(k) для произвольной вынуждающей функции F(k), хотя в некоторых случаях трудно представить в замкнутом виде входящую в формулу (2.37) сумму. Метод вариации параметров позволяет находить решение и разностных уравнений с переменными коэффициентами, то есть уравнений, описывающих нестационарные во времени системы. Завершая этот подраздел, введем понятие передаточной функции дискретной во времени системы.

Решим формально уравнение (2.15) или (2.16) относительно выхода y(k):

(2.38)

Идентифицируем оператор Ес некоторой независимой переменнойz. Тогда характеристикой системы, описываемой уравнением (2.15), будет отношение полиномовB(z) к A(z):

(2.39)

Последнее соотношение и определяет формально передаточную функцию дискретной системы (другие названия – «импульсная передаточная функция», «дискретная передаточная функция»). Более строго импульсная передаточная функция будет определена чуть дальше с использованием z - преобразования.

2.3 Дискретное преобразование Лапласа

Для исследования непрерывных систем широко применяется преобразование Лапласа. Но непосредственное применение преобразования Лапласа к разностному уравнению и, в частности, к любой решетчатой функции f(kT) тождественно дает нуль, так как площадь этой функции ( или в физической интерпретации – энергия такого сигнала) равна нулю. Чтобы выйти из этого затруднительного положения, придадим функции f(kT) площадь, равную значению этой функции. Проще всего это сделать, умножив значение функции в точке t = kT на дельта – функцию, принимающую бесконечное значение в этой же точке. Проделав такую операцию для всех k, при которых определена функция f, получим импульсную функцию

(2.40)

представляющую собой последовательность «идеальных» импульсов с бесконечной амплитудой и бесконечно малой длительностью, причем каждый импульс имеет площадь, равную значению функции f(kT). Точно такую же импульсную функцию можно получить и из непрерывной функции f(t), применив к ней формулу (2.40)

(2.41)

где через δ_Т(t) обозначена соответствующая сумма δ – функций.

Воспользовавшись выражением (2.41) можно дать одно из понятий дискретного преобразования Лапласа, наиболее удобное с инженерных позиций. Определим дискретное преобразование Лапласа функции f(t) как преобразование Лапласа от импульсной функции f^*(t), соответствующей непрерывной функции f(t):

(2.42)

Преимущество такого определения состоит в том, что эта новая операция полностью выражается через уже знакомую и хорошо изученную операцию обычного преобразования Лапласа.

Согласно (2.42) и с учетом (2.41) имеем

Поменяв в правой части последнего выражения порядок интегрирования и суммирования, получим

(2.43)

В формуле (2.43) отсутствует δ– функция, и она может быть использована непосредственно для решетчатой функции.

Нетрудно получить альтернативную формулу для вычисления дискретного преобразования Лапласа функции f(t) по ее обычному преобразованию Лапласа.

Опять воспользуемся выражениями (2.41) и (2.42).

Имеем

Для вычисления правой части последнего выражения используем теорему свертки в области изображений (см. формулу (1.54)); учитывая, что

Ряд в правой части последнего выражения сходится при |e^-sT| < 1, т.е. при Re s>0 и его сумма равна 1/1-e^-Ts (сумма геометрической прогрессии).

Таким образом, получим

(2.44)

При записи выражения (2.44) использована формула (1.54), причем в качестве функций F₁(s), F₂(s) взяты соответственно 1/1-e^-Ts и F(s), а величина с удовлетворяет соотношениям (1.54') и (1.54''), следовательно, все полюсы функции F(s) лежат левее линии интегрирования. Абсцисса абсолютной сходимости функции _Т(t) , представляющей сумму  - функции, как известно, равна нулю, следовательно, для сходимости интеграла (2.44) требуется, чтобы Re s > c. Из выражения (2.44) следует, что дискретное преобразование Лапласа существует для всех функций, для которых существует и обычное преобразование Лапласа.

Вычислить интеграл (2.44) можно, воспользовавшись теоремой о вычетах (теорема Коши), как сумму вычетов подинтегрального выражения в его полюсах, расположенных внутри контура интегрирования, который не должен иметь на себе особенностей подинтегрального выражения. Для этого необходимо замкнуть путь интегрирования. Это можно сделать, добавив к пути интегрирования бесконечно большую полуокружность либо в левой полуплоскости (R -) либо в правой (R +), как показано на рисунке 2.1. При этом получим замкнутый контур Г₁, либо Г₂.

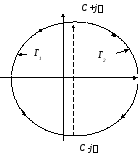
Рисунок 2.1

В первом случае (контур Г₁) имеем

(2.45)

где _{i –} полюсы функции F(s), так как внутри контура Г₁ расположены только они.