Тогда получим

Q(w) = w₁² + w₂² +…+ w_p² - w_p+1²-…- w_r². (3.63)

Формулу (3.63) можно рассматривать как прямое следствие приведения к канонической форме (3.43).

Эрмитова форма ранга r приводится к диагональному виду подобным образом:

Q(w) = w₁* w₁+ w₂* w₂+…+ w_p*w_p - w_p+1*w_p+1-…- w_r*w_r.

Последнее выражение вытекает из определения канонической формы (3.45).

3.5.2 Определенные, полуопределенные и неопределенные

формы

Квадратичная форма Q(x)= <x,Ax> называется положительно определенной, если она положительна при всех х, исключая х=0. Конгруэнтные преобразования (впрочем, как и любые эквивалентные преобразования) не меняют положительной определенности формы, поэтому из соотношения (3.63) следует, что квадратичная форма будет положительно определенной, если и только если А является неособенной матрицей, и индекс формы (то есть число положительных членов) равен ее рангу, т.е. p = r = n. Из уравнения (3.61) ясно, что квадратичная форма положительно определена в том и только в том случае, когда все собственные числа матрицы А положительные _i>0 (i=1,2,…n). Любое из этих условий может быть использовано при определении положительной определенности квадратичной формы.

Квадратичная форма называется положительно полуопределенной, если она не отрицательна для всех х и существуют х 0, для которых Q(x) =0. Такое будет тогда и только тогда, когда все собственные значения А неотрицательны и, по крайней мере, одно из собственных значений равно нулю. При этом матрица А , согласно (3.30), будет особенной и ее ранг r < n.

Подобные утверждения могут быть сделаны и относительно отрицательно определенных и отрицательно полуопределенных квадратичных форм. Квадратичная форма Q(x) называется отрицательно определенной, если она отрицательна для всех х, исключая x = 0. Квадратичная форма Q(x) будет являться отрицательно полуопределенной, если она не положительна для всех х и существуют точки х 0, для которых Q(x) =0.

Квадратичная форма является неопределенной тогда и только тогда, когда матрица А имеет как положительные, так и отрицательные собственные числа. При этом в векторном пространстве V_n можно найти такие точки, в которых квадратичная форма будет иметь противоположные знаки.

Устанавливать определенность квадратичной формы по собственным значениям матрицы А или путем приведения А к канонической форме достаточно сложно при больших размерностях А, поэтому разработан более простой критерий по установлению положительной определенности квадратичной формы. Можно показать, что для того, чтобы квадратичная форма х^ТАх или симметрическая матрица А были положительно определенными, необходимо и достаточно, чтобы расположенные в естественном порядке все ее главные миноры были положительны, т.е.

₁ = a₁₁ > 0, ₂ =

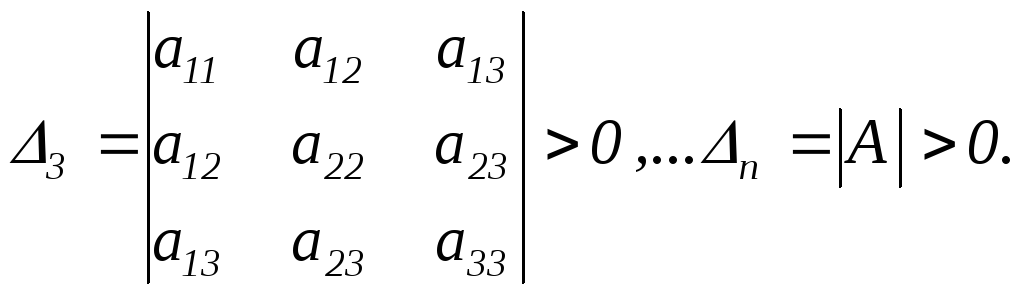
Эти главные миноры А называются также дискриминантами квадратичной формы.

Для эрмитовых форм существуют аналогичные формулировки.

Условия отрицательной определенности могут быть получены, если потребовать положительную определенность (­А).