3.5 Квадратичные формы

Билинейной формой от n переменных х₁, x₂,…x_n и n переменных y₁, y₂,…y_n называется сумма вида

B = a₁₁x₁y₁ + a₁₂x₁y₂ +…+ a_1nx₁y_n +

+ a₂₁x₂y₁ + a₂₂x₂y₂ +…+ a_2nx₂y_n +

………. (3.56)

+ a_n1x_ny₁ + a_n2x_ny₂ +…+ a_nnx_ny_n =

где все составляющие – действительные числа. Билинейную форму удобно изображать в матричной записи

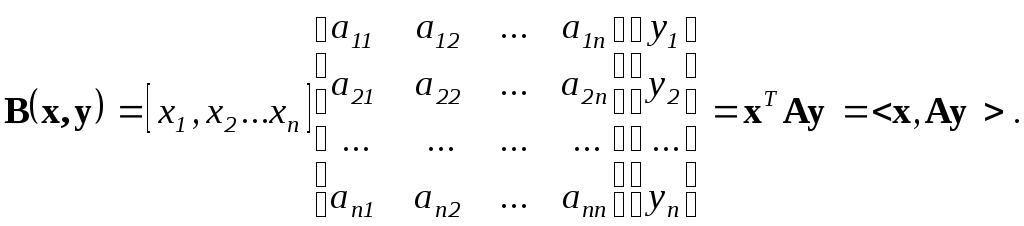
(3.57)

Матрица А называется матрицей коэффициентов формы или просто матрицей формы, а ранг А – рангом формы.

Если в выражении (3.57) положить х=у, то получим

Q(x) = x^TAx = <x,Ax> = (3.58)

Выражение (3.58) называется квадратичной формой от переменных x₁,x₂,…x_n. Нетрудно видеть, что коэффициент при произведении x_{i } x_j (ij) равен (a_ij +a_ji). Этот коэффициент не изменится, если оба a_ij и a_ji положить равными (a_ij + a_ji)/2. Поэтому, ничуть не снижая общности, можно считать матрицу А симметрической.

Если матрица А является эрмитовой, то соответствующую эрмитову форму можно определить как

H(x) = <x,Ax> = (x^T)*Ax = (3.59)

3.5.1 Преобразование переменных

Перейдем в выражении (3.58) от переменных x_i к переменным y_i с помощью преобразования х=Bу, где B – произвольная неособенная квадратная матрица размерностью n. Получим в результате квадратичную форму от переменных y₁,y₂,…y_n:

Q = y^TB^TAВy=y^T Cy, (3.60)

где С = B^ТАB является конгруэнтным преобразованием, так что ранг формы не меняется.

Во многих случаях желательно выразить Q в виде линейной комбинации только квадратов координат. Это будет, очевидно, в том случае, если матрицу А привести к диагональному виду. Особенно полезным оказывается ортогональное преобразование, т.е. когда B является ортогональной матрицей (B^Т = B^-1). Как уже было выяснено в предыдущем подразделе, такое возможно для симметрических матриц А, если в качестве матрицы B взять модальную матрицу М. Таким образом, линейное преобразование х= Му приводит к квадратичной форме

Q(y) =y^TM ^-1AMy=y^Ty=₁y₁²+₂y₂²+…+_ny_n². (3.61)

Если у симметрической матрицы А ранг r < n, и имеются кратные собственные значения, то по – прежнему модальная матрица может быть составлена из линейно независимых столбцов и в результате преобразование приведет к диагональной матрице. В этом случае модальная матрица М не единственная и, согласно свойствам симметрических матриц, существует бесконечное множество систем m ортогональных собственных векторов, соответствующих собственному числу кратности m. В результате преобразования в квадратичной форме (3.61) останется только r слагаемых.

В случае, если конгруэнтное преобразование неортогональное, квадратичную форму можно привести к виду

Q(z) = ₁z₁² + ₂z₂² +…+ _pz_p² - _p+1z_p+1² -…- _nz_n², (3.62)

где _i (i=1,2,…n) – положительные числа. Число положительных членов p называется индексом квадратичной формы.

Если квадратичная форма имеет ранг r  n, то в выражении (3.62) остается только r членов. Форму (3.62) можно еще упростить, если ввести невырожденное преобразование