103

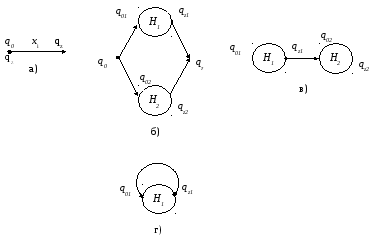
Рис. 4.1

в вершину q_z. И наоборот, всякий путь х из q₀ в q_z обязательно проходит через q₀₁ и q_z1, либо через q₀₂ и q_z2 и имеет вид х = х₁  х₂, где х₁ – путь из q₀₁ в q_z1, а х₂ – путь из q₀₂ в q_z2, откуда следует, что х₁  Е₁ и х₂  Е₂ . Ч. т.д.

Пустые ребра вводятся для того, чтобы избежать ложных путей. Система правил, когда следует вводить пустые ребра в граф регулярного выражения следующая:

1. Пустые ребра вводятся в случае произведения двух или более итераций (рис. 4.2.), гдеR_i – регулярные выражения.

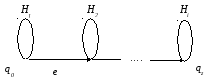Рис. 4.2

2. Пустые ребра в источнике, представляющем событие S, когда регулярное выражение для S начинается и заканчивается итерацией, вводятся в случаях:

а) S = (P^* R^* )^*,

б) S = (R N^* )^*,

в) S = (P^* R N^* )^*.

Здесь R, P и N – произвольные регулярные выражения.

Соответствующие графы изображены на рисунке 4.3.

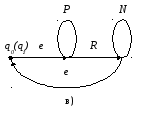
Рис 4.3

3. Пустые ребра вводятся в случае дизъюнкции, если хотя бы один из дизъюнктивных членов начинается с итерации

S = R^*  QP^* … Q,

где Q – регулярное выражение, не содержащее итерации (рис. 4.4).

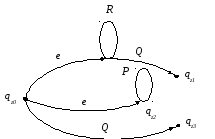
Рис. 4.4

4. Пустые ребра вводятся при умножении слева на дизъюнкцию, если хотя бы один из дизъюнктивных членов заканчивается итерацией (рис. 4.5.).

S = (Q  R*P* … Q)N.

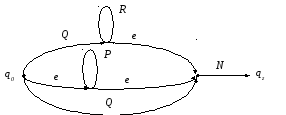
Рис. 4.5

Перечисленная система правил является полной, то есть в никаких других случаях вводить пустые ребра нет необходимости. Это нетрудно показать, рассматривая всевозможные сочетания операций (, , *) в регулярном выражении.

4.3.3 Синтез автоматов (абстрактный уровень)

Перейдем теперь к синтезу автоматов, то есть по сути к доказательству теоремы 4.3.2.а.

Вначале введем понятие детерминированного источника. Речь уже шла о том, что автомат без выходов – это частный случай источника. Источник будет являться графом автомата без выходов, если он: а) содержит одну начальную вершину, б) не содержит пустых ребер и в) удовлетворяет условиям автоматности. Такой источник и назовем детерминированным источником в отличие от произвольного недетерминированного источника. Это название связано с тем, что произвольный источник можно интерпретировать как недетерминированный автомат, то есть как автомат, в котором функция переходов (q, х) может иметь несколько значений (символу х при вершине q может соответствовать множество ребер, а слову х – множество путей из вершины q).

Теперь докажем вспомогательную теорему.

Теорема 4.3.4 (детерминизации). Для любого источника Н с n вершинами существует эквивалентный ему детерминированный источник Н, имеющий не более чем 2ⁿ вершин.

Доказательство. Назовем множество вершин замкнутым, если из того, чтоq_i, следует, что принадлежит любая вершина, в которую изq_i ведет пустое ребро. Таким образом, для источника без пустых ребер любое множество вершин замкнуто.

Источник Н' строится следующим образом. Образуем все замкнутые подмножества вершин Н (а их не более, чем 2ⁿ) и каждому такому подмножеству поставим в соответствие вершину _i источника Н'.

Через обозначим наименьшее замкнутое подмножество вершинН, содержащее все начальные вершины Н.

Это будет начальная вершина Н'. Заключительными вершинами Н' объявим все подмножества _i, содержащее хотя бы одну заключительную вершину Н. Если из множества _i источника Н есть пути х(хХ) в множество _j, то в источнике Н' соединяем вершину _i с вершиной _j ребром, на котором написан символ х. Если же в Н никакая из вершин _i не имеет выходящего из нее ребра с символом х, то соединяем вершину _i в Н' с вершиной Ø (пустое подмножество вершин Н) ребром х. Таким образом, каждой вершине _i в Н' и каждому символу х соответствует ровно одно ребро х, выходящее из _i, и источник Н' является детерминированным. Построение ребер Н' определяет функцию перехода автомата, граф которого – это источник Н'. Начальное состояние этого автомата ₁.

Осталось показать, что источник Н' эквивалентен Н. Действительно, Н' обладает свойством: в Н' непустой путь x из ₁ в _j существует тогда и только тогда, когда в Н для любой вершины q_j существует путь x из некоторой начальной вершины q₁₁ в q. Пустым путь x быть не может, так как, если x = е, то _j = ₁ по условию замкнутости и в Н' пустых ребер по построению нет. Это свойство доказывается индукцией по длине слова x.

Если x = х (состоит из одного символа), то это свойство выполняется по построению ребер в Н'. Предположим теперь, что оно выполняется и для слова длины  k и докажем, что оно выполняется и для слова xх, где хХ произвольная буква входного алфавита.

Пусть в Н' имеется непустой путь xх из ₁ в _j: δ(₁, xх) = _j. Если δ(₁, x) = _k, то из _k в _j ведет ребро х. По предположению, в Н для любой вершины q*_l существует путь x из начальной вершины q₁ в q*. По построению Н' из того, что в Н' есть ребро х из _k в _j, следует, что в Н для любой вершины q_i найдется вершина из подмножества _k, из которой ведет путь х в q, поэтому в Н имеется путь из q* в q и. следовательно, путь xх из q₁ в q.

И наоборот, если в Н для любой вершины q_i есть путь xх из начальной вершины q₁₁ в вершину q, то в Н' будет выполняться условие δ(₁, xх) = _j. Доказывается это аналогичным образом. При этом рассматривается множество путей xх из начальных вершин Н в вершины множества _i и множества _k всех вершин, в которые ведут отрезки x этих путей.

Из доказанного свойства Н' и определения заключительных вершин Н' следует, что в Н' путь x из ₁ в заключительную вершину есть тогда и только тогда, когда в Н имеется путь x из некоторой начальной вершины в заключительную. Следовательно, источники Н и Н' эквивалентны, поскольку представляют одно и то же событие. Что и требовалось доказать.

По сути дела, из доказательства теорем 4.3.3 и 4.3.4 и следует доказательство теоремы синтеза 4.3.2.а, а синтез автомата, представляющего произвольное регулярное событие Е, состоит в том, что сначала строится источник, представляющий Е, а затем этот источник детерминируется согласно процедуре, изложенной при доказательстве теоремы 4.3.4.

Практически детерминизация упрощается в связи с тем, что некоторые подмножества вершин Н (состояния Н') не достижимы из начального состояния и их удаление не изменит события, представляемого автоматом. Поэтому в матрицу переходов Н' включаются только те подмножества, которые порождаются процедурой детерминизации, начатой с подмножества ₁. В этом случае построенный автомат может иметь меньше чем 2ⁿ состояний.