Решение линейных разностных уравнений с изменяющимися во времени коэффициен­тами.

Рассмотрим разностное уравнение n-го порядка

[a_n(k)Eⁿ + a_n-1(k)E^n-1 +…+ a₁(k)E + a₀(k)]y(k) = F(k) (92)

Как и для дифференциальных уравнений, решение всегда опре­деляется для уравнений первого порядка и в общем случае не может быть найдено для уравнений более высокого порядка.

Вспомогательное решение.

Рассмотрим однородной уравнение первого порядка

a₁(k)y(k+1) + a₀(k)y(k) = 0, (93)

где a₀(k)≠0 и a₁(k)≠0. Его можно переписать в виде

y(k+1) = a(k)y(k). (94)

при k=0,1,2...

у(1)=а(0)у(0),

у(2)=а(1)а(0)у(0)

у(3)=а(2)а(1)а(0)у(0)

или, в общем случае,

, (95)

так что общее решение уравнения (94) равно

Нижний предел произведения произволен, так как любое фик­сированное число множителей а(0), а(1), и а(2), ... можно объединить с произвольной постоянной С.

Решение однородного уравнения выше первого порядка в общем случае не выражается в виде элементарных функций, так как процедура, основанная на уравнениях (81) и (82), при зависящих от k коэффициентах перестает быть справедливой. Если известны все, кроме одного, независимые решения уравнения, то можно определить и ос­тавшееся решение. Как и для дифференциальных уравнений, в ряде отдель­ных случаев удается получить, решение в явном виде. Уравнение вида

a_nf(k + n)y(k + n) + ... + a₁f (k + 1)y(k + 1) + a_nf(k)y(k) = 0,

где коэффициенты а_i - постоянные величины, путем подстановки z(k)=f(k)y(k) сводится к разностному уравнению с постоянными коэффициентами. Проце­дура отчасти сходна с используемой для дифференциального уравнения Эй­лера, но замене в данном случае подлежит зависимая (а не независимая) пе­ременная. Этот метод широко используется при решении уравнений с пе­ременными коэффициентами.

Дифференциальные уравнения систем автоматического регулирования. Методика составления дифференциальных уравнений систем автоматического регулирования.

Общие замечания.

Системы автоматического регулирования разнообразны по своему назначению и конструктивному исполнению. Поведение САР может описываться обыкновенными дифференциальными уравнениями в частных производных, разностными уравнениями и т.д.

Любая САР представляет совокупность отдельных взаимодействующих друг с другом элементов, соединенных между собой связями. Первым этапом при составлении дифференциальных уравнений САР является разделение системы на отдельные элементы и составление дифференциальных уравнений этих элементов. Уравнения элементов и уравнения связей между отдельными элементами описывают процесс в системе регулирования, т.е. изменение по времени всех координат системы. Зная уравнения элементов и уравнения связей, можно составить структурную схему САР.

Структурная схема САР характеризует геометрию системы, т.е. показывает, из каких элементов состоит САР и как эти элементы связаны между собой. Состояние САР, а также каждого входящего в нее элемента характеризуется некоторым числом независимых переменных. Этими переменными могут быть как электрические величины (ток, напряжение, и т.д.), так и механические (скорость, угол поворота, перемещение и т.д.). Обычно, чтобы характеризовать состояние системы или ее элемента, выбирают одну обобщенную координату на входе системы или элемента (g(t)) и одну – на выходе (x(t)). В ряде случаев такое представление невозможно, так как система или ее элемент могут иметь несколько входных и выходных величин. В многомерных системах можно рассматривать векторные входную и выходную величины с размерностями, совпадающими соответственно с числом входных и выходных величин САР.

Составление и линеаризация дифференциальных уравнений элементов систем.

При составлении дифференциальных уравнений САР основной задачей является составление дифференциальных уравнений отдельных элементов системы. Уравнение отдельных элементов составляются на основе тех физических законов, которые характеризуют поведение элемента.

При составлении дифференциальных уравнений элементов САР следует стремиться возможно точнее описать поведение данного элемента. Однако сложность получаемых при этом уравнений затрудняет исследование свойств их решений. Поэтому при составлении дифференциальных уравнений необходимо стремиться к разумному компромиссу между возможно более полным описанием поведения элемента и возможностью обозрения и исследования полученных уравнений.

Если динамика элемента описывается линейным дифференциальным уравнением, то этот элемент называется линейным, если дифференциальное уравнение не линейно, то элемент называется нелинейным.

Для упрощения анализа, когда это возможно, приближенно заменяют нелинейные дифференциальные уравнения такими линейными уравнениями, решение которых с достаточной степенью точности совпадают с решениями нелинейных уравнений. Этот процесс замены нелинейного дифференциального уравнения линейным называется линеаризацией.

Если дифференциальное уравнение элемента нелинейно из-за нелинейности его статической характеристики, то линеаризация уравнения сводится к замене нелинейной характеристики элемента x=φ(g) некоторой линейной функцией x=ag+b. Аналитически эта замена производится с помощью разложения в ряд Тейлора функции x=φ(g) в окрестности точки, соответствующей установившемуся состоянию и отбрасывания всех членов содержащих отклонение ∆g входной величины элемента в степени выше первой. Геометрически это означает замену кривой x=φ(g) касательной, проведенной к кривой в точке (x₀, g₀), соответствующей установившемуся состоянию работы элемента (рис. 29). В других случаях линеаризация производится путем проведения секущей, мало отклоняющейся от функции x=φ(g) в требуемом диапазоне изменения входной величины элемента.

Наряду с линеаризуемыми характеристиками имеются такие характеристики, которые не поддаются такой линеаризации. К ним относятся, например, характеристики, не разлагаемые в ряд Тейлора в окрестности точки установившегося состояния. Такие характеристики будем называть существенно нелинейными.

Рассмотрим процесс линеаризации нелинейного уравнения элемента с помощью ряда Тейлора. Пусть поведение элемента описывается нелинейным дифференциальным уравнением

F(xⁿ, x^’, x, g) = 0 (1). Тогда установившееся состояние элемента характеризуется уравнением F(0, 0, x, g) = 0 (2). пусть g₀ и х₀ – значения установившегося состояния. Тогда координаты g и х можно записать в виде x = x₀ + ∆x, g = g₀ + ∆g, где ∆g и ∆x – отклонение координат g и х от установившегося состояния. Уравнение (1) в отклонениях имеет вид:

F(∆x^’’, ∆x^’, x₀ + ∆x, g₀ + ∆g) = 0 (3).

Разложим левую часть уравнения (3) в ряд Тейлора относительно точки установившегося состояния (0, 0, x₀, g₀):

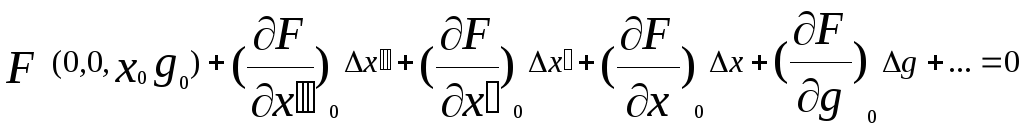(4).

Частные производные в левой части уравнения (4) представляют собой некоторые числа, величины которых зависят от вида функции F(x^’’, x^’, x, g) и значений координат x₀ и g₀.

Считая отклонения ∆g, ∆x от установившегося состояния, а также их производные по времени малыми и пологая, что функция F(x^’’, x^’, x, g) достаточно гладкая по всем аргументам в окрестности точки, соответствующей установившемуся состоянию, отбросим в уравнении (4) все члены, которые содержат отклонения ∆g и ∆x, а также их производные в степени выше первой. Полученное уравнение (5) является линейным дифференциальным уравнением с постоянными коэффициентами,,,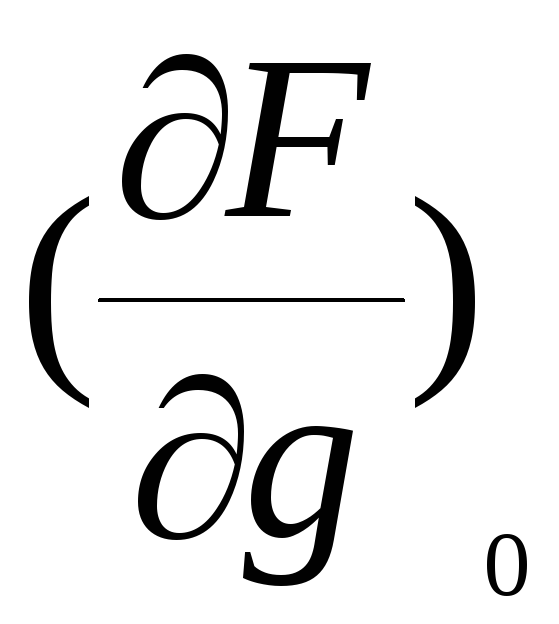и представляет собой результат линеаризации уравнения (1).

Очевидно, что необходимым условием линеаризации является возможность разложения в ряд Тейлора функции F(x^’’, x^’, x, g) в окрестности точки, соответствующей установившемуся состоянию.

Процесс линеаризации уравнения (1) может быть геометрически интерпретирован следующим образом. В пространстве переменных x^’’, x^’, x, g уравнение (1) задает некоторую поверхность. Переход от уравнения (1) к линейному уравнению (5) означает замену поверхности некоторой касательной плоскостью, проведенной к поверхности в точке, соответствующей установившемуся состоянию. Естественно, что ошибка при такой замене тем меньше, чем меньше отличаются друг от друга точки поверхности и точки плоскости. Это справедливо лишь в некоторой малой окрестности установившегося состояния.

Понятие управляемости и наблюдаемости.

Процесс или объект принято называть полностью управляемым, если он может быть переведен из некоторого состояния х(t₀) в желаемое состояние равновесия х(t₁) за конечный интервал времени t₁ – t₀. Другими словами, процесс является полностью управляемым, если существует управляющее воздействие m(t), определенное на конечном интервале времени t₀ ≤ t ≤ t₁, которое переводит процесс из начального состояния х(t₀) в желаемое состояние равновесия х(t₁) за время t₁ – t₀.

Необходимые и достаточные условия полной управляемости для случая дискретных систем можно сформулировать следующим образом.

Линейный дискретный процесс n-го порядка является полностью управляемым тогда и только тогда, когда векторы

s₁ = φ(-T)h(T),

s₂ = φ(-T)h(T),

…

s_n = φ(-T)h(T)

линейно независимы.

Эти векторы возникают в связи со следующими преобразованиями.

(t) = Ax(t) + d m(t),

в котором m(t) – единственное управляющее воздействие. Случай единственного управляющего воздействия рассматривается ради упрощения интерпретации получаемых выражений. Уравнение переходных состояний процесса имеет вид

,

где φ(Т) – матрица перехода процесса и .

Понятию управляемости можно дать еще и другое толкование, способствующее лучшему его пониманию. Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением (t) = Ax(t) + D m(t), где х – n-мерный вектор состояния;

m – r-мерный вектор, представляющий управляющие воздействия;

А – квадратичная матрица коэффициентов n-го порядка;

D – матрица управления размера n×r.

Матрица А может быть приведена к диагональной форме

,

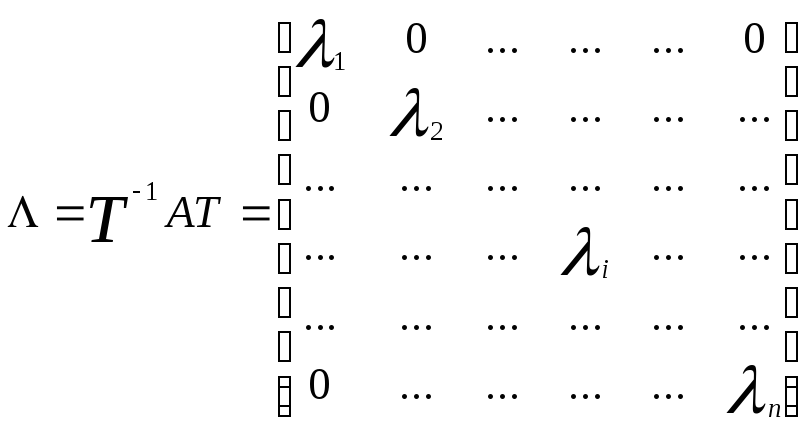где λ_i – собственные значения матрицы А линейного процесса, которые предполагаются все различными.

Применяя подстановку x=Tz, уравнение запишем в канонической форме

(t) = Λz(t) + ∆ m(t),

где . Векторz будем называть каноническим вектором состояния.

Процесс, описываемый уравнением (t) = Ax(t) + D m(t), является управляемым, если матрица ∆ не содержит строк, все элементы которых равны нулю; координаты, соответствующие ненулевым строкам ∆, считаются управляемыми.

Пример:

Вывести дифференциальное уравнение центробежного маятника, который применяется в качестве чувствительного элемента в некоторых САР. Схема маятника изображена на рисунке. Входной величиной является угловая скорость ω, а выходной величиной – перемещение х платформы. При увеличении скорости вращения шары под действием центробежной силы расходятся и перемещают платформу. На платформу воздействует также сила упругости пружины, силы демпфирования и силы инерции.

Введем обозначения: с – коэффициент жесткости пружины; k – коэффициент вязкого трения; m – масса шара; М – масса частей, участвующих в поступательном движении вдоль оси ОХ; ω – угловая скорость вала; f₀ – сила предварительного поджатия пружины.

Для составления дифференциального уравнения центробежного маятника используем уравнение Лагранжа второго рода: (I = 1, 2,…, n) (*). В качестве обобщенной координаты x_i выберем выходную координату – перемещение платформы х. Найдем выражение для кинетической энергии Т, потенциальной энергии П и диссипативной функции R центробежного маятника. Из рисунка видно, что

ρ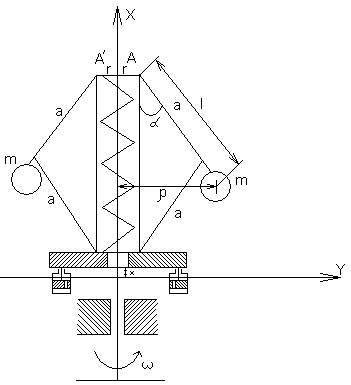 = r + l sin α, x = 2a(1 – cos α).

Кинетическая энергия системы Т = Т₁ + Т₂ + Т₃, где Т₁ – кинетическая энергия во вращательном движении вокруг оси ОХ; Т₂ – кинетическая энергия шаров во вращательном движении вокруг точек А и А’; Т₃ – кинетическая энергия масс в поступательном движении вдоль оси ОХ. Имеем:

,

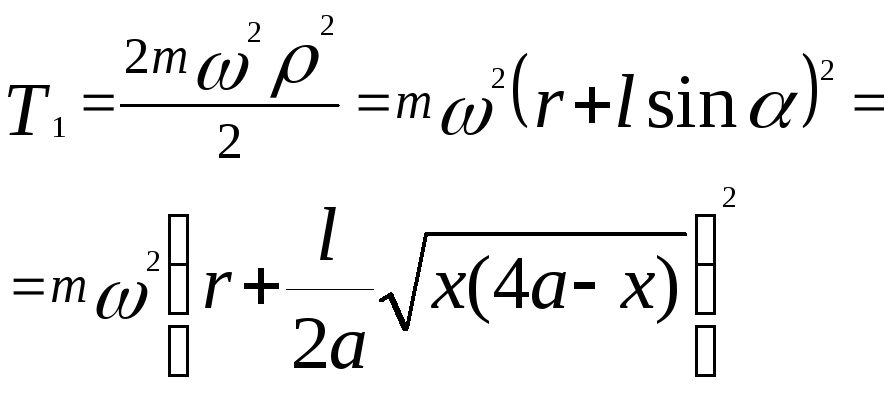, . (*1)

Потенциальная энергия маятника П = П₁ + П₂ + П₃, где П₁ – потенциальная энергия масс, движущихся параллельно оси ОХ; П₂ – потенциальная энергия; П₃ – потенциальная энергия пружины. Для рассматриваемого случая имеем:

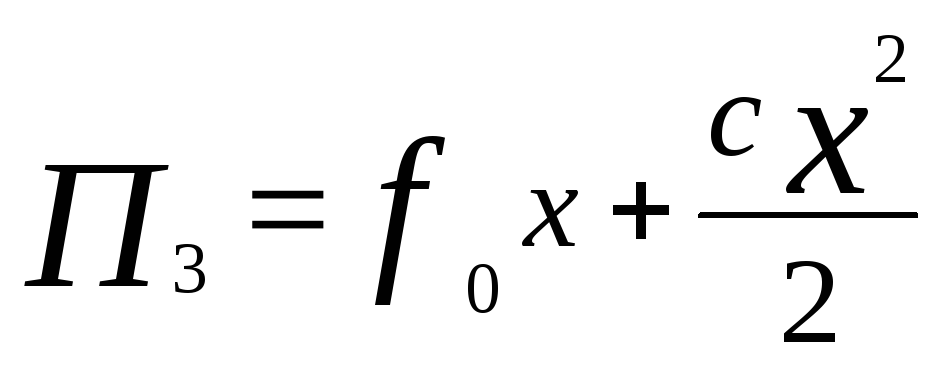, ,. (*2)

Найдем обобщенную диссипативную силу Q_R. Благодаря наличию демпфера сила сухого трения мала по сравнению с силой вязкого трения и ею можно пренебречь. Согласно формуле будем иметь

. (*3)

Вычислим значение отдельных слагаемых, входящих в уравнение Лагранжа (*):

,

,

,

.

Подставим полученные выражения в уравнение Лагранжа второго рода (*), тогда

или

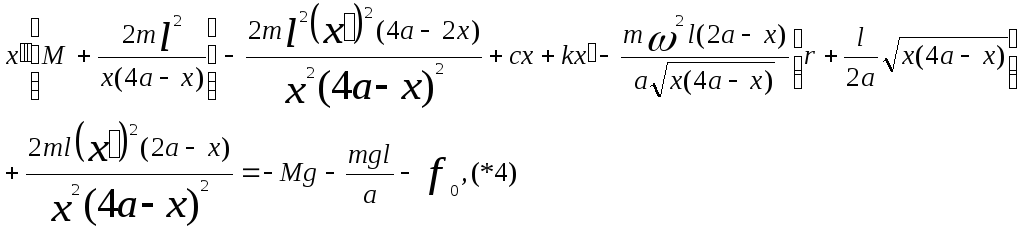
Введем следующее обозначения:

, ,

; (*5)

при r = 0

. (*6)

С учетом принятых обозначений уравнение центробежного маятника запишется в виде

. (*7)

Уравнение (*7) представляет собой нелинейное дифференциальное уравнение. Состояние равновесия (х₀, ω₀) является решением уравнения

. (*8)

Рассмотрим малые колебания маятника относительно состояния равновесия

(х₀, ω₀).

Положим

х = х₀ + ∆х, ω = ω₀ + ∆ω. (*9)

Разложим функции f₁(x), f₂(x), f₃(x, ω) в ряд Тейлора в окрестности состояния равновесия (х₀, ω₀).

(*10)

где функции F₁(∆x), F₂(∆x), F₃(∆x, ∆ω) имеют более высокий порядок малости по сравнению с ∆x и ∆ω. Учитывая, что x’ = ∆x’ и x” = ∆x”, и принимая во внимание выражения (*8), (*9), (*10), уравнение (*7) можно переписать в виде

где функция

имеет более высокий порядок малости по сравнению с . Отбрасывая функцию, получим линеаризованное уравнение колебаний маятника относительно состояния равновесия (х₀, ω₀)

, (*11)

где

,

(*12)

.