Основные свойства линейных разностных уравнений

Линейное разностное уравнение n-го порядка можно записать в форме:

(a_nEⁿ+a_n-lE^n-1 +... + a₁E + a₀)y(k) = F(k) (73)

где a_n≠0, a₀≠0 и а_i определены для всех интересующих нас целых значений k. В отличие от дифференциаль­ного уравнения, порядок разностного уравнения определяется как разность между высшей и низшей степенями Е. При использовании оператора ∆, например, в уравнении

[c_n∆ⁿ+c_n-1∆^n-1+...+c₁∆+c₀]y(k) = [d_m∆^m+...+d₁∆+d₀]v(k). (74)

установить порядок уравнения непосредственно по его виду не представля­ется возможным. Так, уравнение

(∆²+З∆+2)у(k)=0

эквивалентно

(E² + E)y(k) = 0,

являющемуся уравнением первого, а не второго порядка. Уравнение (73) называют неоднородным разностным уравнением, в отличие от однородного раз­ностного уравнения n-го порядка.

(a_nEⁿ+a_n-lE^n-1 +... + a₁E + a₀)y(k) = 0 (75)

Разностные уравнения называют также рекуррентными формулами. Уравне­ние (73) можно переписать в виде

y(k+n)=-1/a_n[a_n-1y(k + n-1) + ... + a₁y(k + 1) + a₀y(k) + F(k)] (76)

В отличие от дифференциальных уравнений, непосредственно по разност­ному уравнению можно определить y(k) для любых значений k; решение дается в виде первых n значений y(k) . Величины у(0) у(n-1) или эквивалентная информа­ция необходимы для единственности решения уравнения (73).

Однородное дифференциальное уравнение n-го порядка содержит n ли­нейно независимых решений. Если а_n≠0 и а₀≠0. то независимые уравнения (75) можно обозначить через y₁(k), y₂(k),...,y_n(k). Необходимое и достаточное ус­ловие линейной независимости решении имеет вид

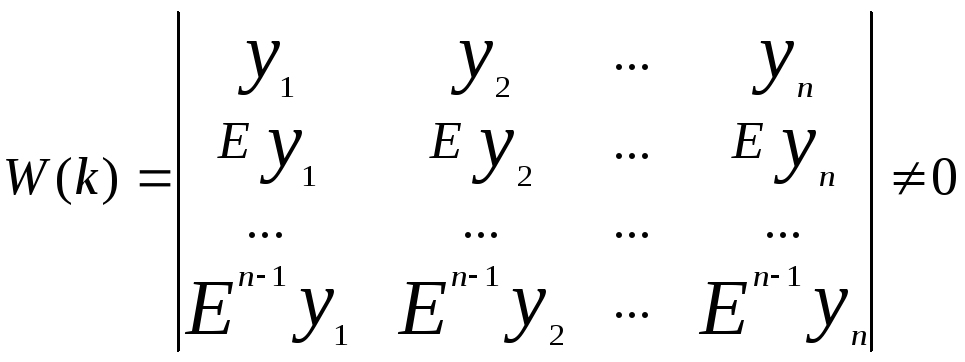(77)

В общем виде решение уравнения (75) представляется как

u_n=C₁y₁(k)+ C₂y₂(k)+ ...+C_ny_n(k), (78) где C_i -про­извольные постоянные не зависящие от k. Общее решение уравнения (73) имеет вид

y = y_н + y_p,

где у_н задается уравнением (78), а у_р - произвольное решение, удовлетворяющее уравнению (73). Составляющие у_н и у_р называют соответственно вспомогательным и частным решениями. Так как у_р не содержит произвольных постоянных, то в решении у содержатся n произвольных постоянных, которые должны определяться по начальным или граничным условиям.

Решение разностных уравнений с постоянными коэффициентами.

Для разностных уравнений с постоянными коэффициентами существуют детально разработанные методы нахождения решения в замкнутой форме. Неоднородное и однородное разностные уравнения n-го порядка задаются соответственно уравнениями (73) и

(75), где а_i постоянные коэффициенты.

Однородные разностные уравнения.

Рассмотрим уравнение n-го порядка

(a_nЕⁿ +а_n-1Е^n-1 + ... + а₁Е + a₀)y(k) = 0 (79)

Предлагаемое решение следует искать в виде

y(k)=e^rk, (80)

где r- подлежащая определению постоянная величина. Вид предполагаемого решения, задаваемый уравнением (80), не является наиболее распространенным. Допустимые значения r служат корнями многочлена от е^r. При β = е^r предполагаемое решение становится таким:

y(k)=β^k, (81)

где β - подлежащая определению постоянная величина. Подставляя уравнение (81) в (79) и учитывая E^mβ^k=β^mβ^k, получим следующее характеристическое уравнение:

а_nβⁿ+а_n-1β^n-1+... + а₁β + а₀ =0 (82)

Если n корней характеристического уравнения различны и обозначаются β₁, β₂,..., β_n, общее решение однородного разностного уравнения имеет вид

(83)

Неоднородные разностные уравнения. Метод неопределенных коэффициентов. Рассмотрим разностное уравнение n-го порядка

(a_nЕⁿ +а_n-1Е^n-1 + ... + а₁Е + a₀)y(k) = F(k), (84)

решение которого имеет вид:

y(k) = y_н + у_р . (85)

Вспомогательное решение у_н находится из решения соответ­ствующего однородного уравнения. Частное решение у_р находится на основе тех же самых двух методов, как и в случае дифференциальных уравнений, а именно: мето­дов неопределенных коэффициентов и вариации параметров. Метод неопре­деленных коэффициентов применим лишь в том случае, если в результате последовательного воздействия оператором Е на возмущающую функцию F(k) получаем конечное число линейно независимых членов. F(k) может быть много­членом, экспоненциальной, синусоидальной или гиперболической функцией или со­держать линейную комбинацию указанных функций. Решение ищут в виде ли­нейной комбинации составляющих F(k), F(k+1), F(k+2),..., причем каждая из составляющих входит с неопределенным постоянным коэффициентом.

Неоднородные разностные уравнения. Вариация параметров.

При известном решении вспомогательного уравнения метод ва­риации па­раметров позволяет получить выражение для у_р вне зависимости от характера функции F(k). Если применение этого метода к дифференциальным уравнениям сводится в конечном счете к интегрированию некоторой известной функции t, то применительно к разностным уравнениям приходим к суммированию неко­торой известной функции k. Рассмотрим уравнение первого порядка:

(a₁E + a₀)y(k) = F(k) (86)

Вспомогательное решение содержит лишь один член y_n=Cy₁(k).

Предполагаем, что частное решение имеет вид

У_р = μ(k)у₁. (87)

Подстановка уравнения (87) в (86) дает

a₁μ(k+1)у₁(k+1) + a₀μ(k)y₁(k) = F(k).

Преобразуем его к виду

a_l[μ(k+1)y₁(К+1)-μ(k)y₁(k+1)]+μ(k)[a₁y₁(k+1)+a₀y₁(k)]=F(k)

Выражение в первых скобках равно y₁(k+1)∆μ(k), а выражение во вторых скобках равно нулю, так как y₁(k) является решением соответствующего однородного уравнения. Следовательно, a₁y₁(k+1)∆μ(k)=F(k).

Рассмотрим разностное уравнение n-го порядка (84), вспомогательное решение кото­рого имеет вид

y_н=C₁y_l(k) + C₂y₂(k) + ... +C_ny_n(k).

Частное решение ищем в виде

y_p = μ₁(k)y₁(k) + μ₂(k)y₂(k) + ... + μ_n(k)y_n(k). (88)

Следующие n-1 условий выбираются произвольно с целью упрощения ре­шения:

y₁(k+1)∆μ₁(k) + y₂(k+1)∆μ2(k) +…+ y_n(k+1)∆μ₀(k) = 0,

y₁(k+2)∆μ₁(k) + y₂(k+2)∆μ2(k) +…+ y_n(k+2)∆μ₀(k) = 0,

…………………………………………………………......

y₁(k+n-1)∆μ₁(k) + y₂(k+n-1)∆μ₂(k) +…+ y_n(k+n-1)∆μ₀(k) = 0, (89)

Подставив уравнение (88) в уравнение (84) и используя (89), получим

y₁(k+n)∆μ₁(k) + y₂(k+n)∆μ₂(k) +…+ y_n(k+n)∆μ_n(k) = F(k)/a_n (90)

Получение импульсной характеристики на основе разностного уравнения.

Реакция на дельта-функцию (импульсная харак­теристика), обозначаемая че­рез d(k), представляет собой реакцию предварительно невозбужденной дис­кретной системы на сигнал

При рассмотрении раз­ностных уравнений масштаб времени предпо­лагается таким, что Т=1.