Решение дифференциальных уравнений с изменяющимися во времени коэффициентами.
Дифференциальное уравнение, описывающие нестационарную систему, задается в виде (1), (2), где коэффициенты аi и bi в данном случае являются функциями времени:
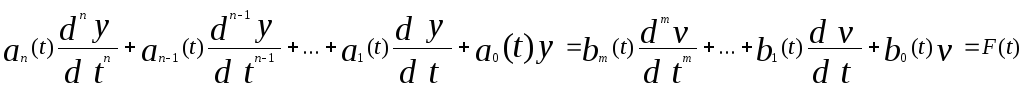(45)
А(р, t)y(t)=B(p, t)v(t)=F(t).
Вспомогательное решение.
Рассмотрим уравнение (45) при F(t)=0. Решение в виде у = ert, где r - постоянная величина, приводит к уравнению
аnrn +... + а1r + а0 =0.
Но так как в рассматриваемом случае аi являются функциями времени, то и корпи этого уравнения также являются функциями времени, что противоречит сделанному предположению. Вообще не существует общего метода нахождения ун в виде элементарных функций. Иногда полезно знать, что если известны n-1 неизвестных решений однородного уравнения n-го порядка, то оставшееся решение находится путем модификации метода вариации параметров.
Если коэффициенты аi, являются полиномами от t, то решение можно получить в виде бесконечного ряда. Наглядными примерами служат уравнения Бесселя и Лежандра. В виде бесконечного ряда ищется решение и при дробно-рациональных коэффициентах (представляющих отношение двух полиномов). Однако в этом случае бесконечный ряд имеет ограниченную область сходимости; поэтому если решение определяется на неограниченном интервале времени, следует использовать множество различных рядов.
Частное решение.
В отличие от метода неопределенных коэффициентов, метод вариации параметров применим для дифференциальных уравнений с изменяющимися во времени коэффициентами. Все этапы нахождения производных (уравнения (29), (35), (37)) справедливы вне зависимости оттого, являются или не являются аi функциями времени. Таким образом, если известно ун, то всегда можно определить ур.
Для дифференциальных уравнений с изменяющимися во времени коэффициентами справедлива также трактовка вспомогательного и частного решений как свободного и вынужденного движений.
Получение импульсной характеристики на основе дифференциального уравнения.
Хотя импульсная характеристика в ряде случаев задается непосредственно, важно уметь определять ее по описывающему систему дифференциальному уравнению. Поэтому рассмотрим уравнение
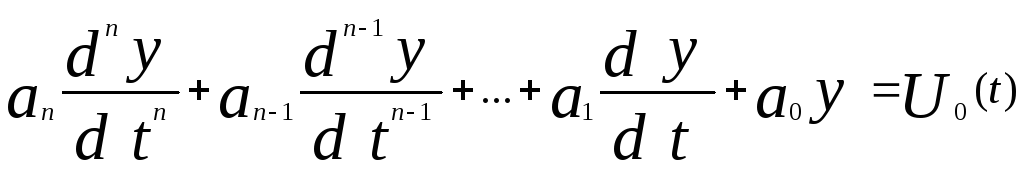(46)
Так как система не возбуждена при t < 0, то у= 0 при t<0. В связи с тем, что возмущающая функция U0(t) отлична от нуля лишь при t = 0, общее решение при t > 0 совпадает со вспомогательным решением
у=К1у1+К2у2+...+Кnуn (47)
Для вычисления n произвольных постоянных нужно знать n начальных условий. Для систем с постоянными параметрами, у которых коэффициенты аi - постоянные величины, начальные условия находятся непосредственно по этим коэффициентам. В момент времени t=0 n-я производная решения в отличие от производных низшего порядка содержит мгновенный импульс. Только в этом случае удовлетворяется уравнение (46) при t=0. Если одна из низших производных содержала бы мгновенный импульс, то dny/dtn содержала бы специальную функцию более высокого порядка. Так как в действительности an (dny/dtn) содержит единичный мгновенный импульс при t=0, dn-1y/dtn-1 должна претерпевать скачок от 0 до 1/аn в момент t=0, а все остальные производные в начальный момент должны быть непрерывными.
n -начальных условий должны иметь вид
y(0+)=
(0+)=...=yn-2(0+)=0,
yn-1(0+)=1/an
(48)
система с постоянными параметрами описывается уравнением (1)
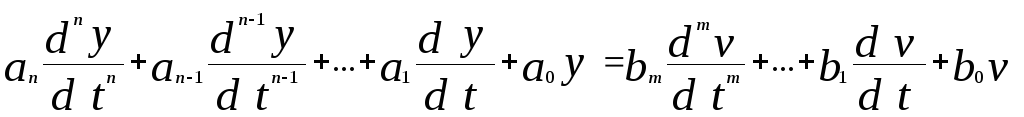(49)
A(p)y(t)=B(p)v(t)=F(t).
Если коэффициенты bi отличны от нуля, описанная выше процедура должна быть видоизменена. При v(t) =U0(t) правая часть уравнения (49) содержит специальные функции различного порядка. Один из удобных подходов предполагает, что для малых неотрицательных значений времени y(t) может быть разложена в ряд Тэйлора.
Импульсная характеристика нестационарных систем.
Изложенный выше подход нельзя непосредственно распространить на нестационарные системы, для которых операторы А и В являются функциями времени:
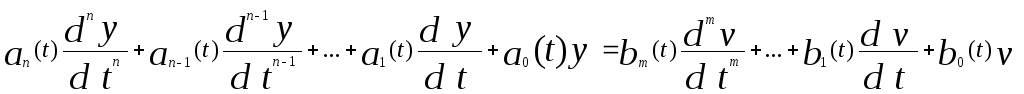(50)
A(p, t)y(t)=B(p, t)v(t)=F(t).
Как для стационарных, так и нестационарных систем справедлив метод, непосредственно связанный с уравнениями (41) - (44). Для систем без упреждения при равном нулю входном сигнале при t < 0 реакция на произвольный входной сигнал описывается уравнением:
(51)
Отметим сходство этого уравнения с уравнениями (42) - (44). Так как yi(t) не зависят от z, a F(z) и W(z) не зависят от i, уравнение (44) можно переписать в виде
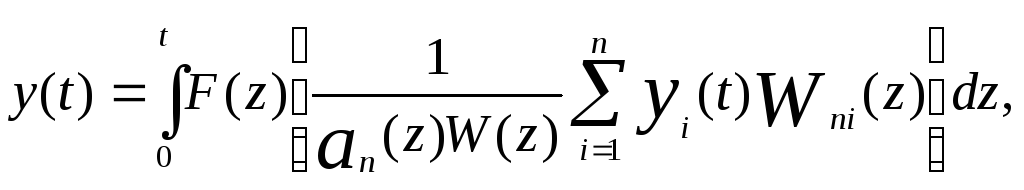(52)
где yi- n независимых решений однородного дифференциального уравнения. Выражение в скобках известно как однородная функция Грина.
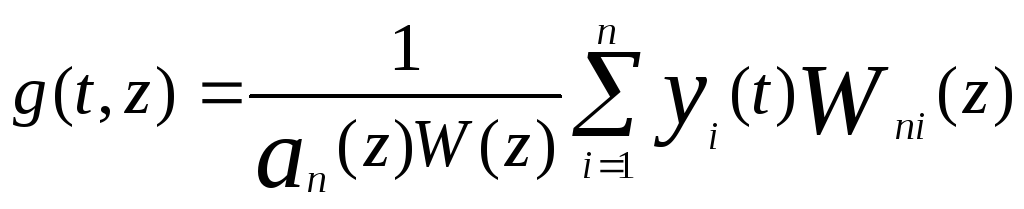(53)
Тогда
(54)
Прежде всего сравним уравнения (51) и (54) при F(t)=v(t), что соответствует
В(р, t)=1. Тогда
h(t, λ) = g(t, λ) при 0 < λ < 1,
h(t, λ) = 0 при t < λ.
Конечно, Wni(z)/an(z)W(z) соответствует в этом случае надлежащим значениям произвольных постоянных в импульсной характеристики. Функция Грина обладает рядом полезных свойств. Множители в уравнении (53) можно записать непосредственно в виде определителей на основе уравнения (38):
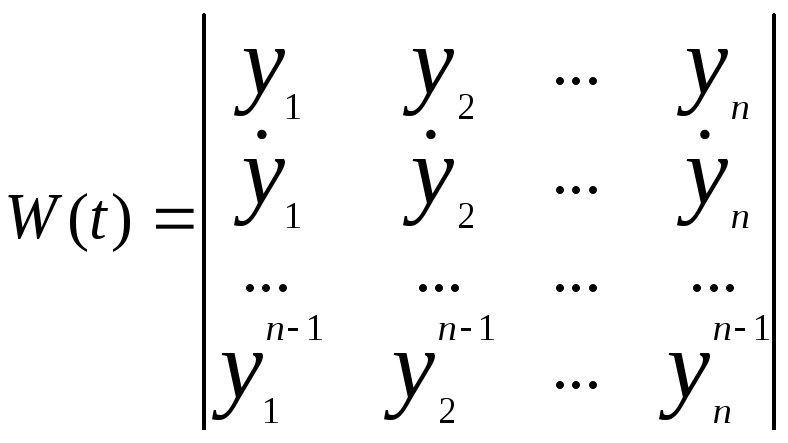(55)
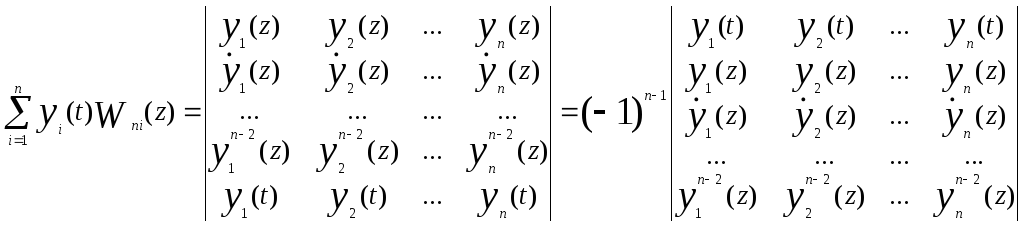
(56).
В общем случае F(t)≠v(t), и функция Грина не совпадает с импульсной характеристикой. Пусть теперь единственным ограничением в уравнении (50) будет m<n,
F(t)=B(p, t)v(t)=[ bm(t)pm+... + bl(t)p + b0(t)]v(t), (57)
где p — d/dt. Уравнение (54) можно использовать для определения импульсной характеристики при известной функции Грина.
Если v(t)=U0(t-λ), то y(t)=h(t, λ),
(58)
здесь р = d/dz. Уравнение (58) используется только для нахождения импульсной характеристики на интервале 0 <λ< t. При этом подынтегральное выражение отлично от нуля лишь при z=λ, в связи с чем пределы интегрирования можно изменить на -∞ и +∞. Данное уравнение не является настолько сложным, как это кажется на первый взгляд. Составляющие В(р, z) U0(z- λ) имеют вид:
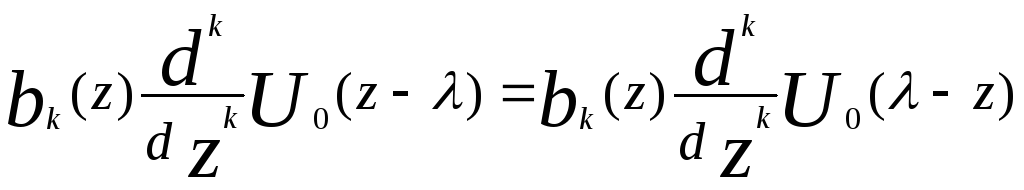
Таким образом, уравнение (53) позволяет получить h(t, λ)=g(t, λ) при 0<λ<t и F(t)= v(t). В этом случае h(t, λ) определяется согласно уравнению (58). Указанное уравнение составляет общий метод нахождения импульсной характеристики по линейному дифференциальному уравнению. Принципиальное ограничение состоит в том, что не существует общего метода для определения решений у1,..., уn однородного дифференциального уравнения с переменными коэффициентами.