Решение дифференциальных уравнений с постоянными коэффициентами

Линейные стационарные системы описываются линейными дифференци­альными уравнениями с постоянными коэффициентами. Однородное и неод­нородное уравнения n-го порядка задаются соответственно уравнениями (11) и (12), где а_i постоянные коэффициенты.

Однородные дифференциальные уравнения.

Рассмотрим уравнение n- го порядка

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y = 0. (19)

Предположим, что решение имеет вид y=e^rt, где г- подлежащая определению постоянная величина. Подставив предполагаемое решение в уравнение (19), получим

(a_nrⁿ + a_n-1r^n-1 +…+ a₁r + a₀)e^rt = 0. (20)

Так как это уравнение удовлетворяется при всех значениях t, то

a_nrⁿ + a_n-1r^n-1 +…+ a₁r + a₀ = 0. (21)

Уравнение (21) называют вспомогательным или характеристическим. Его можно записать не­посредственно из уравнения (19). В левой части (21) стоит полином n-го порядка, так что оно содержит n корней. Обозначим корни через r1; r2, ...,г_n. Тогда соответствующие решения уравнения (19) равен

y₁ = e^r1t, y₂ = e^r2t,…, y_n = e^rnt.

Если эти n ре­ше­ний ли­нейно неза­ви­симы, то об­щее ре­ше­ние одно­род­ного диф­фе­рен­ци­аль­ного урав­нения имеет вид

y_н = K₁e^r1t + K₂e^r2t +…+K_ne^rnt. (22)

Если все корни г_i раз­ные, то из (13) сле­дует, что опре­дели­тель Врон­ского отли­чен от нуля и, та­ким обра­зом, n от­дель­ных ре­ше­ний неза­ви­симы. Если r₁ = r₂, то не­зави­симы реше­ния y₁ = e^r1t и y₂ = te^r2t. Если, на­при­мер, r₁ имеет крат­ность k, т.е. r₁ = r₂ =...= r_k то общее ре­ше­ние запи­сыва­ется в виде

y_н = K₁e^r1t + K₂te^r1t +…+ K_kt^k-1e^r1t + K_k+1te^r(k+1)t +…+K_ne^rnt (23)

Та­ким обра­зом, для на­хож­дения уⁿ тре­бу­ется только вы­чис­ление кор­ней урав­нения n-го по­рядка. В связи с тем, что неко­торые корни могут быть ком­плексными, ре­ше­ние урав­нения можно за­пи­сать в дру­гой форме.

По­скольку ко­эффи­ци­енты урав­нения (12) дейст­ви­тель­ные, ком­плексные корни должны быть ком­плексно со­пря­жен­ными. Так, если один из кор­ней равен r₁ = α+iβ, где α и β - дейст­ви­тель­ные вели­чины, то другой из кор­ней дол­жен быть r₂ = α-iβ. Тогда

K₁e^r1t + K₂e^r2t = e^αt(K₁e^iβt + K₂e^-iβt) = e^αt[(K₁ + K₂)cosβt + i(K₁ - K₂)sinβt] =

= e^αt[Acosβt + Bainβt].

В реальной системе а_i — действительные числа, а у_n — действительная функция времени. Поэтому произвольные постоянные А и В должны быть действительными числами, что в свою очередь означает, что К₁, и К₂ должны быть комплексно сопряженными. Учитывая, что два тригонометрических выражения одинаковой частоты можно свести к одному с фазовым углом, возможна также запись

K₁e^r1t + K₂e^r2t = Ke^αtcos(βt + φ).

Неоднородные дифференциальные уравнения.

Метод неопределенных коэффици­ентов. Рассмотрим уравнение

(a_npⁿ + a_n-1p^n-1 +…+ a₁p + a₀)y = F(t). (24)

решение которого имеет вид

y = y_н + y_p (25)

у_n определяется при F(t)=0 из решения соответствующего од­нородного уравнения, как ука­зано раньше. Существуют два стандартных метода нахождения частного решения у_р - ме­тод неопределенных коэффициентов и метод вариации параметров.

Метод неопределенных коэффициентов применяется в том случае, когда вы­нуждающая функция F(t) имеет конечное число линейно независимых производных. F(t) может быть многочленом целой положительной степени t или состоять из комбинации экспоненциальной, синусоидальной или гиперболической функций. При F(t), например, равной In t или , указанный метод неприменим (если не искать ре­шение в виде бесконечного ряда). В основе метода предполагается, что у представляет со­бой линейную комбинацию составляющих F(t) и их производных; при этом каж­дый элемент входит с неопределенным коэффициентом. Предполагаемое решение подставляется в уравнение (24).

Неопределенные коэффициенты выбираются таким образом, чтобы уравне­ние удовлетворялось при всех значениях t. В том случае, когда член F(t) в точности совладает по виду с какой-либо составляющей решения однородного уравне­ния, указанная процедура видоизменяется. В физике это сходно с явлением резонанса, когда система возбуждается на одной из ее собственных частот. Например, уравнение

для которого y_n=K₁e^-t+K₂e^-2t не удовлетворяется тождественно при у_р=А+Ве^-t вне зависимости от выбора А и В. Естественно, однако, предположить, что со­ставляющая решения, вызываемая возмущением указанного типа, должна затухать более медленно, чем при отсутствии возмущения. Поэтому ло­гично попытаться искать решение в виде

у_р=А+Вtе^-t

Подставляя это решение в дифференциальное уравнение, найдем, что оно удовлетворяется тождественно при А=1/2 и В= -1. Если отдельные члены F(t) совпа­дают по форме с членами у_н, то процедура решения предполагает в общем случае умно­жение на t соответствующих составляющих в определяемом у_р. Подобная схема сохраняется, когда член F(t) содержит дополнительно множитель tⁿ. Однако в том случае, если какой-либо член F(t) соответствует кратному корню характери­стического уравнения (например, корню m-го порядка), соответствующий член в у_р следует умножить на t^m. Пример: Найти общее решение уравнения

Характеристическое уравнение: г²+2г+1=0; отсюда r₁ = r₂ = -1 и y_н=K₁te^-t+К₂tе^-t. Хотя обычно у_р=Аtе^-t+Ве^-t, в данном примере характерис­тиче­ское урав­не­ние со­дер­жит два оди­нако­вых корня -1;

сле­дова­тельно, yp=At³e^-t+Bt²e^-t

Заме­тим, что хотя по­втор­ное диф­фе­рен­циро­вание At³e^-t также при­водит к вы­раже­ниям Cte^-t и De^-t эти выра­жения не вхо­дят в пред­пола­гае­мое ре­ше­ние у_р. Это объ­ясня­ется тем, что эти вы­ра­же­ния слу­жат ре­ше­ниями со­от­вет­ст­вую­щего одно­род­ного урав­нения и по­тому исчез­нут при под­ста­новке в ле­вую часть ис­ход­ного диф­фе­рен­ци­аль­ного уравнения. Под­ста­вив у_р, как ука­зано выше, полу­чим,

Сле­дова­тельно, А=1/6 , В=0, и, в ко­неч­ном счете, ре­ше­ние имеет вид

y=K₁te^-t+K₂e^-t+1/6t³e^-t.

Не­одно­род­ные диф­фе­рен­ци­аль­ные урав­нения. Ва­риа­ция па­ра­мет­ров.

В от­личие от ме­тода неоп­реде­лен­ных ко­эф­фи­циен­тов, метод на­хож­дения у_р по­сред­ством ва­риа­ции пара­мет­ров мо­жет при­ме­няться вне зави­симо­сти от­того, имеет или не имеет вы­нуж­даю­щая функ­ция F(t) ко­неч­ное число неза­виси­мых про­из­вод­ных. В от­личие от пер­вого ме­тода он при­ме­ним также и в том слу­чае, если коэф­фици­енты a_i в урав­нении (24) зави­сят от вре­мени. Ме­тод ва­риа­ции пара­мет­ров пред­пола­гает на­хож­дение част­ного ре­ше­ния на ос­нове со­став­ляю­щих ре­ше­ния одно­род­ного урав­нения.

(a₁p+a₀)y=F(t) (26)

Ре­ше­ние, удов­ле­тво­ряю­щее одно­род­ному диф­фе­рен­ци­аль­ному урав­не­нию

(а₁р+а₀)у=0 (27)

со­дер­жит один член у_н=Ку₁ Ча­стное ре­ше­ние ищем в виде y_p=uy₁ (28), где все три вели­чины явля­ются функ­циями вре­мени. Чтобы найти и, под­ста­вим урав­нение (28) в уравнение (26). Полу­чим

a₁(uy + uy₁) + a₀uy₁ = F(t),

где точки обо­зна­чают про­из­вод­ные по t. После пре­обра­зова­ний имеем

a₁uy₁ + u(a₁y₁ + a₀y₁) = F(t).

В по­след­нем урав­нении мно­жи­тель в скоб­ках равен нулю, так как y₁, удов­летво­ряет урав­нению (27). Сле­дова­тельно,

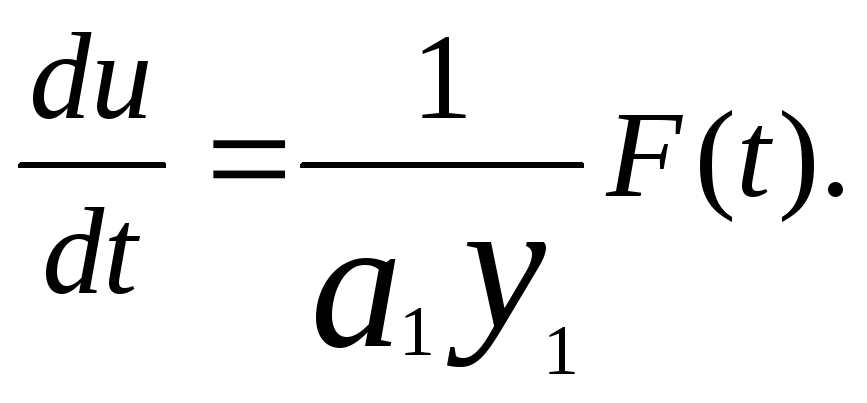(29)

Пример: Найти общее решение уравнения

Решение однородного уравнения у_н=Ке^-3t, т.е. y₁=e^-3t. Предполагая y_p=ue^-3t

u=ln t и y_p=e^-3tln t.

Общее решение имеет вид

y=Ke^-3t+e^-3tln t.

Рассмотрим дифференциальное уравнение второго порядка:

(a₂p²+a₁p+a₀)y=F(t) (30).

Решение удовлетворяющее однородному дифференциальному уравнению:

(a₂p²+a₁p+a₀)y=0 (31),

состоит из двух слагаемых: y_н=K₁y₁+K₂y₂

Частное решение ищем в виде

у_р= u₁y₁+u₂y₂ (32), где u₁ и u₂ являются неизвестными функциями времени. Для нахождения u₁ и u₂ тре­буются два условия. Одно из них состоит в том, что уравнение (32) должно удовлетво­рять уравнению (30). Другое условие можно выбрать любым наиболее выгод­ным образом

Выражения для ибудут менее громоздкими, если положить

u_ly₁+u₂y₂=0 (33)

Поэтому уравнение (33) становится вторым из двух необходимых условий:

Подстановка в уравнение (30) дает

Так как у₁ и у₂ удовлетворяют уравнению (31 ), то

u₁y₁+u₂y₂=F(t)/a₂ (34)

Чтобы получить в явном виде формулы для u₁ и u₂ необходимо решить совместно уравнения (33) и (34). Получим

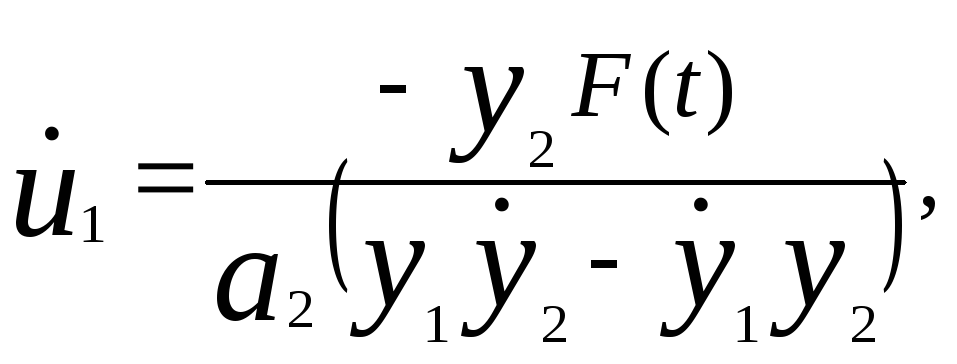
(35)

Следует отметить, что так как y₁ и у₂ - линейно независимые решения уравнения (31), то из (13) сле­дует, что y₁y₂-y₁y₂≠0 Так как знаменатель уравнения (35) отличен от нуля, u₁ и u₂ всегда существуют.

Рассмотрим дифференциальное уравнение n-го порядка типа

(a_npⁿ+a_n-1p^n-1+...+a₁p+a₀)y=F(t).

Решение однородного уравнения имеет вид

у_н=К₁у₁+К₂у₂+...+К_ny_n.

Частное решение ищем в виде

у_р= u₁y₁+u₂y₂+...+ u_ny_n. (36),

где u_i являются функциями t. Производные от u_i находим из совместного решения следующих n уравнений:

где точки и верхние индексы обозначают производные по t. Первые n-1 условий выбира­ются произвольно, с целью получения результата в обозримой форме. Последнее уравнение получено при подстановке предполагаемого решения у_р в уравнение (24) с учетом предыдущих n-1 условий.

Приведенная выше система уравнений решается на основе правила Крамера

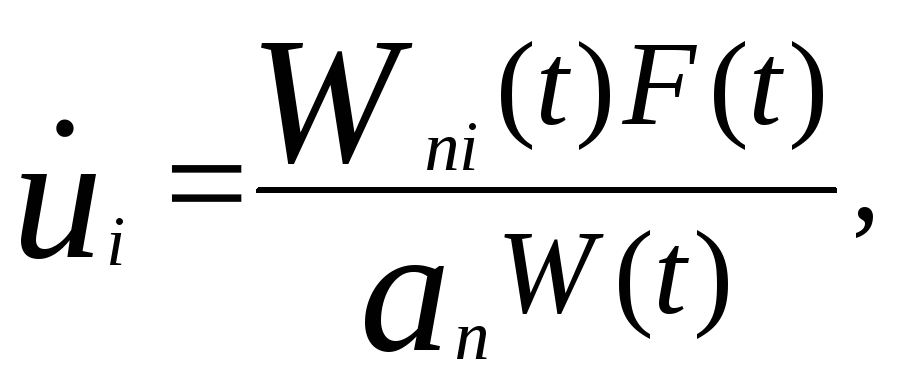i = (1, 2,…, n), (37)

где

, (38)

a Wni(t) - ni-e алгебраическое дополнение. Из (13) следует, что W(t)-определи­тель Вронского - отличен от нуля, если y₁, y₂,...,у_n -независимые решения од­нородного дифференциального уравнения.

Из сравнения двух стандартных методов нахождения у_р следует, что метод неопределенных коэффициентов зачастую проще. Недостатком его является, однако, то, что он справедлив лишь для ограниченного класса возмущающих функций и неприменим для систем с изменяющимися во времени парамет­рами. Метод вариации параметров позволяет всегда получить в явном виде выражение для у_р, если известно у_н. Решение дается а виде интеграла от из­вестной функции, в связи с чем у_р обычно называют частным интегральным решением. В ряде случаев непосредственное вычисление интеграла затруд­нительно и следует использовать численные методы. Существенным явля­ется то, что метод справедлив при любых вынуждающих функциях и может быть обобщен на системы с изменяющимися во времени коэффициентами.

Частное решение для входа e^st.

Общий вид системы с неиз­меняющимися во времени коэф­фициентами описывается уравнением (1). Вводя операторы А и В, получим

A(p)y(t)=B(p)v(t). (39)

Если v(t)=e^st, то частное решение имеет вид y_p(t)= H(s)e^st, где Н не зависит от t. Подстановка этих выражений в дифференциальное уравнение дает

A(p)[H(s)e^st]=B(p)[e^st].

Учитывая p^ke^st=s^ke^st, B(p)e^st=e^stB(s), где В - функция, образованная

заменой дифференциального оператора р на s, получаем

H(s)e^stA(s)=e^stB(s) или H(s)=B(s)/A(s). (40)

Следовательно, H(s) можно записать из дифференциального уравнения.

Н (s) обычно называют передаточной функцией системы. Воз­можность так легко определять ре­акцию на e^st позволяет исполь­зовать разложение произвольного входного сигнала в ряд по функциям e^st. Элементарной функцией является k(t, λ)=e^λt, а реакция на элементарную функцию, равна K(t, λ)= Н(λ)е^λt. Подобный подход приводит к преобразованию Лап­ласа.

Оди­нако­вые на­чаль­ные усло­вия.

В ряде важ­ных слу­чаев на­чаль­ные усло­вия оди­на­ковы. Для диф­фе­рен­ци­аль­ного урав­нения n-го по­рядка (24) оди­нако­вые на­чаль­ные усло­вия имеют вид

(41)

Ранее ис­поль­зуе­мый для на­хож­дения част­ного ре­ше­ния метод ва­риа­ции пара­мет­ров можно обобщить для полу­чения об­щего ре­ше­ния, удов­ле­тво­ряю­щего ука­зан­ным оди­нако­вым на­чаль­ным усло­виям. При n = 1 урав­нения (28) и (29) объе­диня­ются в

(42)

где у₁(t) - реше­ние одно­род­ного урав­нения, а z - фик­тив­ная пере­мен­ная ин­тег­риро­вания. Верхний пре­дел соот­вет­ст­вует рас­смот­рен­ному ранее част­ному ре­ше­нию, а ниж­ний пре­дел дает по­сто­ян­ную в ре­ше­нии одно­род­ного урав­нения. От­ме­тим, что у(0)=0. При n=2 урав­нения (32) и (35) объе­диня­ются в (43)

где y₁(t) и y₂(t) реше­ния одно­род­ного урав­нения, a W(t) — оп­реде­ли­тель Врон­ского,

W(t)=y₁(t)y₂(t)-y₁(t)y₂(t)

При­ве­ден­ные выше заме­чания о пре­делах ин­тег­риро­вания справед­ливы и в этом случае. От­метим, что у(0) = 0 и

Выражение в последней скобке всегда равно нулю, как следует из уравнения (33), так что соблюдается у(0)=0.

В общем случае дифференциального уравнения n-го порядка при одинаковых начальных условиях из уравнений (36) и (37) следует

(44)

где W(t) и W_ni(t) определяются уравнением (38). Так как основу рассуждений составляет метод вариации пара­метров, уравнения (41) и (44) справедливы как для систем с постоянными, так и с переменными параметрами. Данные уравнения применяются при нахождении импульсной характеристики нестационарной системы.

Физический смысл частного и вспомогательного решений.

Решение однородного уравнения (вспомогательное решение) зависит только от свойств системы и не зависит от входного воздействия. Характеристиче­ское уравнение зависит только от параметров системы, а корни характери­стического уравнения определяют вид составляющих вспомогательного ре­шения. В случае отсутствия внешних источников (т. е. система возбуждается запасенной в ней начальной энергией) вспомогательное решение совпадает с общим решением. Таким образом, вспомогательное решение характеризует «естественное» поведение системы при отсутствии внешних возмущений. В связи с этим вспомогательное решение называют также свободным или не ­вынужденными движением. Если вспомогательное решение системы неогра­ниченно возрастает при стремлении t к бесконечности, говорят, что система неустойчивая. Так как вспомогательное решение содержит экс­поненциаль­ные члены, то система станет неустойчивой, если ее характеристическое уравнение содержит корень с положительной действительной частью. С дру­гой стороны, корни с отрицательной действительной частью обусловливают стремление к нулю составляющих решения при стремлении t к бесконечности. При рассмотрении корней характеристического уравнения в комплексной плоскости можно сформулировать следующее утверждение. Если система устойчива, то ее корни должны лежать в левой полуплоскости, а на мнимой оси могут находиться только простые корни.

Если все корни характеристического уравнения лежат в левой полуплоскости, то вспомогательное решение стремится к нулю при стремлении t к бесконеч­ности и «совпадает» с переходным процессом в системе.

Величины составляющих во вспомогательном решении, т. е. произвольные постоянные решения, зависят от двух факторов, одним из которых является входной сигнал. Другим фактором служит предыстория системы (до момента приложения входного сигнала), которая полностью определяется знанием запасенной в системе энергии к моменту приложения входного воздействия. Вид частного решения обусловливается вынуждающей функцией; его легко усмотреть из метода неопределенных коэффициентов. Время влияет на вид решения лишь в том случае, если составляющая вынужденной функции сов­падает с каким-либо членом в у_н. Так как в этом случае система возбуждается на одной из ее собственных частот, то подобное явление называют резонан­сом.

В связи с тем, что вид част­ного ре­ше­ния зави­сит от вход­ного воз­дей­ствия, его назы­вают также вы­нуж­ден­ным дви­же­нием. Если все корни ха­рак­тери­сти­че­ского урав­нения лежат в ле­вой полу­плос­кости, вы­нуж­ден­ное ре­ше­ние сов­па­дает с уста­но­вив­шимся дви­же­нием. Ве­ли­чины вы­нуж­ден­ных со­став­ляю­щих зави­сят как от пара­мет­ров сис­темы, так и от вход­ного сиг­нала.

Обычно счи­тают, что вы­нуж­ден­ная со­став­ляю­щая ре­ше­ния уста­нав­лива­ется мгно­венно при по­даче вход­ного сиг­нала. Сво­бод­ная же со­став­ляю­щая, т. е. вспо­мога­тель­ное ре­ше­ние, как бы на­страивает себя путем пра­виль­ного опре­деле­ния про­из­воль­ных по­сто­ян­ных, чтобы обес­пе­чить над­ле­жа­щий пере­ход сис­темы из не­воз­буж­ден­ного со­стоя­ния в со­стоя­ние, под­чи­нен­ное вход­ному воз­дей­ствию.

Неко­торые склонны рас­смат­ри­вать вспо­мога­тель­ное ре­ше­ние как пер­вона­чаль­ное со­про­тив­ление сис­темы жела­ниям входа. Ве­ли­чины про­из­воль­ных по­сто­ян­ных зави­сят от того, на­сколько ха­рак­тер вход­ного воз­дей­ствия отли­ча­ется от «ес­тест­вен­ного» пове­дения сис­темы.