7. Записывается результат измерения:

(19)

при заданном . Это означает, что с заданной доверительной вероятностью доверительный интервал накрывает , т.е. .

8. если необходимо, то находится относительная погрешность, при этом, поскольку Х₀ неизвестно, приближенно его заменяют на :

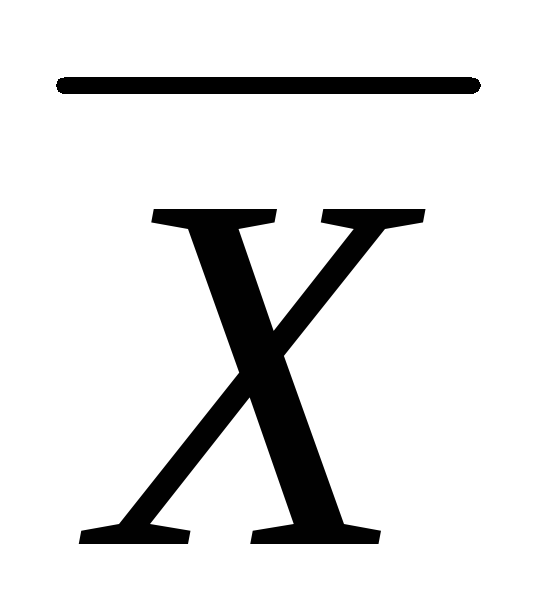. (20)

Методика оценки случайных погрешностей косвенных измерений

Чаще всего интересующая нас величина Х непосредственно не измеряется. Вместо этого измеряются некоторые величины , а затем вычисляется искомая величина Х, которая является функцией указанных непосредственно измеренных величин:

(21)

Для каждой из величин мы находим, как было указано выше, наиболее вероятное значение, т.е. среднеарифметическое из измеренных значений; и оцениваем их погрешности – либо вычисляем их среднеквадратичные погрешности для случая многократных изменений, либо находим максимальные погрешности , в случае отсутствия разброса в значениях при многократных измерениях.

Т.к. каждая из величин - случайна, случайной будет и величина Х – как функция случайных аргументов. Тогда, очевидно, наиболее близким к истинному значению Х₀ искомой величины будет значение функции:

. (22)

Погрешность результата косвенных измерений зависит от погрешностей прямых измерений каждой из величин, входящих в эту формулу.

Для расчета абсолютной погрешности косвенного измерения при заданной доверительной вероятности следует использовать выражение (даем без вывода):

(23)

где - погрешности прямых измерений при заданной доверительной вероятности (одинаковой для ), - частные производные функции по переменным соответственно. Напомним, что частная производная функции нескольких переменных по одной из них, например, по u, является обычной производной функции f по u, только при этом другие переменные считаются постоянными параметрами. Все производные в формуле (23) вычисляются при значении

Для нахождения максимальной абсолютной погрешности используют формулу:

(24)

Окончательный результат измерений и вычислений записывается в виде

при заданной доверительной вероятности :

или , где - максимальная абсолютная погрешность.

При этом обязательно нужно указывать название характеризующей результат меры точности или ). Если необходимо, указывается и значение относительной погрешности

или (25)

Порядок обработки результатов косвенных измерений следующий:

1. находятся средние арифметические и абсолютные погрешности по заданной доверительной вероятности и объему выборки для каждой величины по методике оценки случайной погрешности прямых измерений, приведенной в 4. При этом вероятность должна быть одинаковой для всех , а объем выборки может быть для них различным.

2. находится среднее значение результата косвенных измерений по формуле (22).

3. находится абсолютная погрешность косвенного измерения по формуле (23).

4. записывается результат измерения: