Методика вычислений инструментальных погрешностей прямых (непосредственных) измерений

Прямыми называются измерения, при которых результат измерения получается путем непосредственного сравнения измерения величины с эталоном или его эквивалентом, принятым за единицу измерения. X=n·[x],

где n – число, целое или дробное, [x] – единица измерения.

Погрешность измерения, выраженная в единицах измеряемой величины называется абсолютной погрешностью ∆X; численно она равна разности между результатом измерения Х и истинным значением Х₀ измеряемой величины:

∆Х = Х - Х₀. (1)

Если абсолютная погрешность по модулю не превышает некоторого положительного числа ∆X_м, то это число называется максимальной абсолютной погрешностью:

|Х – Х₀| = |∆Х |≤ ∆X_м . (2)

Относительной погрешностью называется отношение абсолютной погрешности к истинному значению измеряемой величины:

. (3)

Аналогично максимальная относительная погрешность равна отношению максимальной абсолютной погрешности к истинному значению измеряемой величины:

. (4)

Точность измерительных инструментов, приборов принято оценивать величиной приведенной погрешности, равной отношению максимальной абсолютной погрешности к верхнему пределу измерения для данного прибора (к пределу шкалы X_м):

. (5)

Приведенная погрешность, выраженная в процентах, называется классом точности прибора. Всего ГОСТом установлено восемь классов точности для измерения электрических величин: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности проставляется по шкале прибора. По известному классу точности можно найти максимальную абсолютную погрешность отдельного измерения:

. (6)

Например, вольтметр с классом точности 1,0 и шкалой до 30 В измеряет приложенное к нему напряжение с максимальной абсолютной погрешностью:

.

Это означает, что если результат измерения, например, 15,2 В, то истинное значение отличается от 15,2 В не больше, чем на 0,3 В, т.е.

или в другой записи .

Если на приборе не указан класс точности, то его максимальная абсолютная погрешность принимается равной половине цены деления шкалы. В некоторых случаях, например, при измерении времени секундомером, за величину максимальной абсолютной погрешности принимается целое деление (например, 0,02 с). В приборах с выдачей результатов измерения непосредственно на цифровом индикаторе за максимальную погрешность часто принимается единица младшего разряда.

В общем случае результаты прямых измерений содержат систематические, случайные и грубые погрешности. Систематические погрешности могут быть устранены либо в процессе измерения, либо учтены введением поправок в результаты. Поэтому условимся считать, что результаты прямых измерений содержат только случайные и грубые погрешности.

Методика оценки случайных погрешностей прямых равноточных измерений

Измерения называются равноточными, если они проведены одинаковыми по точности методами, или одним и тем же методом в одинаковых условиях. В результате n измерений некоторой физической величины x, истинное значение которой X₀ неизвестно, вследствие наличия случайных погрешностей получается ряд численных значений x₁; x₂, … , x_n, которые в общем случае отличаются друг от друга и от X₀.

При обработке результатов этих измерений возникают две задачи:

1. Нахождение по результатам отдельных измерений наилучшей оценки истинного значения, т.е. значения, наиболее близкого к истинному;

2. Определение погрешности полученной оценки.

Для большого числа практических случаев, когда грубые погрешности (промахи) встречаются редко, а случайные погрешности распределены по нормальному закону, наилучшей оценкой измеряемой величины является среднее арифметическое отдельных результатов измерения:

(7)

Отдельные результаты измерений являются случайными величинами, поскольку содержат случайные погрешности ∆Х_i:

∆х_i = х_i – х₀

Среднее арифметическое также является случайной величиной, как функция случайных величин. Поэтому абсолютная погрешность среднего арифметического, равная:

также будет случайной.

Это говорит о том, что истинное значение абсолютной погрешности найти невозможно, можно лишь тем или иным способом приближенно оценить ее значение. Например, можно считать, что с определенной вероятностью значение абсолютной погрешности по абсолютной величине будет меньше некоторой заданной величины , т.е.

. (8)

Отсюда следует, что истинное значение измеряемой величины с вероятностью накрывается интервалом , т.е.

. (9)

Интервал называется доверительным, а вероятность - доверительной вероятностью. Очевидно, чем больше - ширина доверительного интервала, тем с большей вероятностью доверительный интервал заключает в себе Х₀.

Таким образом, для характеристики случайной погрешности необходимо знать два числа, а именно – величину оценки абсолютной погрешности , которую часто называют просто абсолютной погрешностью, и величину доверительной вероятности.

В качестве ширины доверительного интервала можно взять

- среднеквадратичную погрешность или ее оценку S_x. Для отдельного измерения она равна:

. (10)

Среднее арифметическое имеет меньшее рассеивание и соответственно его среднеквадратичная погрешность будет меньше в раз.

. (11)

В физических, биологических, медицинских, физиологических и др. измерениях обычно пользуются значениями доверительной вероятности = 0,9; = 0,95; =0,99. При заданной доверительной вероятности ширину доверительного интервала (оценку погрешности) удобно находить в виде долей, т.е.:

, (12)

где - коэффициент, зависящий от величины доверительный вероятности и от объема выборки n. При интервал находится по таблице Стьюдента, при n> 30 он очень мало отличается от таблицы нормального распределения и в этом случае может быть найден по той же таблице при n= ∞.

Если взять величину абсолютной погрешности , то вероятность того, что доверительный интервал содержит Х₀ будет равна = 0,997. Это очень большая вероятность и поэтому говорят, что с практической уверенностью можно утверждать, что отклонение от Х₀ больше чем на невозможно. Это правило известно под названием “правила трех сигм”.

Наряду со среднеквадратичной погрешностью для оценки случайной погрешности пользуются и среднеарифметической погрешностью r, вычисленной по формуле:

. (13)

Все приведенные выше результаты теории случайных погрешностей применимы для характеристики точности измерения лишь в случае, если измерение многократно повторено.

Последовательность действий при оценке истинного значения измеряемой величины и оценки случайной погрешности следующая:

1. находится среднее арифметическое по результатам измерений:

, (14)

2. находится оценка среднеквадратической погрешности отдельного результата измерения:

, (15)

3. находится максимальная абсолютная погрешность отдельного измерения:

, (16)

4. проверяется, все ли результаты измерений укладываются в интервал 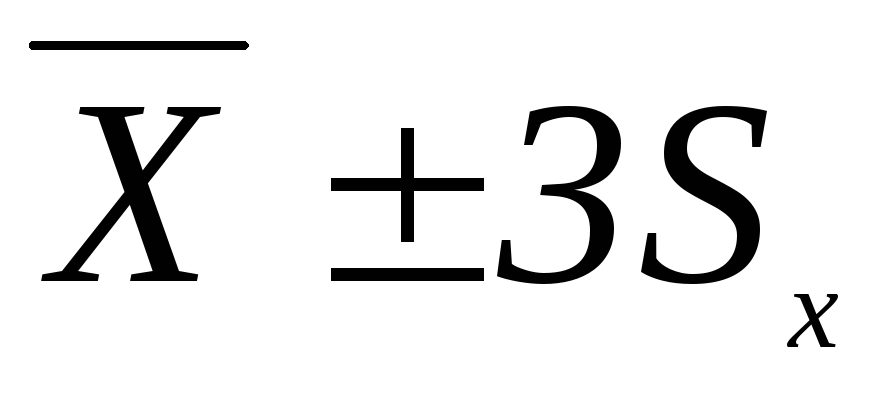, если да, то переходим к следующему пункту, если нет, то такое значение отбрасыватся (тем самым мы избавляемся от промахов) и вычисления следует начать сначала.

5. находится среднеквадратическая погрешность среднего арифметического:

(17)

6. находится из таблицы коэффициент 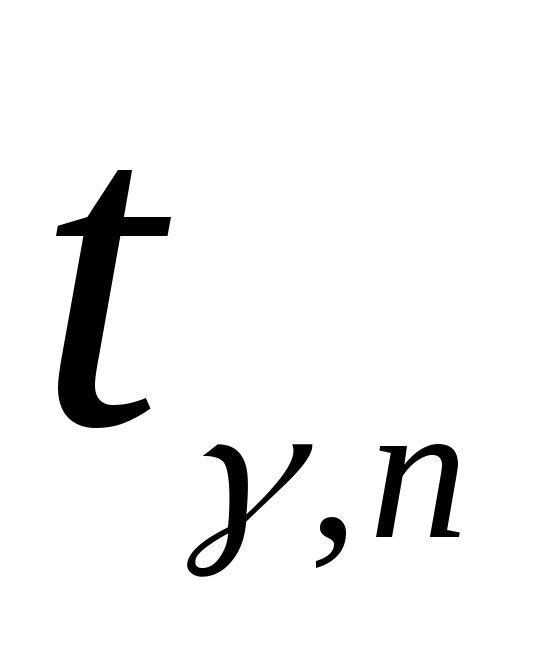по заданным и п и определяется оценка абсолютной погрешности:

(18)