0. Определенные и полуопределенные формы.

Квадратичная форма Q= <x,Ax> называетсяположительно определенной, если она не отрицательна при всех действительных значенияххи равна нулю тогда, когдах– нулевой вектор.

Квадратичная форма называется положительно полуопределенной, если она не отрицательна, может быть равна нулю, при отличном от нуля векторех.

Условия, удовлетворяющие этим формам:

		Ранг и индекс	Характеристические числа	А	Форма	Главные миноры
Положительно определенная
Действит. квадратич. форма. Эрнитовы форма	>0	r = p = n	λi>0	А = СтС ׀С׀>0 А = С*т С ׀С׀>0	Q = y12 + y22 +…+ yn2 Q = z1*z1 + z2*z2 + …+ zn*zn	∆1, ∆2,…, ∆n все «+» - С
Положительно полуопределенная
Действит. квадратич. форма. Эрнитовы форма	=0	r = p < n	n – rкорней равно 0, остальные положительные.	А = СтС ׀С׀ = 0 А = С*т С ׀С׀ = 0	Q = y12 + y22 +…+ yn2 Q = z1*z1 + z2*z2 + …+ zn*zn	∆1, ∆2,…, ∆n все «+» - С ∆
Отрицательно определенная
Действит. квадратич. форма. Эрнитовы форма		r = n p = 0	λi>0	А = -СтС ׀С׀>0 А = -С*т С ׀С׀>0	Q = -y12 - y22 -…-yn2 Q = -z1*z1 - z2*z2 - …- zn*zn	-∆1, +∆2,…, (-1)n ∆n все «+» - С
Отрицательно полуопределенная
Действит. квадратич. форма. Эрнитовы форма		r < n p = 0	n – rкорней равно 0, остальные отрицательны	А = -СтС ׀С׀ = 0 А = -С*т С ׀С׀ = 0	Q = -y12 - y22 -…-yn2 Q = -z1*z1 - z2*z2 - …- zn*zn	-∆1, +∆2,…, (-1)n ∆n все «+» - С (-1)n ∆n+ (-1)n ∆n-1 не «+»

7. Матричные многочлены.

Степени матрицы.

A^kA^m = A^k+m

(A^k)^m = A^km

A⁰ = I_n

(A^-1)^m = A^-m

ЕслиA^m= В, где А – квадратная матрица, тоA– кореньm-той степени В.

Матричные многочлены.

N(x) =P_nxⁿ+P_n-1x^n-1+…+P₁x+P₀(х – скалярная переменная).

хзаменяем квадратной матрицей А, то:

N(A) = P_nAⁿ + P_n-1A^n-1 +…+ P₁A + P₀I_n.

Бесконечные ряды матриц.

Запишем:

S(A) = a₀I_n + a₁A + a₂A² +…+ a_nAⁿ +…= a_kA^k, тогда геометрический ряд:

G(A) = I + aA + a²A² +…= a_kA^k.

Экспоненциальная функция:

e^A = expA = I +

Синусоидальная функция:

sinA=A- .

Косинусоидальная функция:

cosA = I -.

Гиперболический синус:

shA = A +.

Гиперболический косинус:

chA = I +.

Теорема Кэли-Гамеильтона.

I₀= - действительная матрица (2×2) (аналогj=).

sin aI₀ = aI₀ + I₀ sha. Обобщим: А^р= МА^рМ^-1.

Если N(λ) – многочлен отλ вида:N(λ) =λⁿ + C₁ λ^n-1 +…+ C_n-1 λ + C_n, то

N(A) = Aⁿ + C₁A^n-1 +…+ C_n-1A + C_nI = MN(λ)M^-1 = MM^-1, где λ₁, λ₂,…, λ_n – не нули N(λ).

Если N(λ) = Р(λ₁), то N(λ₁) = N(λ₂) =…= N(λ_n) = 0 Р(А) = [0], где

Р(λ) = |λI –A| матрица А удовлетворяет своему характеристическому уравнению.

Теорема Сельвестра.

Если N(A) – матричный многочлен от А и если квадратная матрица А содержитnразличных характеристических чисел, то многочлен от А можно записать в виде:

, где

.

Согласно теореме Кэли-Гамильтона:

N(A)=a₁A^n-1 +a₂A^n-2+…+a_n-1A+a_nI(произвольный матричный многочленN(A)) запишется многочленом А с наивысшей степеньюn–1.

Теорема Сельвестра. Вырожденная форма.

Если модифицировать уравнение: N(A) =(в том случае, когда А содержит кратные характеристические числа), тогда она (модификация) будет называтьсявырожденной формой теоремы Сильвера.

Если характеристический корень имеет порядок S, то можно показать, чтоN(A), обусловленнаяIкорнем λ_i, равно:

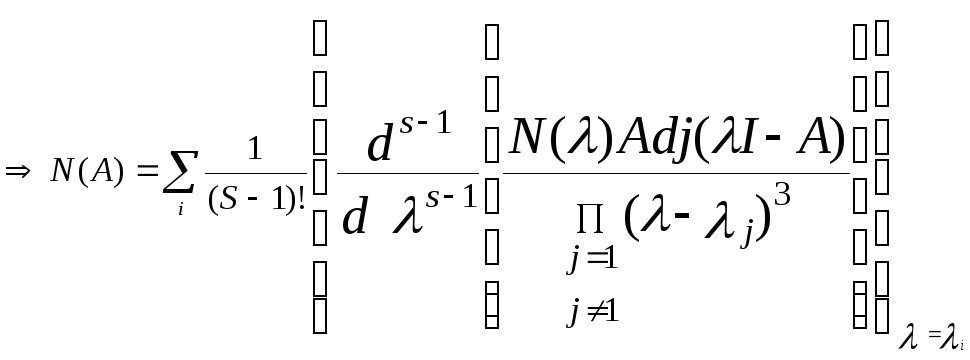
Метод Кэли-Гамильтона.

Рассмотрим случай, когда степень матричного многочлена N(A) выше, чем порядок А.

Делим N(λ) на характеристический многочлен А:

,R(λ) – остаточный член. Затем умножаем Р(λ):

N(λ) = Р(λ)Q(λ) + R(λ). Если Р(λ) = 0, тоN(λ) =R(λ). Т.к.P[A] = [0], то матричная функцияN(A) =R(A).

А если Q(λ) – аналитическая функция в области, тоF(λ) =Q(λ)Р(λ) +R(λ) (*), где Р(λ) – характеристический многочлен А, аR(λ) – многочлен вида:

Р(λ) = а₀+ а₁λ + а₂λ²+…+ а_n-1λ^n-1.

Т.к. Р(λ_i)=0, тоF(λ₁) =R(λ₁)

F(λ₂) =R(λ2)

…………….

F(λ₂) =R(λn)

Покажем, что - аналитическая функция λ. Нули знаменателя служат нулями и числителя, тоQ(λ) – аналитическая функция. Поэтому уравнение (*) справедливо для всех λ. Вместо λ можно подставить А:F(А) =Q(А)Р(А) +R(А). По теореме Кэли-Гамильтона: Р(А) = 0F(А) =R(А).