4. Характеристические числа и характеристические векторы.

От характеристических значений системы зависит ее динамические свойства.

у = А_х, гдеу их– векторы столбцы, а А – квадратная матрица (n×n).

у = А_х= λх, гдеλ– скалярный коэффициент пропорциональности.

Значение λ(λ_i), для которого уравнение у = А_химеет решениеx_i≠ 0 называетсяхарактеристическим числом А.Соответственный вектор решения x_i≠ 0 называетсяхарактеристическим вектором А.

4.1. Характеристическое уравнение.

Многочлен n-й степени относительно А, определенный уравнением, называетсяхарактеристическим уравнением А.

Р(λ) = λⁿ + a₁ λ^n-1 + a₂ λ^n-2 +…+ a_n-1 λ + a_n = 0. Корни характеристического уравнения равны характеристическим значениям А.

4.2. Модальная матрица.

Для каждого из (n) характеристических чисел λ_i(i= 1, 2,…,n) матрицы А можно получить решением уравненияотносительно х. Векторых_i, представленные решением системы(i= 1, 2,…,n), является характеристический вектор А.k_i– произвольная скалярная величина – решение (уравнение однородное). Матрица, образованная векторами-столбцами k_iх_iназываетсямодальной матрицей.

Симметрические матрицы. Свойство заключается в том, что характеристические числа симметрической матрицы должны быть действительными.

4.3. Диагонализация квадратной матрицы.

Рассмотрим несобственную модальную матрицу М (М^-1). Решение уравненияв виде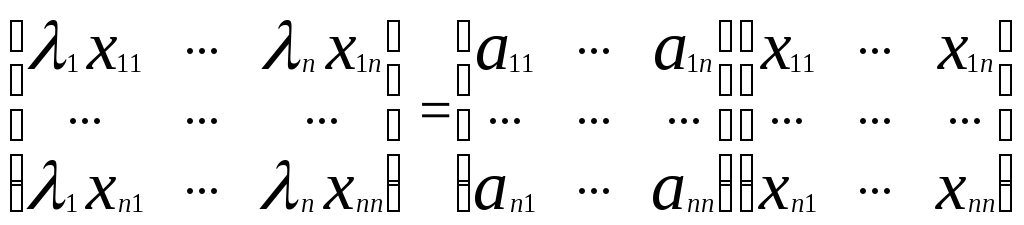или МΛ = АМ, где- диагональная матрица, состоящая из характеристических чиселλ₁,λ₂,…,λ_n.

Умножим обе части уравнения на М^-1: Λ = М^-1АМ. Более высокие степени матрицы А приводится к диагональному ряду так же. Преобразование вида В =Q^-1AQ, где А и В – квадратные матрицы,q– неособенная квадратная матрица, называетсяколлинеарным преобразованием илипреобразованием подобия.

5. Матричные преобразования.

Эквивалентные матрицы А и В считаются, если одна из матриц получается посредством выполнения ряда элементарных операций над другой. Матрица В эквивалентна матрице А, когда существуют такие две неособенные матрицы Р и Q, что В =PAQ.

Нормальная форма. Матрицу А ранга > 0 можно привести к эквивалентной матрице вида:I_r, ,или, гдеI_r– единичная матрица (r×r).

Данный вид называется нормальнойиликанонической формой матриц. Если А приводится к единичной матрице посредством ряда элементарных операций, то

А = Р^-1РАQQ^-1= Р^-1IQ^-1=P^-1Q^-1

Преобразование В = РАQ– общий вид матричного преобразования. Отдельные преобразования определяются из взаимосвязиPиQ. В частности преобразование подобия: В =Q^-1АQили Р =Q^-1.

Ортогональное преобразование.

В = Q^тАQ=Q^-1АQили Р =Q^т=Q^-1преобразование: В =Q^тАQили Р =Q^т.

Для эрнитовой матрицы А определяются:

а) коньютивное: В =Q^*ТАQили Р =Q^*Т.

б) унитарное: В =Q^*ТАQ=Q^-1АQили Р =Q^*Т=Q^-1.

6. Билинейная и квадратичная формы.

Билинейной формойотносительно переломныхх_i,у_i, называется выражение вида:

В = a₁₁x₁y₁+a₁₂x₁y₂+…+a_1nx₁y_n+a₂₁x₂y₁+a₂₂x₂y₂+…+a_2nx₂y_n+…+a_n1x_ny₁+…+a_nnx_ny_n, где все составляющие – действительные величины.

Комплексная форма: , или в матричной форме:

Матрица А – матрица коэффициентов формы, ранг А – ранг формы. Если х =у, то предыдущее уравнение превратится в:Q=x^TAx= <x,Ax>.

Qназываетсяквадратичной формойx₁,x₂,…,x_n. Или:.

Преобразование переменных.

Линейное преобразование х = Ву, где В – произвольная неособенная матрица (n×n), преобразуетQв квадратичную форму относительноу₁,у₂,…,у_n:Q=y^TB^TAByилиQ= у^тСу, где С = В^тАВ.