3. Векторы и линейные векторные пространства.

Скалярные произведение:

Для действительных хи узапишем как: <х, у> = х^т у = у^т х = <у, ч>.

Векторное произведение:

x><у = х(у^*)^т=, если вектор-столбецх(n×1) обозначить черезх>; вектор-строку (у^*)^т(1×m) – через<y.

Ортогональные вектора:

Единичные векторы.

Вектор называется единичным, если его длина равна единице так, что <> = 1.

Линейная зависимость.

Вектор х_i (i = 1, 2,…,m) с составляющимих_1i,х_2i,…,х_niназываютсялинейно независимыми, если не существует таких постоянныхk₁,k₂,…,k_m, что

k₁х₁+ k₂х₂+…+k_mх_m= 0.

Квадратная матрица называется особенной, если ее столбцы или строки не являются линейно-независимыми (, а если, то матрица неособенная). Если строки особенной матрицы линейно связаны одним соотношением, то матрица – просто вырожденная. Если более, чем одним соотношением, то – многократно вырожденной.

Рангом (r) матрицы (А) является наивысший порядок миноров матрицы А, отличных от нуля:r=n–g(n– порядок).

Определитель Грамма:

Система однородных уравнений имеет нетривиальное решение для k_iтолько в том случае, если определитель матрицы с коэффициентами [<x_i;x_j>] равен нулю. Этот определитель называетсяопределителем Грамаи равен:

система векторов линейно независимая тогда и только тогда, когда определитель Грама ≠ 0.

3.1. Линейное векторное пространство.

Наиболее простым примером линейного векторного пространства служит множество векторов, принадлежащих трехмерному пространству (эвклидову). Если система векторов х₁,х₂,…,х_mS, то и множество векторов (у), являющихся линейной комбинацией этих векторов, т.е. у =k₁х₁+ k₂х₂+…+k_mх_m, образующееся векторное пространство.

Базисом пространстваназывается такая система векторов, что произвольный вектор пространства выражается единственным образом в виде линейной комбинации этих векторов.

Если задана система, состоящая из mлинейно независимых векторов, то при помощи исходной системы векторов можно построить ортогональную систему изmлинейно независимых векторов. Если длина каждого вектора в ортогональной системе равна единице, то такая система называетсяортонормированной.

3.2. Решение линейных уравнений.

Правило Крамера.

Задана исходная система:

а₁₁х₁+а₁₂х₂+…+а_1nх_n=у₁

а₂₁х₁+а₂₂х₂+…+а_2nх_n=у₂

……………………………….

а_n1х₁+а_n2х₂+…+а_nnх_n=у_n

В более компактной форме: (i= 1, 2,…,n), или А_х= у, где,.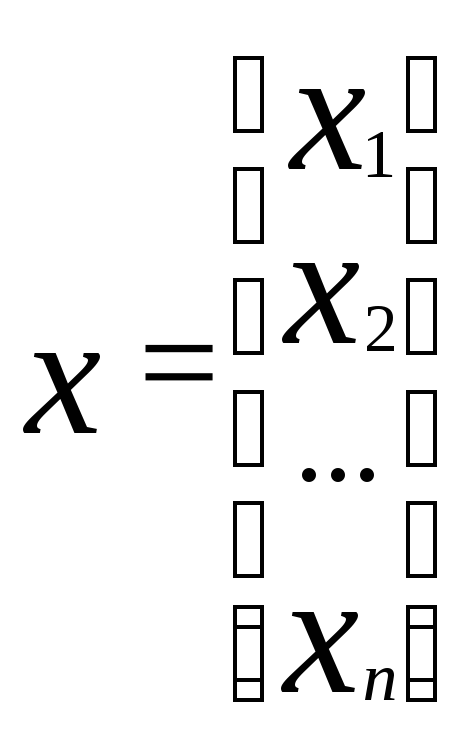

Итак, правило Крамера для построения решения при помощи определителей можно сформулировать следующим образом: система (n) линейных алгебраических уравнений с (n) неизвестнымих₁,х₂,…,х_n имеет решение, если матрица А несобственная.

Значение искомой переменной равно постоянному значению от деления двух определителей. Знаменатель равен определителю матрицы коэффициентов системы, а числитель равен определителю матрицы коэффициентов, k-й столбец в которой заменим столбцом, содержащие члены из правой части системы уравнений.

3.3. Однородная система линейных уравнений.

Если члены в правой части уравнения равны нулю, то система уравнений называется однородной.

Предположим, что ранг матрицы коэффициентов равен r.

1. Опускаем q = n – rуравнений так, чтобы определитель матрицы коэффициентов относительно rнеизвестных отличался от нуля.

2. Образуем rуравнений сrнеизвестными в левой части уравнения и оставшимся

q = n – rнеизвестными в правой части.r неизвестных выражается через q = n – rнеизвестных (qдеферент А).

Получаем qнезависимых решений в результате указанных этапов решения.