Исследование устойчивости по уравнениям первого приближения.

1. Уравнения первого приближения.

Пусть поведение системы автоматического регулирования описывается системой дифференциальных уравнений: . (38)

Пусть, кроме того, f(0)=0, т.е. начало координат х = 0 является состоянием равновесия. Исследование устойчивости любого состояния равновесия можно свести к этому случаю с помощью соответствующей замены переменных.

Будем полагать, что функции f_i(x₁,…,x_n) имеют непрерывные частные производные в некоторой области ║х║<μ. Разложим функции f_i(x₁,…,x_n), являющиеся компонентами вектор-функцииf(x), в ряд Тейлора в окрестности начала координат:

; (i= 1, 2,…,n), (39)

где , функциисодержат члены разложения порядка малости выше первого относительно переменныхx₁,…,x_nи поэтому:

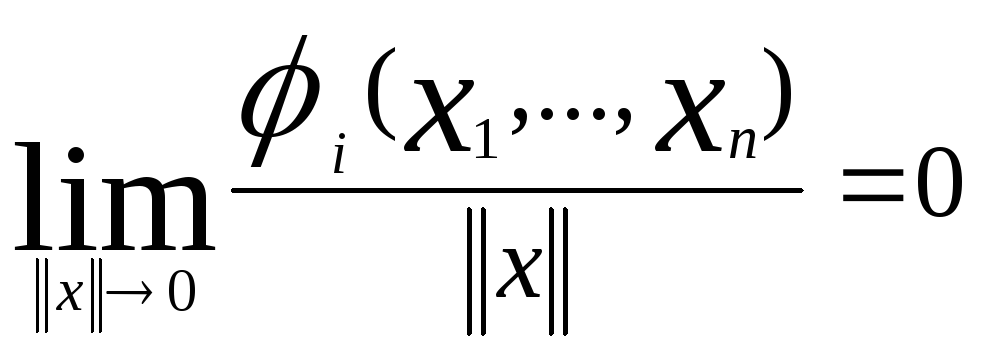. (40)

С учетом равенства (39) систему (38) можно переписать в виде: ,(41)

где А= [a_ij] – числовая матрица А;

φ(х) – вектор столбец, удовлетворяющий условию:. (42)

СЛДУ с постоянными коэффициентами: (43) называется системой первого приближения для (41), а значит и для системы (38).

2. Теорема Ляпунова об устойчивости в первом приближении.

Теорема 10:Тривиальное решение системы (41) автоматически устойчиво по Ляпунову, если все корни характеристического уравнения матрицы А системы (41) имеют отрицательные вещественные части, т.е.Reλ_i< 0 (i= 1, 2,…,n).

Теорема 11:Если среди корней характеристического уравнения матрицы А хотя бы один корень с положительной вещественной частью, то тривиальное решение системы (41) неустойчиво.

Исследование устойчивости нелинейных систем автоматического регулирования с помощью второго метода Ляпунова.

1. Уравнение нелинейных систем. Состояние равновесия.

Пусть нелинейная система автоматического регулирования состоит из линейного объекта регулирования и нелинейного регулятора. Поведение объекта регулирования описывается линейной системой дифференциальных уравнений с постоянными коэффициентами, которая в векторной записи имеет вид: , (44) где- вектор координат, характеризующих состояние объекта регулирования; у – скалярная координата, характеризующая воздействие регулятора на объект регулирования. Матрица А полагается невырожденной (detA≠ 0). Регулятор в своем составе имеет сервомеханизм, уравнение которого:

(45)

и чувствительный элемент, формирующий минор ошибки: ε=c^тх–rу, (46) гдеc^т=[c₁,..,c_n] – векторы постоянных коэффициентов;r – постоянный параметр обратной связи.

Относительно линейной функции f(ε) будем полагатьf(0)=0, εf(ε)>0, если ε≠0.

Функция f(ε) предполагается непрерывной при ε≠0, а в точке ε = 0 допускается разрыв непрерывности первого рода.

Система автоматического регулирования будет:

1. Собственно устойчива, если все корни характеристического уравнения out(A– λE) =0 имеют отрицательные вещественные частиReλ_i< 0.

2. Нейтральна по координатам x₁,…,x_n, еслиReλ₁=Reλ₂=…=Reλ_n= 0, а остальные корни характеристического уравнения существуют отрицательные вещественные части.

3. Собственно неустойчива, если хотя бы один корень характеристического уравнения имеет положительную вещественную часть.

2. Приведение уравнений движений к канонической форме.

Исследование устойчивости тривиального решения системы:

;;ε=c^тх–rу, (47)

удобно проводить, когда (47) приведена к каноническому виду. Канонической формой уравнений (47) назовем такой их вид, когда матрица А приведена к жордановой форме.

Сделаем в системе (47) замену переменных:

x=Tu(DecT≠0). (48)

Тогда система уравнений примет вид:

;;ε=c^тTu–rу,

или: ;;ε=u–rу, (49)

где В₁=Т^-1В;=c^тT.

Система (49) укрощается если выполнить еще раз замену:

,ε=u–rу. (50)

Тогда вместо системы (47) получим систему:

,. (51)

Система уравнений (51) является канонической формой уравнений движения.

3. Достаточные условия устойчивости состояния равновесия.

Исследуем устойчивость тривиального решения уравнения (51). Построим функцию Ляпунова, с помощью которой найдем условия накладываемые на параметры регулятора, при вынесении которых тривиальное решение (51) асимптотически устойчиво.

Рассмотрим случай, когда все корни характеристического уравнения простые и лежат в левой полуплоскости. Функцию Ляпунова будем искать в виде:

. (52)

Функция , определяемая выражением (52) будет определенно положительной, если квадратичная форма- положительно определена.

Составим полную производную от функции :

Учитывая, что матрица квадратичной формы является асимметрической В^т= В получим:

.

Введем в рассмотрение матрицу

с= -(j^TB+B_j). (53)

Т.о. полная производная функции может быть записана в виде:

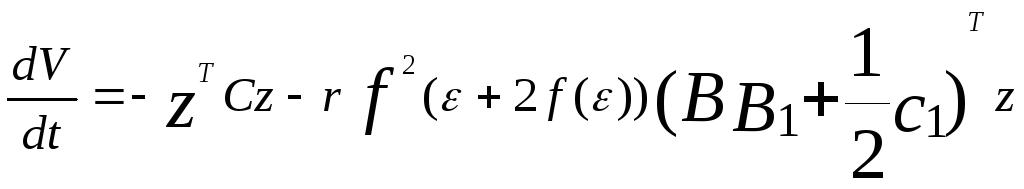. (54)

Если характеристические числа матрицы А заданной симметрической матрице С однозначно определяется симметрическая матрица В. Т.к. I=diagμ, то соотношение (53) можно представить в виде:c_ij= -(λ_iB_ij+λ_jB_ij)

откуда: . (55)

Теорема 12:Пусть матрица А устойчива, т.е. ее характеристические числа лежат в левой полуплоскости. Тогда, если с-матрица некоторой положительно определенной квадратичной формы, то определенная по формуле (55) матрица В также является матрицей положительно определенной квадратичной формы.