
- •3.8.3. Метод послідовних поступок
- •2.1. Поняття бінарного відношення
- •2.2. Способи задавання відношень
- •2.3. Операції над відношеннями
- •2.4. Властивості відношень
- •2.5. Відношення еквівалентності, порядку, домінування та переваги
- •2.6. Поняття r-оптимальності, найкращого, найгіршого, максимального та мінімального елементів
- •2.7. Поняття функції вибору. Класи функцій вибору
- •2.8. Функції корисності
- •Багатокритеріальні задачі оптимізації
- •3.1. Загальна постановка багатокритеріальної задачі оптимізації
- •3.2. Поняття ефективної альтернативи
- •3.3. Теоретичне і практичне значення ефективного рішення.
- •3.4. Властивості ефективних альтернатив і способи їх знаходження.
- •3.5. Загальна проблема пошуку компромісних рішень
- •3.5.1. Принципи рівномірності
- •3.5.2. Принципи справедливої поступки
- •3.5.3. Інші принципи оптимальності
- •3.6. Методи нормалізації критеріїв
- •3.7. Способи урахування пріоритету критеріїв
- •3.7.1. Методи урахування жорсткого пріоритету
- •3.7.2. Методи урахування гнучкого пріоритету
- •3.8. Методи розв’язання багатокритеріальних задач оптимізації
- •3.8.1. Методи зведення до узагальненого критерію (методи згортки)
- •3.8.2. Метод головного критерію
- •3.8.3. Метод послідовних поступок
2.6. Поняття r-оптимальності, найкращого, найгіршого, максимального та мінімального елементів
Приведені вище відомості були пов’язані з формалізацією попарного порівняння альтернатив, яка необхідна для виділення найкращого елемента (або декількох кращих) з всієї множини альтернатив Х. Для того ж щоб виділити «кращий» елемент необхідно формалізувати поняття «кращий». Використаємо для цього апарат бінарних відношень.
З обиранням за даним відношенням R кращого елемента тісно пов’язане поняття найкращого та найгіршого елементів.
Елемент
 з множини Х
будемо називати найкращим
за відношенням R,
якщо для
з множини Х
будемо називати найкращим
за відношенням R,
якщо для
 виконується
виконується
 .
.
Елемент
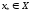 будемо називати найгіршим
за відношенням R,
якщо
будемо називати найгіршим
за відношенням R,
якщо
 має місце
має місце
 .
.
Легко бачити, що найкращій та найгірший елементи існують не завжди. Наприклад, їх не буде коли відношення не є повним. Розглянемо приклад.
П р и к л а д 2.12.
Нехай відношення R
подано на множині
 таким чином
таким чином
 .
.
Зобразимо це відношення за допомогою графа ( див. рис. 2.3)

Рис. 2.3. Граф відношення R (до прикладу 2.12)
Легко бачити, що це відношення не має найкращих та найгірших елементів, бо елементи а та с незрівняні. Уведемо поняття максимального елемента.
Елемент
 називається максимальним
за відношенням
називається максимальним
за відношенням
 на множині Х,
якщо для
на множині Х,
якщо для
 має місце або
має місце або
 ,
,
 або
або
 незрівняний з Х.
незрівняний з Х.
Тобто
не існує елемента (альтернативи)
 ,
який би був кращим за альтернативу
,
який би був кращим за альтернативу
 .
.
Елемент
 називається мінімальним
відносно R
на множині Х,
якщо для
називається мінімальним
відносно R
на множині Х,
якщо для
 або
або
 або х
незрівняний з
або х
незрівняний з
 .
Тобто не існує елемента
.
Тобто не існує елемента
 який би був гіршим за
який би був гіршим за
 ,
немає жодного елемента х,
який би домінувався елементом
,
немає жодного елемента х,
який би домінувався елементом
 .
.
У наведеному вище прикладі максимальним елементом буде елемент а, мінімальним – елемент с.
Множина
мінімальних за R
елементів
множини Х
позначається
 .
.
Зауважимо, що якщо найкращі елементи існують, то вони будуть і максимальними, але не навпаки.
Отже, якщо треба обрати найкращу в деякому сенсі альтернативу, то природнім буде її вибір із множини максимальних (недомінуємих) альтернатив.
П р и к л а д 2.13.
Нехай відношення R
подано графом G
(рис.
2.4). Знайти найкращі, найгірші, максимальні
та мінімальні за
 елементи.
елементи.

Рис. 2.4. Граф відношення R (до прикладу 2.13)
Розв’язування
Найкращих
елементів не має; найгірших елементів
також не має. Максимальними за
 є елементи а,
d,
e.
Мінімальними за
є елементи а,
d,
e.
Мінімальними за
 елементами будуть с,
d,
e.
елементами будуть с,
d,
e.
Позначимо
множину максимальних за R
об’єктів
множини X
як
 .
Ця множина внутрішньо
стійка
в тому сенсі, що якщо
.
Ця множина внутрішньо
стійка
в тому сенсі, що якщо
 ,
то не може бути ні
,
то не може бути ні
 ні
ні
 .
.
Множина
називається зовнішньо
стійкою,
якщо для кожного елемента
 ,
який не є максимальним, знайдеться
переважніший за нього елемент серед
максимальних. Тобто буде
,
який не є максимальним, знайдеться
переважніший за нього елемент серед
максимальних. Тобто буде
 для деякого
для деякого
 .
.
Внутрішнє
та зовнішнє стійка множина
 називається ядром
відношення R
в X.
Поняття стійкості має велике значення,
бо якщо множина
називається ядром
відношення R
в X.
Поняття стійкості має велике значення,
бо якщо множина
 зовнішньо стійка, то оптимальний елемент
повинен бути вибраний саме з цієї
множини. Якщо ж множина
зовнішньо стійка, то оптимальний елемент
повинен бути вибраний саме з цієї
множини. Якщо ж множина
 не є зовнішнє стійкою, то для обмеження
вибору цією множиною нема підстав.
не є зовнішнє стійкою, то для обмеження
вибору цією множиною нема підстав.
У випадку коли потрібно вибрати не один, а декілька кращих елементів, або впорядкувати всі об’єкти за перевагою, поняття максимального елемента і ядра втрачають своє значення.
П р и к л а д 2.14.
Нехай
 відношення
відношення
 Тут
Тут
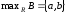 .
Однак, якщо потрібно вибрати два кращих
об’єкта, то відкидати c
не можна: якщо особа, що приймає рішення
повідомить, що с
переважніше,
ніж b,
то шуканими будуть елементи a
та
c.
.
Однак, якщо потрібно вибрати два кращих
об’єкта, то відкидати c
не можна: якщо особа, що приймає рішення
повідомить, що с
переважніше,
ніж b,
то шуканими будуть елементи a
та
c.
Числова
функція
 ,
яка визначена на множині Х
називається зростаючою
(не
спадною)
за відношенням R,
якщо з
,
яка визначена на множині Х
називається зростаючою
(не
спадною)
за відношенням R,
якщо з
 випливає
випливає
 (відповідно
(відповідно
 )
для всіх
)
для всіх
 .
.
Має місце така лема.
Лема
2.1. Нехай
 і
і
 надає не спадній за відношенням R
на В
функції Ψ
найбільше на В
значення. Для того щоб об’єкт
надає не спадній за відношенням R
на В
функції Ψ
найбільше на В
значення. Для того щоб об’єкт
 був максимальним за відношенням R
на В
достатньо
виконування однієї з наступних умов:
був максимальним за відношенням R
на В
достатньо
виконування однієї з наступних умов:
-
Ψ зростає за R на В.
-
 – єдина
точка максимуму Ψ
на В.
– єдина
точка максимуму Ψ
на В.
Доведення
Припустимо,
що
 не є максимальним за відношенням R.
Тоді в множині В
знайдеться такий елемент a,
що
не є максимальним за відношенням R.
Тоді в множині В
знайдеться такий елемент a,
що
 .
Але тоді повинно виконуватись
.
Але тоді повинно виконуватись
 ,
причому ця нерівність строга, якщо Ψ
зростає за R
на В.
Але строга нерівність суперечить тому,
що
,
причому ця нерівність строга, якщо Ψ
зростає за R
на В.
Але строга нерівність суперечить тому,
що
 точка максимуму Ψ,
нестрога нерівність – тому, що
точка максимуму Ψ,
нестрога нерівність – тому, що
 єдина точка максимуму Ψ
на В.
єдина точка максимуму Ψ
на В.
Доведення закінчено.
При моделюванні реальних систем можуть зустрітися такі ситуації, коли у ОПР, або у експертів нема чіткого уявлення про переваги між альтернативами. І якщо необхідно подати чіткі висновки про переваги, то в цьому випадку експерти повинні в певному сенсі “огрубляти” свої знання та уявлення, а математична модель буде менш адекватна реальній ситуації.
Більш
гнучким способом формалізації цих
уявлень є можливість для експертів
визначити міру свого переконання в
перевазі альтернативи числами з інтервалу
[0;1]. Тоді, за допомогою експертів,
формулюється нечітке
відношення переваги,
у якому кожній парі
 відповідає число з інтервалу [0,1], що
описує міру вірності переваги
відповідає число з інтервалу [0,1], що
описує міру вірності переваги
 .
Методи прийняття рішень на основі
нечітких відношень переваги буде
розглянуто далі в розділі 4.
.
Методи прийняття рішень на основі
нечітких відношень переваги буде
розглянуто далі в розділі 4.
Характерною особливістю «мови» бінарних відношень є припущення про те, що результат порівняння за перевагою двох елементів не залежить від складу всієї множини. Однак в ряді випадків така залежність має місце і для її врахування необхідна більш багата «мова» опису переваг, основана на використанні функцій вибору.
