
практическая работа / Математическое описание объектов или систем с помощью графов / вариант 17 (2)
.docxВариант №17
Задание № 1
Z’1=2Z1+0,5Z2+5Z3+Z4-6X;
Z’2=-0,5Z1-0,1Z2+0,5Z5;
Z’3=Z4-0,3Z5+0,1X+1,3Z3;
Z’4=-0,1Z4+Z5+0,1X+3,2Z3;
Z’5=9Z1+0,5Z2+0,6Z4-9Z5-0,6X;
Y=0,25Z1+0,1Z2+Z5;
В начале работы избовляемся от дифференциалов в заданной системе уравнений , для этого переходят к операторному виду , то есть производят замену оператору дифференцирования на оператор Лапласа . После этого строят граф , причем константа , которая находится при операторе ,является весом петли сигнального графа; если константы нет , то весом является оператор (P).
Z1(P-2)= 0,5Z2+5Z3+Z4-6X;
Z2(P+0,1)= -0,5Z1+0,5Z5;
Z3(P-3,2)= Z4-0,3Z5+0,1X;
Z4(P+0,1)= Z5+0,1X+3,2Z3;
Z5(P+9)= 9Z1+0,5Z2+0,6Z4-0,6X;
Y=0,25Z1+0,1Z2+Z5;
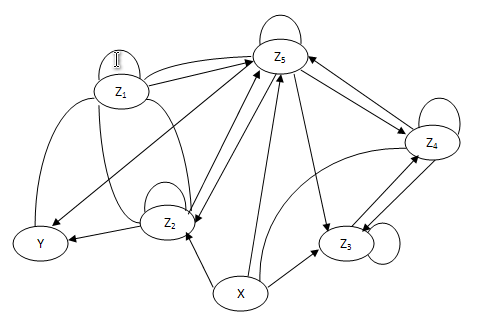
Далее алгоритм преобразования заключается в избавлении от петель, параллельных и последовательных дуг, а также от вершин , входящих в граф , за исключением вершин , которые являются входной и выходной величиной. Избавимся от петли на узле Z4:
A1=
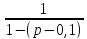 ;
A2=
;
A2=
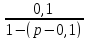 ;
а затем - от встречно параллельных дуг:
;
а затем - от встречно параллельных дуг:
A3=
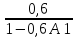 ;
A4=
;
A4=
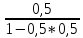 ;
;
Избавляемся от петли на узле Z2:
A5=
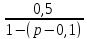 ;
A6=
;
A6=
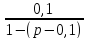 ;
;
A7=
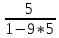 ;
A4=
;
A4=
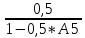 ;
;
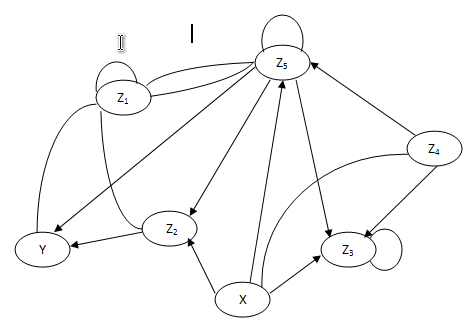
Избавляемся
от Z1 :
A9=
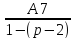 ;
;
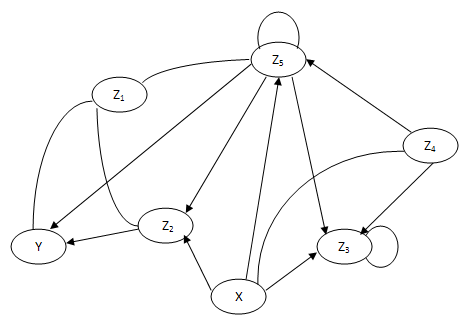
Избавимся
от Z5:
A10=
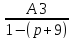 ;
A11=
;
A11=
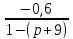 ;
;
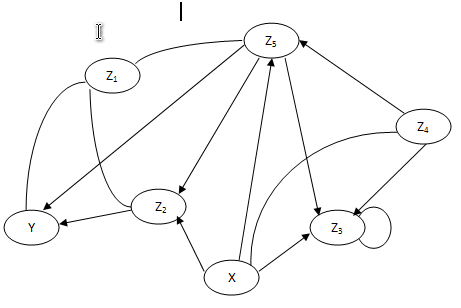
Избавимся от узла Z4 , при этом каждую вхдящию дугу уничтожают на все входящии дуги
При этой вершине : A12=A2*A10; A13=A2*1
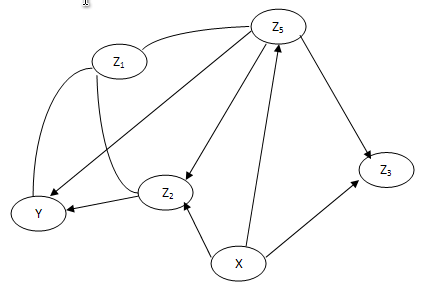
Избавимся от паралельных дуг : A14= -0,2+A13 и от петли на вершине Z3:
Z3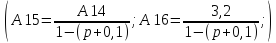 Если в
графе
существует
вершина , которая имеет только входящии
дуги и не выходящии , такая вершина
называется стоком и от неё можно
избавиться без каких либо изменений в
графе. Такой вершиной является Z3,
следовательно
от нее избавляемся.
Если в
графе
существует
вершина , которая имеет только входящии
дуги и не выходящии , такая вершина
называется стоком и от неё можно
избавиться без каких либо изменений в
графе. Такой вершиной является Z3,
следовательно
от нее избавляемся.
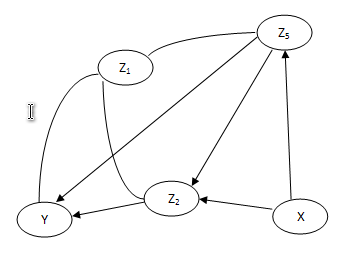
Избавляемся от узла Z1: A17=A9*A8; A18=A9*0,25;
И исключаем все паралельные дуги : A19=1+A18; A20=A4+A17; A21=A11+A12;
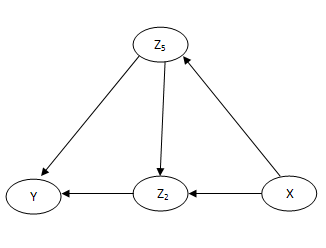
Избавляемся от узла Z2: A22=2*A6; A23=A6*A20;
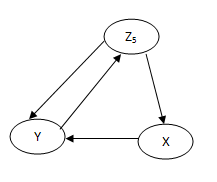
Избавимся от Z5; A24=A19+A23 ; A25=A21*A24; A26=A22+A25;
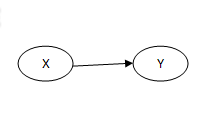
Задание № 2
По заданным схемам ориентированного и неориентированного графов составить матрици
смежности и инцендентности , а также провестиоптимизациюграфов.
Неориентированный граф.
a
1 b

7 3
4 4

5 e 5
d c
Составляем список ребер в порядке в порядке увеличения их весов:
(a,b),(e,b),(a,d),(b,c),(e,c),(a,c),(d,c).
Далее отбрасываем ребра образующие цикл:
(a,b),(a,d),(e,d),(e,b)
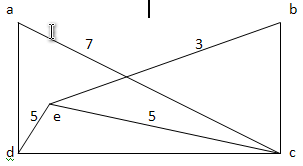
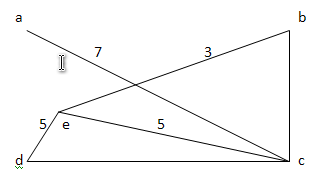
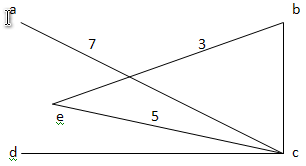
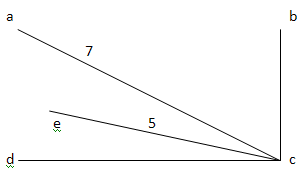
Составим матрицы смежности и инциндентности.
|
A= |
|
a |
b |
c |
d |
e |
|
a |
0 |
1 |
1 |
1 |
0 |
|
|
b |
1 |
0 |
1 |
0 |
1 |
|
|
c |
1 |
1 |
0 |
1 |
0 |
|
|
d |
1 |
0 |
1 |
0 |
1 |
|
|
e |
0 |
1 |
1 |
1 |
0 |
Инциндентности
|
B= |
|
ab |
bc |
cd |
de |
ae |
ac |
be |
bd |
|
a |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
b |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
c |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
d |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
e |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
Ориентированный граф.
5 
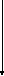

7 1 6
1
13 

1
Минимальный путь от истока к стоку – последовательность вершин .
[0-X1-X2-X3-X4]
. Вес пути F=5+1+1+1=8
Состовляем матрици смежности и инциндентности.
|
R= |
|
0 |
X1 |
X2 |
X3 |
X4 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
|
X1 |
0 |
0 |
0 |
1 |
1 |
|
|
X2 |
0 |
0 |
0 |
1 |
1 |
|
|
X3 |
0 |
0 |
0 |
0 |
1 |
|
|
X4 |
0 |
0 |
0 |
0 |
0 |
|
S= |
|
0 X1 |
X1 X2 |
X2X3 |
0 X2 |
X1X4 |
X3X4 |
|
0 |
-1 |
0 |
0 |
-1 |
0 |
0 |
|
|
X1 |
+1 |
-1 |
0 |
0 |
-1 |
0 |
|
|
X2 |
0 |
+1 |
-1 |
+1 |
0 |
0 |
|
|
X3 |
0 |
0 |
+1 |
0 |
0 |
-1 |
|
|
X4 |
0 |
0 |
0 |
0 |
+1 |
+1 |
Вывод: Я ознакомился с математическим описанием САУ с помощью графов и составления графов , а также оптимизации ориентированных и неориентированных графов и составления матриц смежности и нциндентности.
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖИНЕРНО – СТРОИТЕЛЬНЫЙ
КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ
по практической работе № 3.
Математическое описание объектов или
систем с помощью графов
По дисциплине: «Математические основы теории систем».
Выполнил
Принял
Балаково 2008
