практическая работа / Классический спектральный анализ лаба 8

 Классический спектральный анализ

 

Совокупность коэффициентов и при разложении периодической функции в ряд Фурье называются частотными спектрами этой функции.

и являются зависимыми от номера гармоники k.

Графически частотные спектры изображаются в виде отрезков длины и перпендикулярно оси на которой откладываются значения либо , либо .

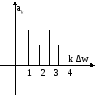
Расстояние между отдельными отрезками равно 1, если , и , если период равен .

Спектральный анализ - заключается в отображении совокупности коэффициентов разложения функции в ряд Фурье Также спектром временной зависимости (функции) f(t) называется совокупность ее гармонических составляющих, образующих ряд Фурье. Спектр можно характеризовать некоторой зависимостью А_k (спектр амплитуд) и j _k (спектр фаз) от частоты w _k = kw ₁.

 

Спектральный анализ периодических функций заключается в нахождении амплитуды А_k и фазы j _k гармоник (косинусоид) ряда Фурье (4). Задача, обратная спектральному анализу, называется спектральным синтезом.

Порядок выполнения лабораторной работы 8

 

Задание Вычислить первые шесть гармоник разложения в ряд Фурье функции f(t) на отрезке [0,2]. Построить графики всех гармоник. Выполнить классический спектральный анализ и синтез функции f(t) по шести гармоникам. Отобразить графически спектры амплитуд и фаз, результат спектрального синтеза функции f(t).

 

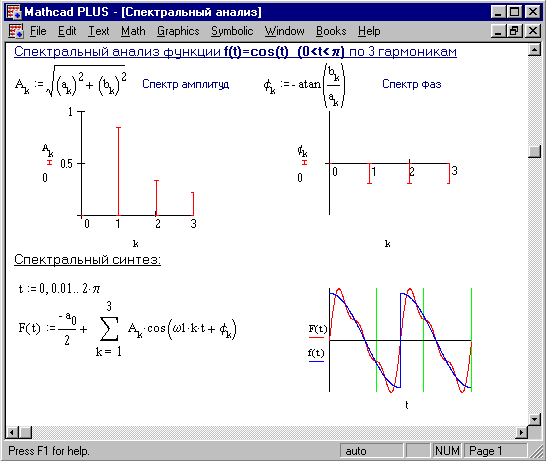
Рисунок 1. Классический спектральный анализ и синтез

 

Варианты задания 1

 

№ варианта	f(t)	№ варианта	f(t)	№ варианта	f(t)
1		6		11
2		7		12
3		8	cos e |sin 3 t|	13
4		9	cos t cos | sin t |	14
5	| sin t | + | sin 2t |	10		15	cos (sin t)

Вопросы контроля

1 спектры периодических функций

2 свойства спектров