Синтез не полностью заданных логических функций

По условиям работы логического устройства может оказаться, что некоторые наборы значений аргументов являются запрещенными для данного устройства и никогда не могут появляться на его входах. В этом случае функция оказывается заданной не на всех наборах аргументов. Такие функции будем называть не полностью заданными.

При синтезе логического устройства, реализующего не полностью заданную функцию, допустимо произвольно задаваться значениями функции на запрещенных наборах аргументов. При этом в заннсимости от способа задания этих значений функции минимальная фирма может оказаться простой или более сложной. Таким образом, возникает проблема целесообразного доопределения функции на запрещенных наборах аргументов.

Может быть использован следующий способ получения минимальной формы не полностью заданной функции f:

а) записывается СДПФ (СКИФ) функции f₀. полученной из f путем задания значения 0 (значения 1 и случае СНКФ) на всех запрещенных наборах аргументов;

б) записывается СДНФ (СКИФ) функции f₁, полученной из f путем задания значения 1 (значения 0 в случае СКНФ) на всех запрещенных наборах аргументов;

в) функция f₁ приводится к сокращенной форме (к форме, содержащей все простые имплнканты);

г) составляется импликантнзя таблица из всех членов функции f₀ и простых импликант функции f₁;

д) искомая минимальная форма составляется из простых импликант функции f₁, поглощающих все члены СДНФ (СКНФ) функции f₀.

Рассмотрим применение данного метода к минимизации не полностью заданной функции, приведенной в табл. 3.19,

Записываем логическое выражение функции f₀ в СДНФ

Записываем СДНФ функции f₁

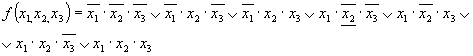
Методом Квайна приводим функцию f₁ к сокращенной форме:

Составляем импликантную таблицу (табл. 3.20).

Таблица 3.19
x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f(x1,x2,x3)	*	0	1	*	1	*	*	1

 

Таблица 3.20
Простые импликанты функции f1	Члены СДНФ
	X	X
	X		X
		X	X

 

Минимальная форма логического выражения функции может быть получена исключением любой из трех простых импликант

 

Рассмотрим минимизацию той же функции методом карты Вейча (табл. 3.21).

При минимизации функции данным методом следует на запрещенных наборах аргументов задавать функции такие значения, при которых клетки со значением 1 (либо 0) охватываются минимальным числом областей с максимальным числом клеток в каждой из областей. Применительно к рассматриваемся функции такое доопределение функции может быть осуществлено тремя различными способами, представленными в табл. 3.22. Они приводят к полученным выше выражениям МДНФ функции.

 

Синтез логических устройств с несколькими выходами

Пусть синтезируемое логическое устройство имеет п входов и т выходов (рис. 3.30). На каждом из выходов должна быть сформирована определенная функция входных переменных.

Эта задача могла бы быть решена синтезированием раздельно действующих узлов, каждый из которых реализовывал бы определенную выходную функцию. Однако, если даже каждый из этих узлов будет построен минимальным образом, в целом логическое устройство может оказаться не минимальным. Действительно, такое устройство могло бы быть подвергнуто минимизации путем использования общих элементов и нескольких устройствах, реализующих различные выходные функции.

Из этих соображений принеленне каждой из выходных функций к минимальной форме не является услонисм получения минимального в целом устройства. При минимизации устройств и целим некоторые нз функций могут оказаться представленными и неминимальной форме.

Принцип получения минимальной формы устройства сводится к нахождению минимального набора членов с минимальным числом входящих в них букв, достаточного для получения всех формируемых устройством функций.

Метод построения минимальных логических устройств с несколькими выходами рассмотрим на примере реализации устройства, способ функционирования которого задан табл. 3.23.

Записываем наборы аргументов, на которых хотя бы одна из выходных функций имеет значение 1, Рядом в таблице в качестве признака записываем функции, принимающие значения 1 при данном наборе аргументов (табл. 3.24).

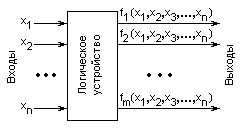
рис 3.24

Затем проводим операцию склеивания и получающиеся при этом члены заносим в табл. 3.25, рядом с членами записываем признаки в виде функций, общих в признаках той пары членов табл. 3.24, склеиванием которых они получены. Так склеивание членов табл. 3.24 и

Приводит в табл. 3.25 к члену ; склеивание членов

и приводит к и т. д.

Таблица 3.23
X1	0	0	0	0	1	1	1	1
X2	0	0	1	1	0	0	1	1
X3	0	1	0	1	0	1	0	1
f1(x1,x2,x3)	0	1	0	1	0	0	1	1
f2(x1,x2,x3)	0	0	1	0	1	1	0	0
f2(x1,x2,x3)	0	1	1	1	1	1	0	0

 

 

Таблица 3.25
	f1f3
	f3
	f3
	f1
	f2f3
	f1

Не проводится операция склеивания над членами, в признаках которых не имеется общих функций.

Далее проводится операция поглощения членами табл. 3.25 членов табл. 3.24. Операция поглощения может проводиться лишь над членами, имеющими одинаковую комбинацию функций в признаках.

Указанные операции склеивания и поглощения повторяются, пока их проведение оказывается возможным. Затем составляется импликантная таблица (табл. 3.26). Определяется набор импликант, обеспечивающий перекрятие всех столбцов импликантной таблицы. Этот набор импликант приведен в табл. 3.27.

Записываем логические выражения для выходных функций, составленные из этих импликант, в признаках которых содержатся заданные функции:

 

 

Таблица 3.26

f1

f3

f2

f3

f1

f3

f2

f3

f2

f3

f1

f1

(f2f3)

X

X

(f1f3)

X

X

X

X

(f3)

X

X

(f3)

X

X

(f1)

X

(f2f3)

X

X

X

X

(f1)

X

X

 

Легко убедиться, что выражение для функции не является минимальным. Минимальная для этой функции форма

Однако замена в выражении функции f₃ члена членом

невыгодна, так как член присутствует и в выражении f₂ и он должен быть сформирован для этой функции.

На рис. 3.31 приведена функциональная схема устройства, обеспечивающего заданное табл. 3.23 функционирование. Как нидно из схемы, ряд элементов участвует одновременно в формировании нескольких выходных функций.

рис 3.31