§21. Оператор .

Оператор набла – векторный дифференциальный оператор. Оператор набла можно ввести по-другому:

Часто знак суммы опускают (правило суммирования Эйнштейна).

Запишем условие ортонормированности рассматриваемого базиса:

Действия оператора набла:

1. Оператор набла действует на скалярную функцию F:

или

2. Оператор набла скалярно действует на векторную функцию :

3. Оператор набла векторно умножается на векторную функцию :

Кроме векторного и скалярного, есть ещё смешенное произведение векторов:

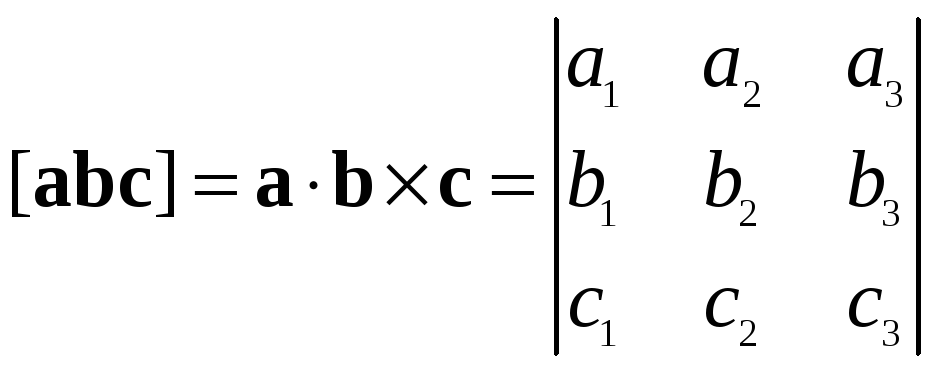- объем параллелепипеда.

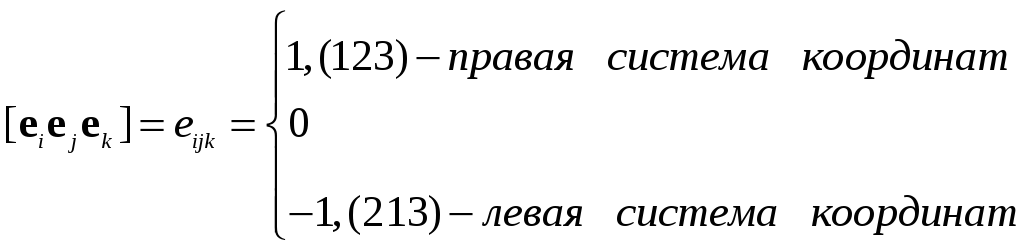
- единичный антисимметричный тензор третьего ранга.

Задачи

1. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

Решение.

2. Вычислить где p – постоянный вектор.

Решение.

§22. Уравнения Максвелла для электромагнитного поля в вакууме.

Будем использовать гауссову систему единиц.

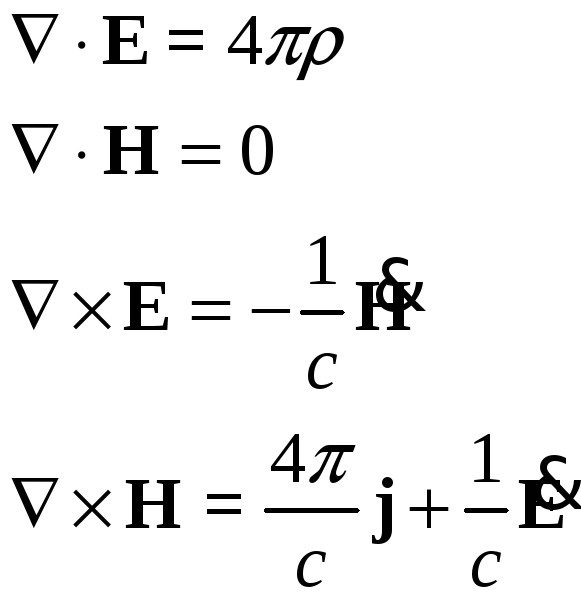
и являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.

§23. Потенциалы электромагнитного поля в вакууме.

Удобно ввести:

-векторный потенциал

-скалярный потенциал

однозначно определяют электромагнитное поле

§24. Градиентная инвариантность.

Существует преобразование, которое не меняет полевых характеристик . Таким преобразованием является градиентное:

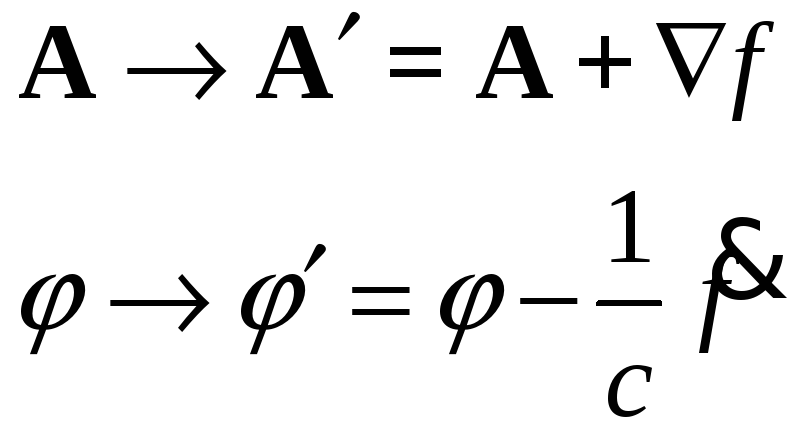
Здесь – произвольная функция координат и времени

-инвариантность полевых характеристик

относительно градиентных преобразований.

Аналогично для :

На потенциалы могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к. - произвольная.

§25*. -Функция.

Пусть имеется функция Хевисайда:

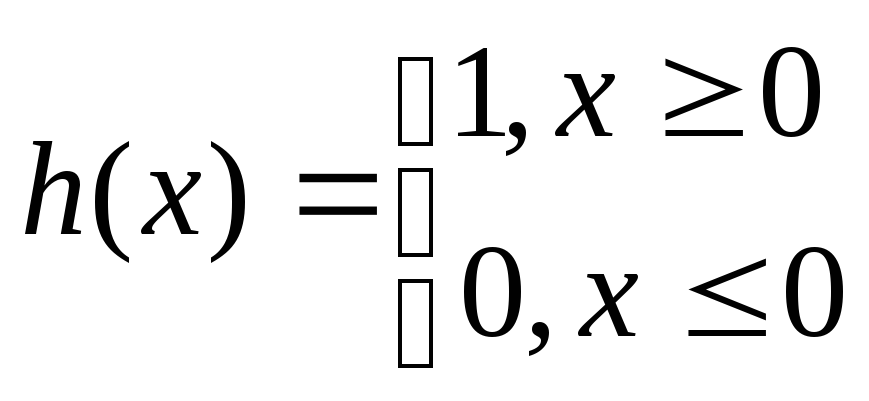
Ясно, что кроме , производная везде равна нулю. Рассчитаем интеграл:

, ,

Рассмотрим этот же случай, но картинка смещена на :

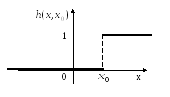
Интегральное одномерное соотношение:

Существует множество способов моделирования подобных функций.

Если , то (3) это :

Рассмотрим простейший случай.

- площадь под графиком функции:

Делим пополам.

И так далее до бесконечности. Это одна из простейших моделей -функции.

§26. Объёмная плотность точечного заряда.

Рассмотрим систему из точеченого заряда

Здесь возникает необходимость использовать -функцию.

Тогда:

Это соответствует случаю, когда заряд помещён в начало координат, а плотность заряда ищется в точке, с радиус-вектором .

Если же заряд помещён не в начало отсчёта, то плотность заряда перепишется в следующем виде:

В случае системы точечных зарядов имеем:

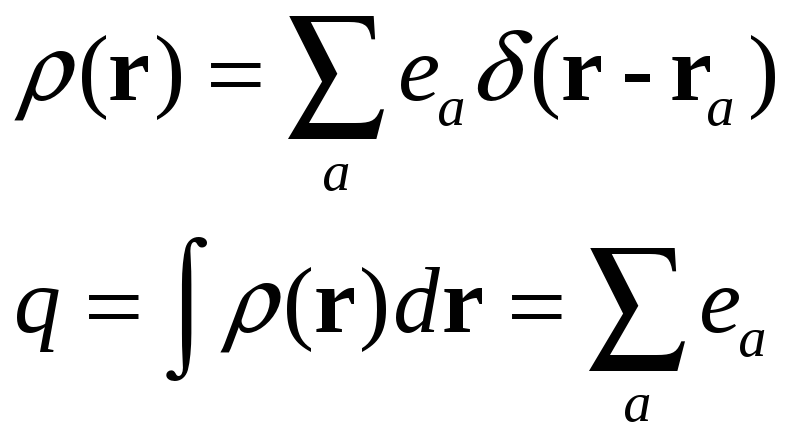
Для изображения плотности точечного источника всегда используется -функция.