§36. Условия квазистационарности поля.
1) Мы уже рассмотрели:
2) Характерные параметры линейного
проводника
характерных параметров поля
.
-
расстояние, на котором поле существенно
меняется за время
(если
пускаем волну, то
- длина волны; если изменение поля
гармоническое, то
- период).
3) Если длина пробега носителя тока –
электрона
,
то она гораздо меньше параметра поля
,
т.е.
.
4) Если носителями тока являются
перемещающиеся электроны, то вводим
характеристику
,
где
- длина пробега электрона, а
-
его скорость. Тогда:
3) и 4) позволяют записывать закон Ома
без учёта пространственно-временной
дисперсии, в простой форме:
.
§37. Глубина проникновения квазистационарного электромагнитного поля.
Уравнения Максвелла в случае квазистационарности:
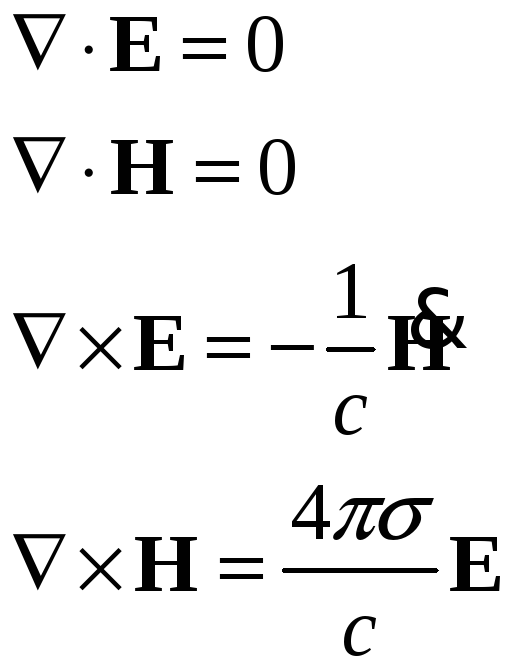
Здесь учтено, что
и
.
На два последних уравнения Максвелла
подействуем
:
- уравнение квазистационарного поля
Аналогично получаем для
:
Пусть
;
,
тогда:
где
Размерность
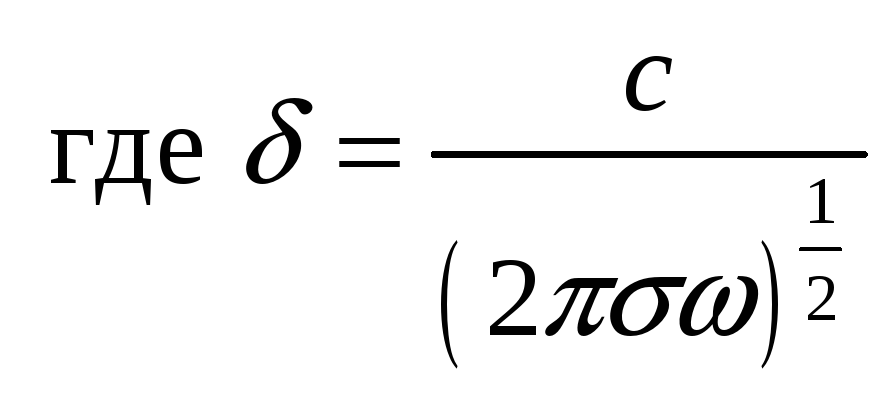- параметр глубины проникновения поля
.
Мы получили уравнение Гельмгольца:
Вид решения для
зависит от формы области, где ищется
решение. Если ищем в полуплоскости, то
- если взять
тогда получим
.
Это даёт граничное условие
Если взять
,
то это даст граничное условие
,
не объясняется ни физически, ни
подтверждается экспериментально. Таким
образом, следует брать
-параметр:
Для поля
аналогично:
- решение для полупространства.
Будем учитывать проникновение полей
и
только на глубину
,
т.к. дальше их проникновение мало и его
можно не учитывать, хотя оно существует.
§38. Уравнения Максвелла для электромагнитных волн в вакууме.
Нормальные электромагнитные волны в вакууме – это поля, которые могут существовать в отсутствии источников.
Будем рассматривать нормальные волны (т.е. без учёта источников). Уравнения Максвелла в вакууме имеют вид:
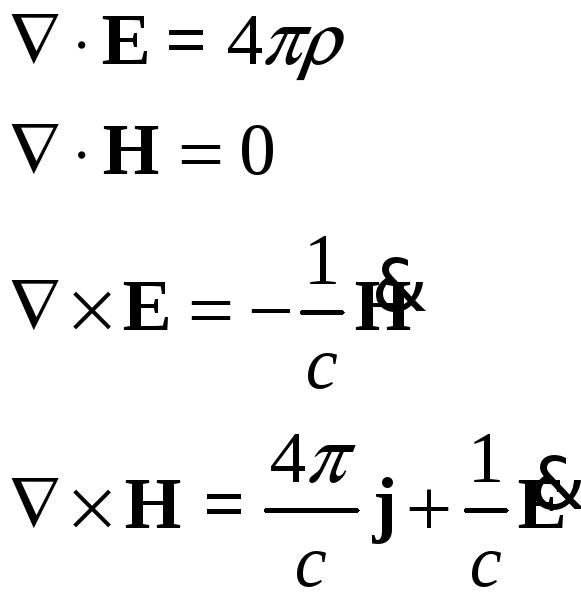
Величины
и
определяют свойства источников поля.
Нормальные волны существуют без
источников, тогда здесь уравнения
Максвелла:
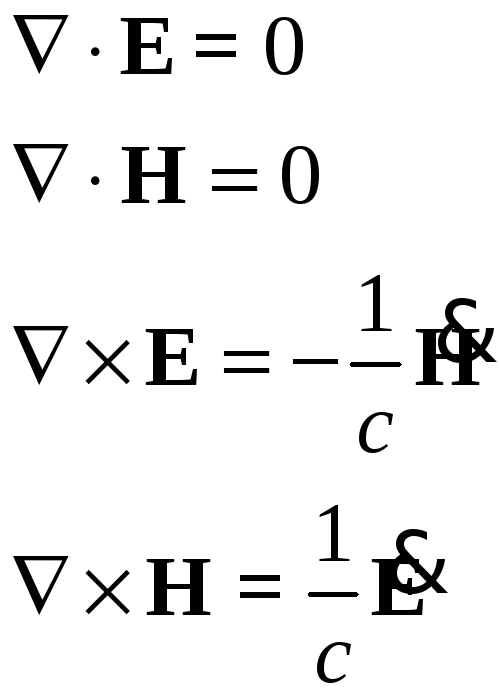
§39. Волновое уравнение в случае вакуума.
□
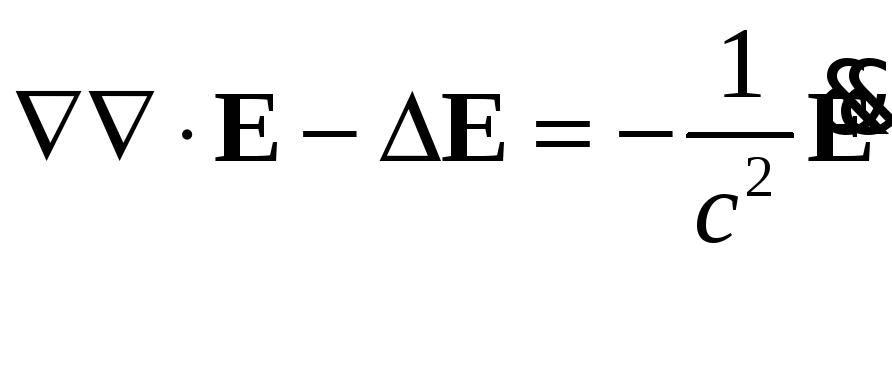
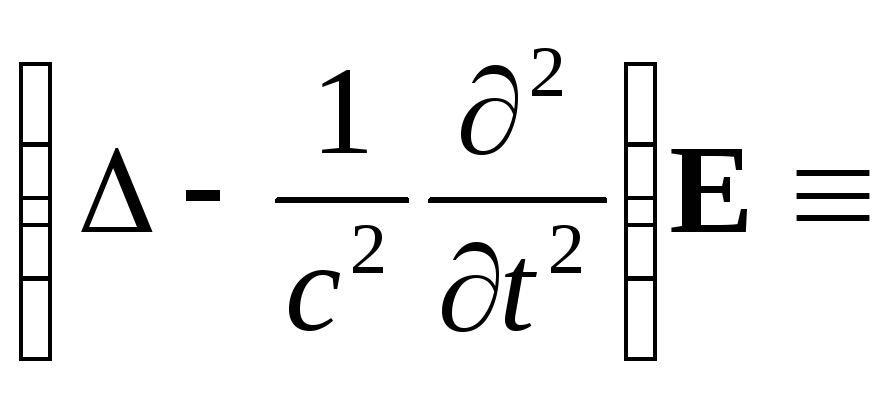Аналогично уравнение получаем для
:
□
Здесь будем использовать калибровку
поперечных волн (
),
т.к. в вакууме электромагнитные волны
плоские поперечные волны. Тогда:
§40*. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме.
Волновое уравнение для
:
Где
- это различные компоненты векторов
.
Волна плоская, т.к. фронт распространения волны представляет собой плоскость.
Имеем систему координат, точку на фронте
волны
,
нормаль к фронту волны
.
Тогда уравнение фронта волны (т.е.
плоскости ):
.
Но т.к. эта плоскость движется, то
появляется зависимость от времени.
Если фронт волны- сфера, т.е. волна
сферическая, то уравнение фронт а волны
и:
Учтём обстоятельство, что форма фронта
волны налагает на
некоторые
ограничения. Введём некоторые
вспомогательные координаты:
И будем упрощать оператор □
.
Можно перейти от (
)
к (
).
Рассчитаем
и
,
где функция
-
сложная.
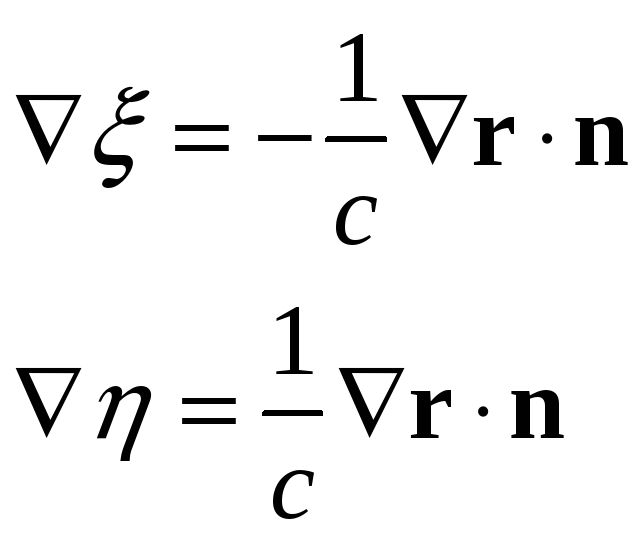
Рассмотрим компоненту:
.
Тогда:
Следовательно:
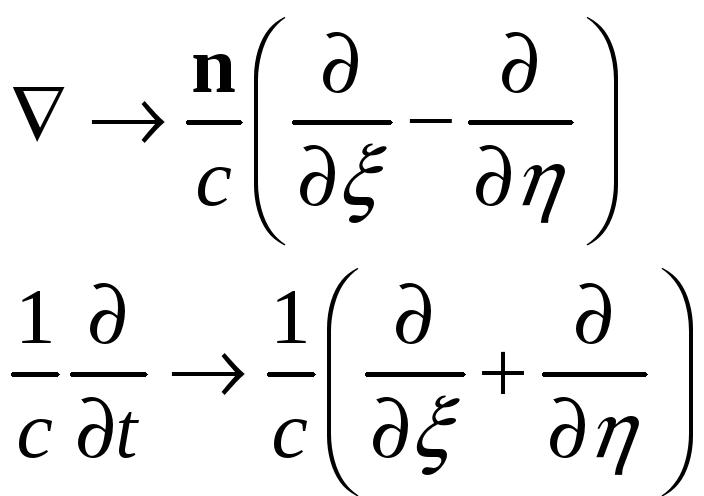
Это для случая плоской монохроматической волны. В результате имеем:
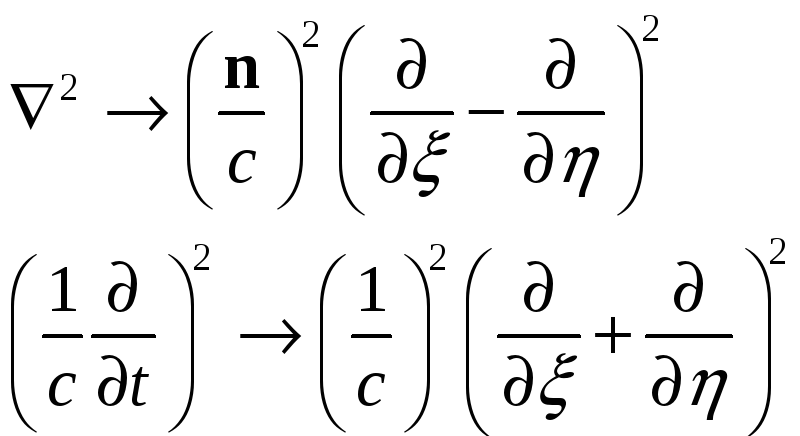
Тогда оператор □
Итак, □
,
тогда
.
где
.
Следовательно,
Тогда
,
где
и
Выясним, как происходит движение фронтов волны для 1 и для 2 случаев:
1 случай:
,
(*)
Получили, что фронт волны перемещается. Продифференцируем (*) по времени:
где
- фазовая скорость. Тогда
.
Для среды
,
для вакуума
,
тогда
.
Для вакуума
2 случай:
,
(**)
Продифференцируем (**) по времени:
-
фазовая скорость
И мы поучили, что фронт волны распространяется
в обе стороны. Если волна не встречает
препятствий, то решение -
и
,
иначе решение усложняется.