Система двух случайных величин
Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя числами. Такие величины называются двумерными.
Будем
обозначать через
двумерную случайную величину. Каждую
из величин
и
называют составляющей (компонентой);
обе величины
и ,
рассматриваемые одновременно, образуют
систему двух случайных величин.
Если
выборка состоит из набора двух случайных
величин
и
,
то набор точек с координатами
называется диаграммой
рассеивания.
Суммарное
квадратическое отклонение для линейной
регрессии
зависит от двух параметров
и
,
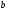и определяется соотношением:
.
(4)
Метод
наименьших квадратов для линейной
регрессии
заключается в нахождении «наилучших»
значений параметров
и
из условий минимума функции
,
то есть из системы уравнений:
(5)
Параболическая регрессия предполагает теоретическую зависимость
Теперь
суммарное квадратическое отклонение
зависит от трех параметров. Оптимальные
значения параметров находятся из условий
минимума функции
,
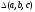то есть из системы трех уравнений.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсией составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
Корреляционным
моментом
случайных величин
и
называют
математическое ожидание произведения
отклонений этих величин. Для вычисления
корреляционного момента дискретных
величин используют формулу
Корреляционный момент служит для характеристики связи между величинами и .
Для
вычисления
часто используют следующую формулу:
.
(6)
Коэффициентом
корреляции
случайных величин
и
называют
отношение корреляционного момента к
произведению среднеквадратических
отклонений этих величин:
(7)
Он характеризует степень зависимости этих величин, причем не любой зависимости, а только линейной.
Практическая часть
Исходя из статистических данных (приведенных в таблице 1), построим кривую Филлипса, отражающую зависимость инфляции от безработицы.
|
Год |
Безработица, % |
Инфляция, % |
|
1990 |
-19,8 |
-129,4 |
|
1991 |
-2,3 |
-13,4 |
|
1992 |
-1,1 |
-8 |
|
1993 |
-19,2 |
-118,6 |
|
1994 |
-18,3 |
-113,3 |
|
1995 |
-20,1 |
-132,9 |
|
1996 |
-19 |
-119,9 |
|
1997 |
-21,5 |
-140,5 |
|
1998 |
-8,4 |
-46,3 |
|
1999 |
-21,1 |
-139,9 |
|
2000 |
-11,2 |
-63,8 |
|
2001 |
-10,1 |
-54,9 |
|
2002 |
-0,7 |
0 |
|
2003 |
-17,4 |
-106,4 |
|
2004 |
-11,2 |
-58,4 |
|
2005 |
-14,8 |
-90,8 |
|
2006 |
-15,1 |
-87,5 |
|
2007 |
-2,7 |
-14,6 |
|
2008 |
-9 |
-42,3 |
|
2009 |
-6,4 |
-31 |
Примем за X – безработицу, за Y – инфляцию.
1)Найдем для Х и У, математическое ожидание и дисперсию
|
|
|
|
Х |
Y |
|
Математическое ожидание |
-12,47 |
-75,595 |
||
|
Дисперсия |
|
48,3761 |
2188,668 |
|
2) Проведем статистический анализ данных для переменных X и Y. Найдем выборочные средние, дисперсии и среднеквадратические отклонения для X и Y по отдельности.
a) Для величин X и Y вычислим выборочные средние:
=
-12,47
=
-75,595
b) Найдем выборочные дисперсии и средние квадратические отклонения:
=
48,3761
Sx = 6,955293
=
2188,668
Sy = 46,78321
3) Найдем ковариацию Cov(X,Y):
Cov(X,Y) =323,39535
4) Найдем коэффициент корреляции X и Y.
Получим:
|
|
|
|
Х |
Y |
|
|
Математическое ожидание |
-12,47 |
-75,595 |
|||
|
Дисперсия |
|
48,3761 |
2188,668 |
||
|
Ср. квад. отклонение |
6,955293 |
46,78321 |
|||
|
Коэффициент корреляции |
0,993867189 |
||||
|
Выборочное среднее |
-12,47 |
-75,595 |
|||
|
Ковариация |
|
323,39535 |
|||
Выборочный коэффициент корреляции r служит для оценки силы линейной корреляционной связи: чем ближе |r| к единице, тем сильнее связь; чем ближе |r| к нулю, тем связь слабее. Видим, что в нашем случае линейная корреляционная связь сильная.
Так как выборочный коэффициент корреляции r положителен, то увеличение одной величины приводит к увеличению другой.
5) Найдем по выборке уравнение линейной регрессии (Y как функцию X) по методу наименьших квадратов.
Составим расчетную таблицу:
|
i |
Х |
Y |
XY |
X^2 |
Y^2 |
|
1 |
-19,8 |
-129,4 |
2562,12 |
392,04 |
16744,36 |
|
2 |
-2,3 |
-13,4 |
30,82 |
5,29 |
179,56 |
|
3 |
-1,1 |
-8 |
8,8 |
1,21 |
64 |
|
4 |
-19,2 |
-118,6 |
2277,12 |
368,64 |
14065,96 |
|
5 |
-18,3 |
-113,3 |
2073,39 |
334,89 |
12836,89 |
|
6 |
-20,1 |
-132,9 |
2671,29 |
404,01 |
17662,41 |
|
7 |
-19 |
-119,9 |
2278,1 |
361 |
14376,01 |
|
8 |
-21,5 |
-140,5 |
3020,75 |
462,25 |
19740,25 |
|
9 |
-8,4 |
-46,3 |
388,92 |
70,56 |
2143,69 |
|
10 |
-21,1 |
-139,9 |
2951,89 |
445,21 |
19572,01 |
|
11 |
-11,2 |
-63,8 |
714,56 |
125,44 |
4070,44 |
|
12 |
-10,1 |
-54,9 |
554,49 |
102,01 |
3014,01 |
|
13 |
-0,7 |
0 |
0 |
0,49 |
0 |
|
14 |
-17,4 |
-106,4 |
1851,36 |
302,76 |
11320,96 |
|
15 |
-11,2 |
-58,4 |
654,08 |
125,44 |
3410,56 |
|
16 |
-14,8 |
-90,8 |
1343,84 |
219,04 |
8244,64 |
|
17 |
-15,1 |
-87,5 |
1321,25 |
228,01 |
7656,25 |
|
18 |
-2,7 |
-14,6 |
39,42 |
7,29 |
213,16 |
|
19 |
-9 |
-42,3 |
380,7 |
81 |
1789,29 |
|
20 |
-6,4 |
-31 |
198,4 |
40,96 |
961 |
|
сумма |
-249,4 |
-1511,9 |
25321,3 |
4077,54 |
158065,5 |
Y=kx+b
Параметры k и b найдем по таким формулам:
; 
.
Получим:
|
k |
6,685023 |
|
b |
7,767239 |
Таким образом, линейная однопараметрическая модель регрессии показателя y от x имеет вид:
y(x) = 6,685023x+7,767239
6) Построим график, изображающий данные выборки и найденную функцию регрессии.
Нанесем линию регрессии на корреляционное поле.
7) Проверим гипотезу о значимости выборочного коэффициента корреляции при заданном уровне значимости альфа = 0.001.
Для проверки статистической значимости корреляционной зависимости величин воспользуемся критерием Стьюдента:
Для уровня значимости = 0,001 и числа степеней свободы равным 20–2 = 18 по таблице в учебнике, найдем критическое значение критерия Стьюдента t;(n–2) = t0,001; 18 = 3,92
Так как tрасчет > t(n–2) , то принимаем гипотезу Н. Вывод: корреляционная связь между признаками статистически значимая.
8) Соотношение между экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки. В таких случаях используют нелинейную (по объясняющей переменной) регрессию. Учитывая расположение точек корреляционного поля, предположим, что наиболее подходящим уравнением регрессии будет уравнение параболы
Его параметры b0, b1, b2 найдем, применяя метод наименьших квадратов:
Приравняв
частные производные
и
к
нулю, получим после преобразований
систему нормальных уравнений:
Для расчета необходимых сумм составим вспомогательную таблицу:
|
i |
Х |
Y |
X^2 |
X^3 |
X^4 |
YX |
YX^2 |
|
1 |
-19,8 |
-129,4 |
392,04 |
-7762,39 |
153695,4 |
2562,12 |
-50730 |
|
2 |
-2,3 |
-13,4 |
5,29 |
-12,167 |
27,9841 |
30,82 |
-70,886 |
|
3 |
-1,1 |
-8 |
1,21 |
-1,331 |
1,4641 |
8,8 |
-9,68 |
|
4 |
-19,2 |
-118,6 |
368,64 |
-7077,89 |
135895,4 |
2277,12 |
-43720,7 |
|
5 |
-18,3 |
-113,3 |
334,89 |
-6128,49 |
112151,3 |
2073,39 |
-37943 |
|
6 |
-20,1 |
-132,9 |
404,01 |
-8120,6 |
163224,1 |
2671,29 |
-53692,9 |
|
7 |
-19 |
-119,9 |
361 |
-6859 |
130321 |
2278,1 |
-43283,9 |
|
8 |
-21,5 |
-140,5 |
462,25 |
-9938,38 |
213675,1 |
3020,75 |
-64946,1 |
|
9 |
-8,4 |
-46,3 |
70,56 |
-592,704 |
4978,714 |
388,92 |
-3266,93 |
|
10 |
-21,1 |
-139,9 |
445,21 |
-9393,93 |
198211,9 |
2951,89 |
-62284,9 |
|
11 |
-11,2 |
-63,8 |
125,44 |
-1404,93 |
15735,19 |
714,56 |
-8003,07 |
|
12 |
-10,1 |
-54,9 |
102,01 |
-1030,3 |
10406,04 |
554,49 |
-5600,35 |
|
13 |
-0,7 |
0 |
0,49 |
-0,343 |
0,2401 |
0 |
0 |
|
14 |
-17,4 |
-106,4 |
302,76 |
-5268,02 |
91663,62 |
1851,36 |
-32213,7 |
|
15 |
-11,2 |
-58,4 |
125,44 |
-1404,93 |
15735,19 |
654,08 |
-7325,7 |
|
16 |
-14,8 |
-90,8 |
219,04 |
-3241,79 |
47978,52 |
1343,84 |
-19888,8 |
|
17 |
-15,1 |
-87,5 |
228,01 |
-3442,95 |
51988,56 |
1321,25 |
-19950,9 |
|
18 |
-2,7 |
-14,6 |
7,29 |
-19,683 |
53,1441 |
39,42 |
-106,434 |
|
19 |
-9 |
-42,3 |
81 |
-729 |
6561 |
380,7 |
-3426,3 |
|
20 |
-6,4 |
-31 |
40,96 |
-262,144 |
1677,722 |
198,4 |
-1269,76 |
|
сумма |
-249,4 |
-1511,9 |
4077,54 |
-72691 |
1353982 |
25321,3 |
-457734 |
Теперь система примет вид:
Решая систему методом Крамера, получим
b0 = -16,039
b1 = 0,314825
b2 = -0,27286
Тогда уравнение нелинейной регрессии имеет вид:
y = -16,039+0,314825x-0,27286x2
Добавим график функции y = -16,039+0,314825x-0,27286x2 на корреляционное поле.
Квадратичной регрессией и будет наша искомая кривая Филлипса.