лекции / логические элементы

Конъюнкция – логическое умножение

Дизъюнкция – логическое сложение

Элемент Шеффера, И-НЕ

,

Элемент Пирса, ИЛИ-НЕ

,

Элемент неравнозначности

, ,

Элемент И-ИЛИ-НЕ

RS – триггер на элементах И-НЕ

Временная диаграмма:

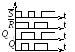
Построение RS – триггера на ИЛИ-НЕ элементах

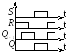
Счетные триггеры

Схема асинхронного, двухтактного T – триггера:

Синхронный T – триггер

Строится на базе двухтактных RS – триггерах.

D – триггер (триггер с задержкой по времени)

JK – триггер (универсальный)

Функциональная схема трехразрядного параллельного регистра, на базе однотактных D – триггерах.

Трехразрядный, параллельный, парафазный регистр на синхронном RS – триггере

Пример передачи кода слова между двумя, двухразрядными, параллельными и парафазными регистрами.

Трехразрядный последовательный сдвигающий регистр построенный на синхронных D – триггерах

Двухразрядный реверсивный сдвигающий регистр

Универсальный последовательный параллельный регистр (5 элементов 2-И-ИЛИ, 4 синхронных D – триггера)

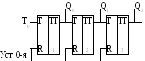
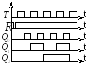
Трехразрядный суммирующий счетчик с последовательным переносом

Трехразрядный вычитающий счетчик с последовательным переносом

Трехразрядный реверсивный счетчик на двухтактных T – триггерах, и еще два элемента И-ИЛИ.

Реверсивный счетчик со сквозным переносом

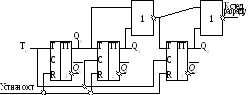
Ч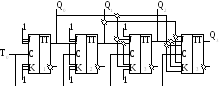 етырехразрядный суммирующий счетчик с последовательным переносом

1 2-ти разрядный счетчик со сквозным переносом

Ф ункциональная схема трехразрядного кольцевого счетчика на JK – триггерах.

ЗУ с непосредственной адресацией

Алгоритм работы устройства

Сверх оперативное ЗУ с непосредственной адресацией

Данная ЗУ строится на основе регистра:

Ассоциативные ЗУ

СОЗУ с ассоциативной адресацией

Функциональная схема комбинационного АЛУ магистрального типа

АЛУ накапливающего типа

Функциональная схема АЛУ для сложения чисел с ф.з.

АЛУ для сложения или вычитания чисел с ф.з.

АЛУ для умножения чисел с ф.з.

• 1-й способ: Умножение начинается с младших разрядов множителя, и сдвиге суммы частичных произведений вправо, при этом регистр множимого является неподвижным.

• 2-й способ: Умножение начинается с младших разрядов множителя, при неподвижной сумме частичных произведений, и сдвиге регистра множимого влево.

• 3-й способ: Умножение начинается со старшего разряда множителя при неподвижном множимом, и сдвиге суммы частичных произведений влево.

• 4-й способ: Умножение начинается со старших разрядов множителя при неподвижной суммы частичных произведений и сдвигом множимого вправо. РгМн и РгΣЧП имеют двойную длину относительно РгМт, при этом РгМт содержит цепи сдвига влево, а РгМн вправо.

Функциональная схема АЛУ для умножения чисел с ф.з. по методу 1

14